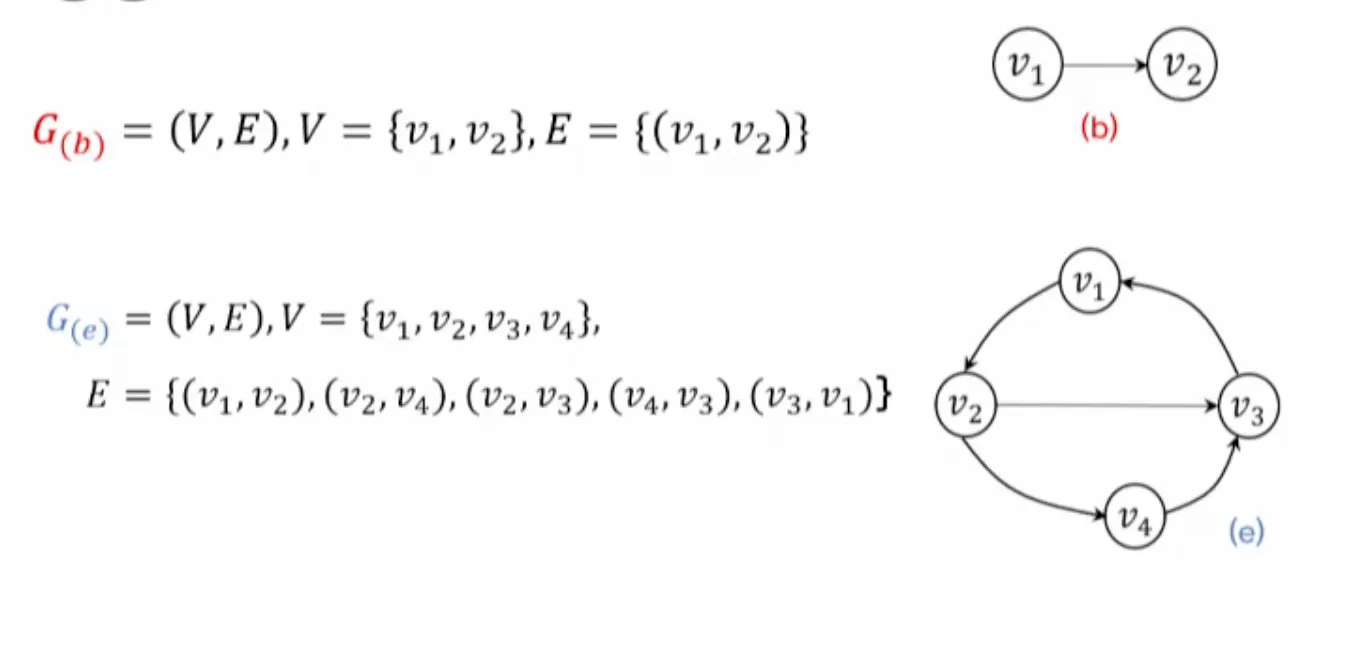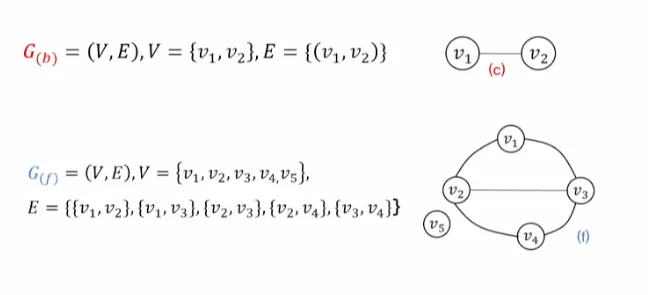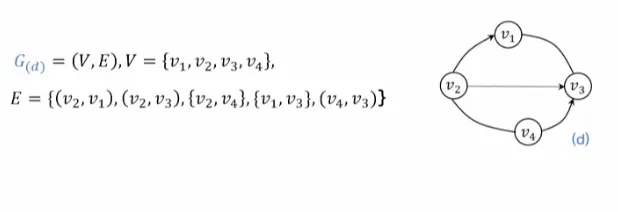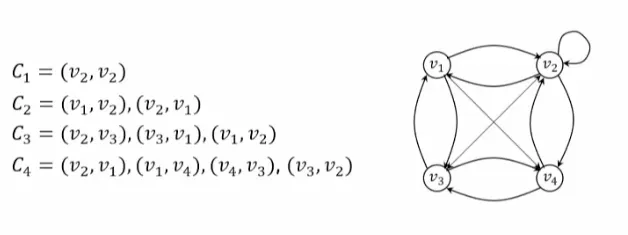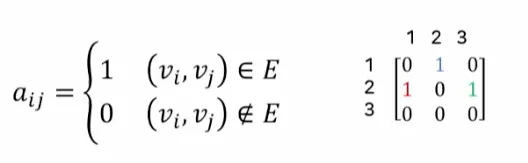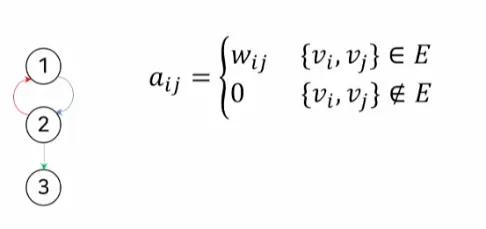1. 개념 및 용어
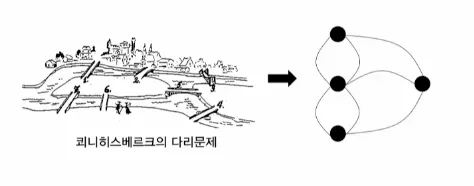
1.1. 그래프
•
"관계"를 그래프로 추상화하여 다룰 수 있음
•
전기회로의 분석, 최단 거리 탐색, 프로젝트 계획, 스케줄링, 운송, 컴퓨터 네트워크 등등
1.2. 그래프의 정의
•
구성
◦
그래프 G는 하나 이상의 정점(혹은 노드)을 포함하는 집합 V
◦
두 정점의 쌍으로 구성되는 간선을 포함하는 집합 E 의 순서쌍으로 정의함
•
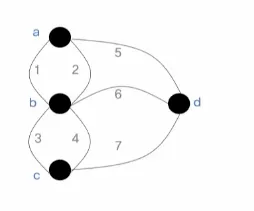
그래프 G = (V, E)
◦
V (정점의 집합) = { a, b, c, d}
◦
E (간선의 집합) = {1, 2, 3, 4, 5, 6, 7}
◦
G = ( V, E ) = ( { a, b, c, d}, {1, 2, 3, 4, 5, 6, 7 } )
1.3. 그래프의 용어 정리
•
간선
◦
두 정점을 연결하는 선
•
종류
◦
무방향 그래프 - 간선이 방향성이 없음
◦
방향 그래프 - 간선이 방향성이 있음
•
간선의 표현
◦
무방향 그래프의 간선 - 실선
◦
방향 그래프의 간선 - 화살표
•
간선은 두 정점 쌍으로 나타냄
◦
무방향 그래프의 간선
▪
정점 쌍이 순서를 나타낼 필요가 없음
▪
어떤 간선이 두 정점 v, v를 잇는 것이라면 {v, v}로 나타냄
◦
방향 그래프의 간선
▪
순서쌍 (v, v)로 표시함
1.4. 그래프의 연결
•
예시
◦
b,ㅎ : 방향
◦
c: 무방향
◦
d, f: 혼합
•
방향 그래프
•
무방향 그래프
•
혼합 그래프
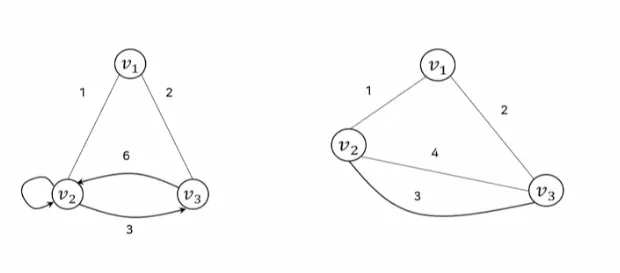
1.5. 다중 그래프
•
다중 그래프 : 두 정점을 잇는 간선이 여러 개인 그래프
◦
방향 다중 그래프 : 방향성을 갖는 간선으로 이루어진 다중 그래프
◦
무방향 다중 그래프 : 방향성이 없는 간선으로 이루어진 다중 그래프
1.6. 가중 그래프
•
간선이 가중치를 갖는 그래프
1.7. 그래프의 성질
•
무방향 그래프
◦
조합의 개수와 동일
◦
n 개의 정점을 갖는 무방향 그래프에서 vi ≠ vj 인 서로 다른 무순서쌍 { vi ,vj } 의 최대 개수
•
방향 그래프
◦
순열의 개수와 동일
◦
n 개의 정점을 갖는 방향 그래프에서 vi ≠ vj 인 서로 다른 무순서쌍 ( vi ,vj ) 의 최대 개수
•
완전 그래프 (Complete graph)
◦
모든 정점들이 간선으로 서로 연결된 그래프
◦
완전 그래프인 (만일 정점의 수를 n이라고 하면) 무방향 그래프의 간선 개수
•
두 정점 v와 v가 서로 인접한다
◦
무방향 그래프 간선 e ∈E가 {Vi ,Vj}으로 표현될 때,
즉,두 정점 Vi 와 Vj 를 연결하는 간선이 존재하는 경우를 말함
•
독립 정점
◦
다른 어떤 정점과도 인접하지 않은 정점
•
널(null)그래프
◦
독립 정점만으로 구성한 그래프이며, 간선의 집합 E는 공집합임
◦
정점만 있는 그래프 (간선이 존재하지 않는 그래프)
•
경로(path)
◦
임의의 두 정점을 연결하는 어떤 간선의 끝 정점(해당 간선의 머리)이 이어진 간선의 시작 정점(해당 간선의 꼬리)이 되는 간선의 열
◦
무방향 그래프 G
▪
(G)에 속하는 순서없는 간선 {Vp, V1}, {V1, V2},…, { Vn-1, Vn}, {Vn, Vq}가 있을 때,그래프 G 의 정점 Vp에서 Vq까지 경로는 정점 Vp, V1, V2 … , Vn, Vp들의 연속을 말함
◦
방향 그래프 G
▪
정점 Vp에서 Vq까지 경로는 (Vp, V1), (V1, V2), (V2, V3) … , (Vn-1, Vn), (Vn, Vq)로 구성됨
◦
특별한 언급이 없는 경우 정점 Vp에서 Vq까지의 경로는 Vp, V1, … Vn, Vq와 같은 경로상의 간선을 구성하는 정점 순서열로 표시함
◦
경로 길이
▪
경로에 있는 간선의 수
◦
단순 경로
▪
경로 상에 있는 모든 정점이 서로 다른 경로
•
A → B → C (O)
•
A → B → B → B → C (X)
◦
기본 경로
▪
경로 상에 있는 모든 간선이 서로 다른 경로
•
(A, B) (B, C) (C, D) (O)
•
(A, B) (B, B) (B, D) (X)
1.8. 방향 그래프
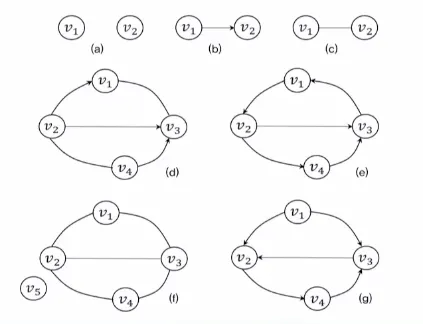
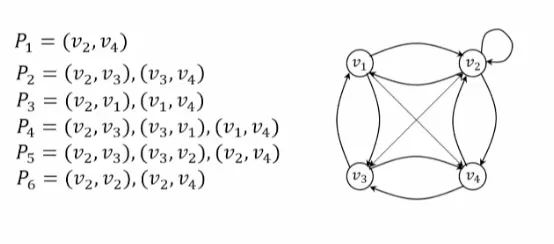
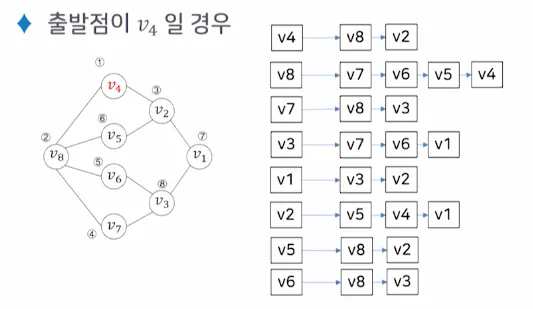
•
그래프의 정점 V2에서 출발하여 정점 V4에서 끝나는 경로
◦
단순경로: P1, P2, P3, P4
◦
사이클을 포함한 경로: P5, P6
•
사이클
◦
출발점과 도착점이 동일한 단순경로
◦
사이클 그래프
▪
사이클이 있는 그래프
1.9. 용어 정리
•
방향 그래프
◦
진입 차수: 주어진 정점으로 향한 간선의 개수
◦
진출 차수 : 주어진 정점에서 시작하는 간선의 개수
◦
정점의 차수 : 진출 차수와 진입 차수의 합
•
무방향 그래프
◦
차수: 정점에 연결된 간선들의 개수
•
루프
◦
간선의 시작점과 끝점이 같은 정점인 길이가 1인 경로
◦
cf) 길이가 1을 넘어서면 사이클 그래프
•
무사이클 그래프
◦
사이클이 없는 그래프를 ‘무사이클 그래프’ 혹은 ‘트리’ 라고 함
◦
방향이 있는 무사이클 그래프를 DAG(directed acyclicgraph)라고 부름)
1.10. 그래프와 트리의 차이
•
트리는 그래프의 부분집합
◦
트리는 그래프이다 (O)
◦
그래프는 트리이다 (X)
2. 추상 자료형
•
그래프 객체의 정의:정점과 간선의 유한 집합
•
연산
◦
GraphCreat() ::= 그래프 생성
◦
Destroy(Graph) ::= 그래프 기억장소 반납
◦
GraphCopy_Tree(Graph) ::= 그래프 복사
◦
InsertVertex() ::= 그래프에 정점 삽입
InsertEdge() ::= 그래프에 간선 추가
◦
DeleteVertex() ::= 정점 삭제
DeleteEdge()::=간선 삭제
◦
Search() ::= 정점 탐색
◦
IsAdjacent() ::= 인접 정점 여부 확인
◦
ExistPath() ::= 경로가 존재하는지 확인
◦
PathLength() ::= 경로 길이 계산
◦
BFS() ::= 너비 우선 탐색
◦
DFS() ::= 깊이 우선 탐색
3. 그래프의 표현 방법
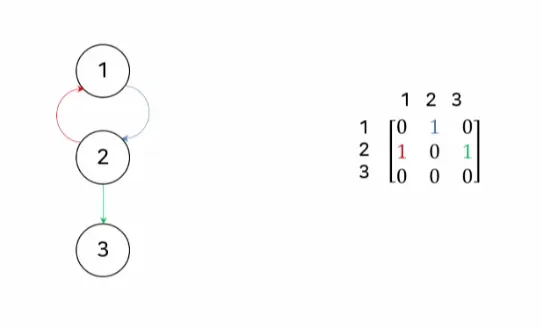
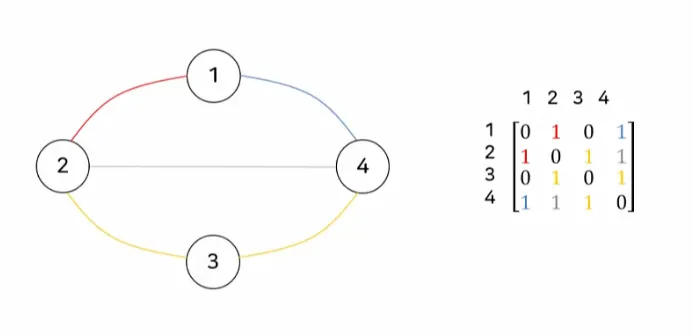
3.1. 인접 행렬
•
G = ( V, E)가 n개의 정점을 가진 그래프라고 가정함
•
그래프 G 는 n × n 행렬로 표현되고 다은과 같이 행렬값을 가짐
•
가중 그래프
◦
간선 { vi, vj} ( 방향 그래프라면 (vi, vj))의 가중치가 Wij일때, 인접행렬 요소 aij
는 아래와 같음
•
예시
◦
무방향 그래프는 대칭적인 구조를 띔
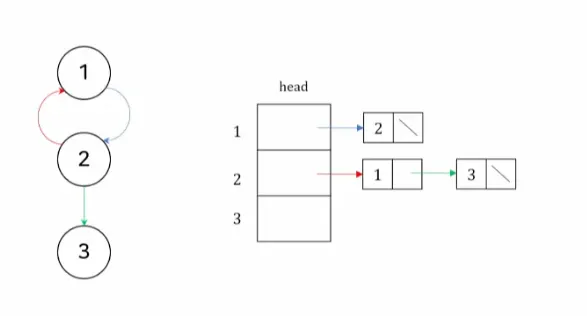
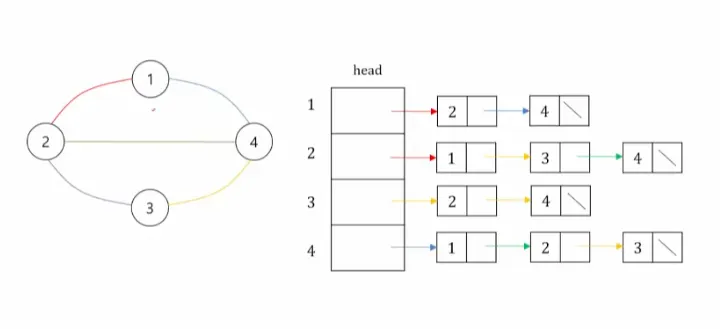
3.2. 인접 리스트
•
정점의 개수가 n인 그래프에 대하여,인접 행렬의 n행을 n개의 연결 리스트로 나타내는 방법
•
리스트 i 의 각 노드들은 정점 i 에 인접되어 있는 정점들을 나타냄
•
각 리스트 들은 헤드 노드를 가지며,헤드 노드들은 자신의 인접 정점을 순차적으로 가리키고 있음
•
예시
4. 그래프의 탐색
4.1. 정의
•
그래프에서 특정 정점을 찾는 기본 연산
•
그래프 G = (V, E)와 V(G)에 있는 정점이 v가 주어졌을 때, 정점 v 에 도달할 때까지 G의 정점을 방문하는 연산
◦
만일 없다면 그래프의 모든 정점을 방문한 후 종료함
•
그래프 순회 종류
◦
깊이 우선 탐색(DepthFirstSearch;DFS)
◦
너비 우선 탐색(BreadthFirstSearch;BFS) 두 가지 방법이 있음
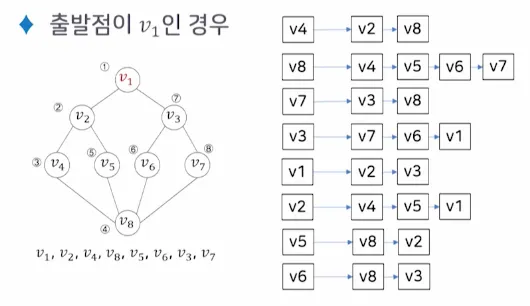
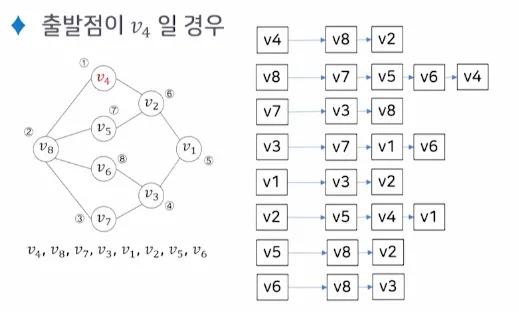
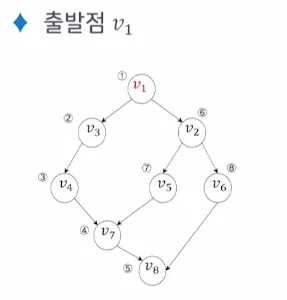
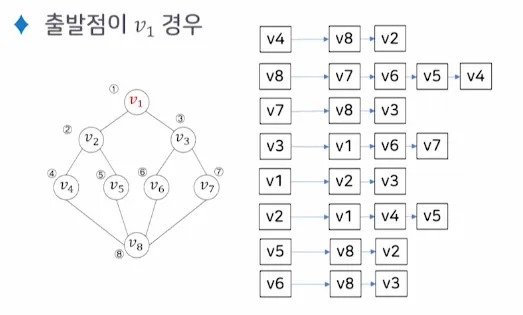
4.2. 깊이 우선 탐색 (DFS)
•
출발점 v 를 방문하는 것으로 시작
◦
다음으로 v 에 인접하고 아직 방문하지 않은 정점 w를 선택
◦
w를 출발점으로 다시 깊이 우선 탐색을 시작함
•
두 과정을 모든 정점을 한 번씩 방문 할 때까지 반복함
•
만약 인접한 모든 정점들이 이미 방문한 정점인 경우는 가장 최근에 방문했던 정점 중에서, 방문하지 않은 정점 w 를 가진 정점을 선택하여 정점 w 로부터 다시 깊이 우선 탐색을 시작함
•
미 방문 정점이 없으면 탐색을 종료함
•
DFS 무방향 그래프
•
DFS 방향 그래프
•
순환 호출
void DFS(int v){
int w;
extern int VISITED[];
VISITED[v] = 1;
while(v에 인접한 모든 정점 w)
if(!VISITED[w])
DFS(w);
}
C
복사
•
스택
void DFS(int v){
int n,w ;
extern struct stack *s;
extern int VISITED[];
InitializeStack(s);
push(s,v);
VISITED[v]=1;
while((n=pop(s))>=0){
VISITED[n]=1;
while(n에 인접한 모든 정점 w){
if(!VISITED[w]){
push(s,w); } } } }
C
복사
4.3. 너비 우선 탐색 (BFS)
•
출발점 v를 방문하는 것으로 시작함
◦
다음으로 v에 인접한 정점 w를 모두 방문
◦
다시 w에 인접한 방문하지 않은 정점들을 차례로 방문함
•
두 과정을 모든 정점을 한 번씩 방문할 때까지 반복함
•
너비 우선 탐색은 인접 정점을 모두 방문하기 때문에 스택이 필요하지 않고, 대신 큐를 사용함
5. 최소 신장 트리
5.1. 정의
•
트리: 사이클이 없는 단순 그래프 (한 정점에서 다른 정점으로 가는 경로가 유일한 독특한 구조)
◦
트리는 그래프
◦
루트를 가짐 - (일반 그래프에는 없는)계층 개념이 있음
◦
사이클 X
•
신장 트리(spanning tree)
◦
그래프 G의 모든 정점과 간선의 일부(또는 전부)를 포함하는 트리
◦
주어진 그래프의 정점을 모두 포함함
◦
사이클이 없음
◦
최소 n-1개의 간선으로 구성한 그래프
•
G 의 최소 부분 그래프
◦
그래프 G의 부분 그래프 중에서 간선의 수가 가장 작은 것
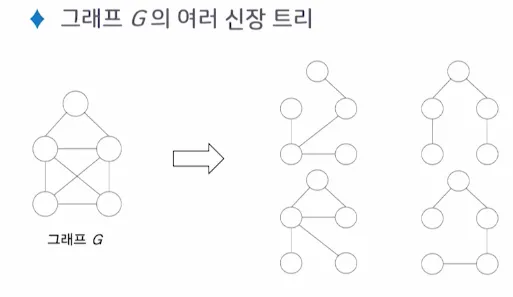
•
그래프 G의 여러 신장 트리
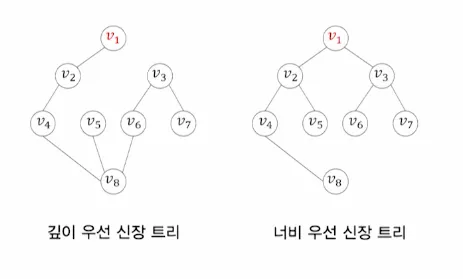
•
탐색 신장 트리
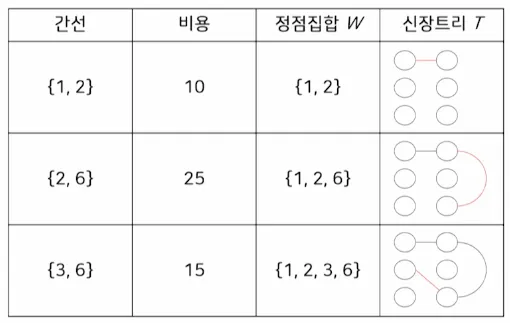
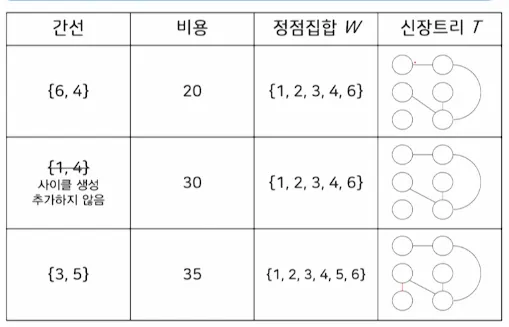
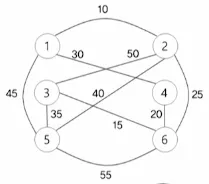
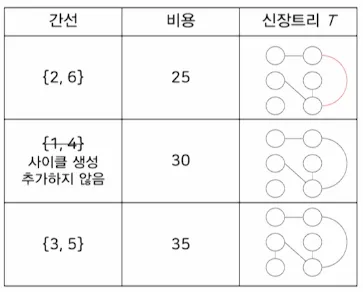
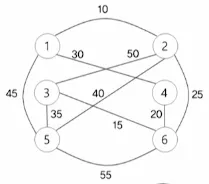
5.2. 프림(Prim) 알고리즘
•
n개의 정점을 갖는 연결 그래프 G에 대한 최소 비용 신장 트리 T를 구하는 알고리즘
•
그래프 전체에서 최소 비용을 갖는 간선 { u, v }를 선택하여 이 간선을 최소 비용 신장 트리 T에 추가함
•
이 간선을 최소 비용 신장 트리 T에 추가하였을 때 사이클을 형성하지 않으면 T에 추가하고 아니면 무시함
•
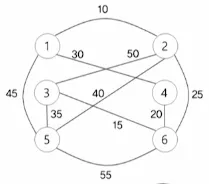
예시
•
소스 코드
void prim(){
T =φ;
W =φ;
E 로부터 최소 비용인 간선 { v, w }를 선택 ;
while(T는 n-1개 이하의 간선 포함 &&E는 공집합 아님){
E 에서 간선 {v, w}를 제거 ;
if({v, w}가 T 내에서 사이클을 생성 안함){
T = T ∪ v, w}}; //선택한 간선 추가
W = W ∪ v, w}; //선택한 정점 추가
}
else 간선 {v, w}를 버림 ;
E 로부터 W내의 정점과 최소 비용으로 연결된 간선 { v, w }를 선택 ; } }
C
복사
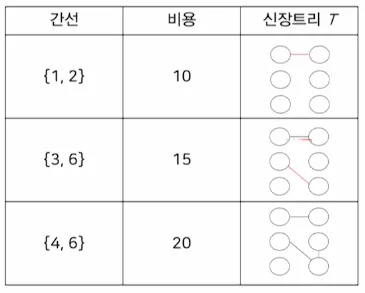
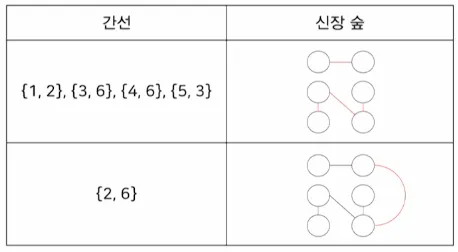
5.3. 크루스컬 알고리즘
•
남은 간선 중에서 무조건 최소 비용인 간선을 선택 한 후 사이클을 형성하지 않으면 그 간선을 선택함
•
중간 과정에 있는 T는 하나의 트리가 아니고 여러 개의 분리된 트리, 즉 숲일 수 있음
•
예시
•
소스 코드
void kruskal(){
while(T 가 n-1개 이하의 간선을 포함 && E 가 공집합 아님)
{
E 로부터 최소 비용인 간선 { v,w }를 선택;
E 에서 간선 { v,w }를 제거;
if({ v,w }가 T 내에서 사이클을 생성 하지 않음)
T = T ∪ v,w } };
else
간선 {v,w}를 버림; } }
C
복사
5.4. 솔린 (sollin) 알고리즘
•
간선이 하나도 없는 그래프의 모든 정점들로 구성된 숲에서 시작함
•
단계가 거듭되면서 숲 내의 트리들이 최소 비용을 갖는 간선으로 연결
•
예시