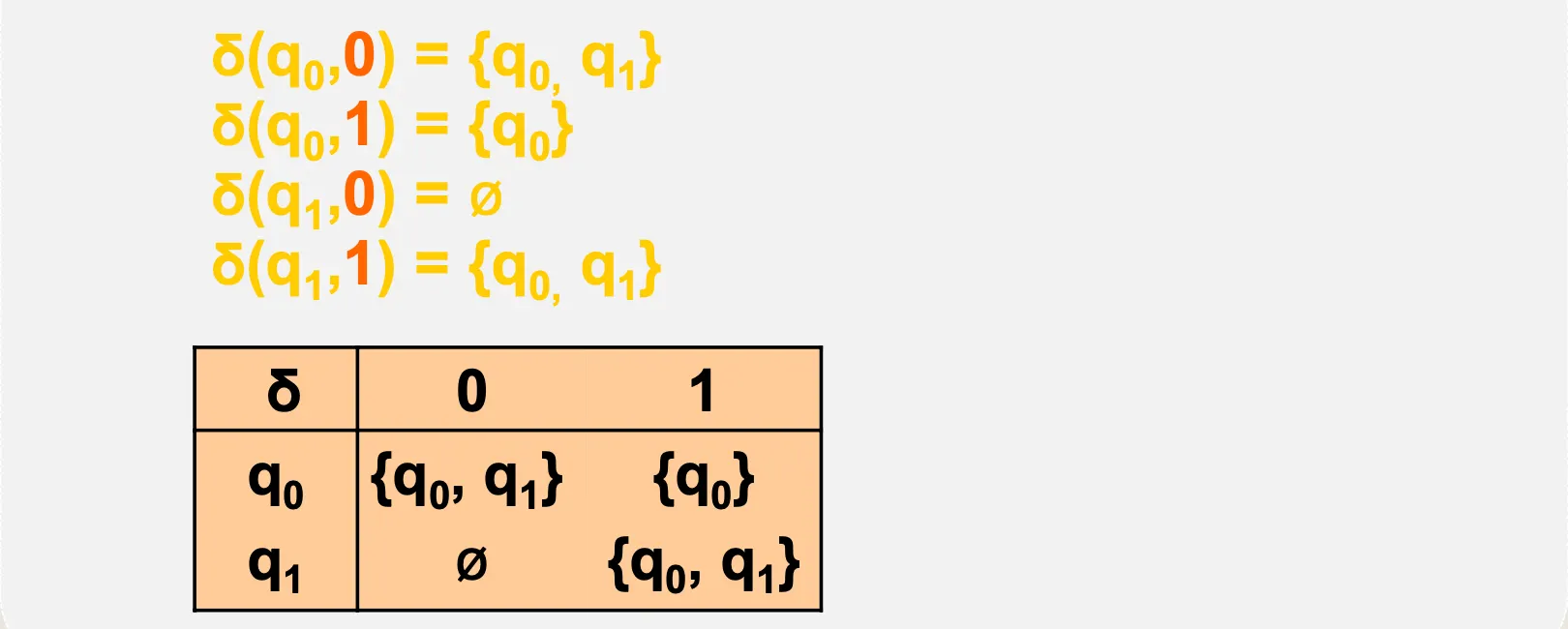Total
Search
1. 유한오토마타
1.1. 정의
•
프로그램 설계를 위한 수학적 모델
•
문자열이 언어의 문장인지 판단함
•
입력으로 문자열을 받아서 문자열이 그 언어의 문장이면 yes, 그렇지 않으면 no를 답하는 기능을 수행
1.2. 예시
•
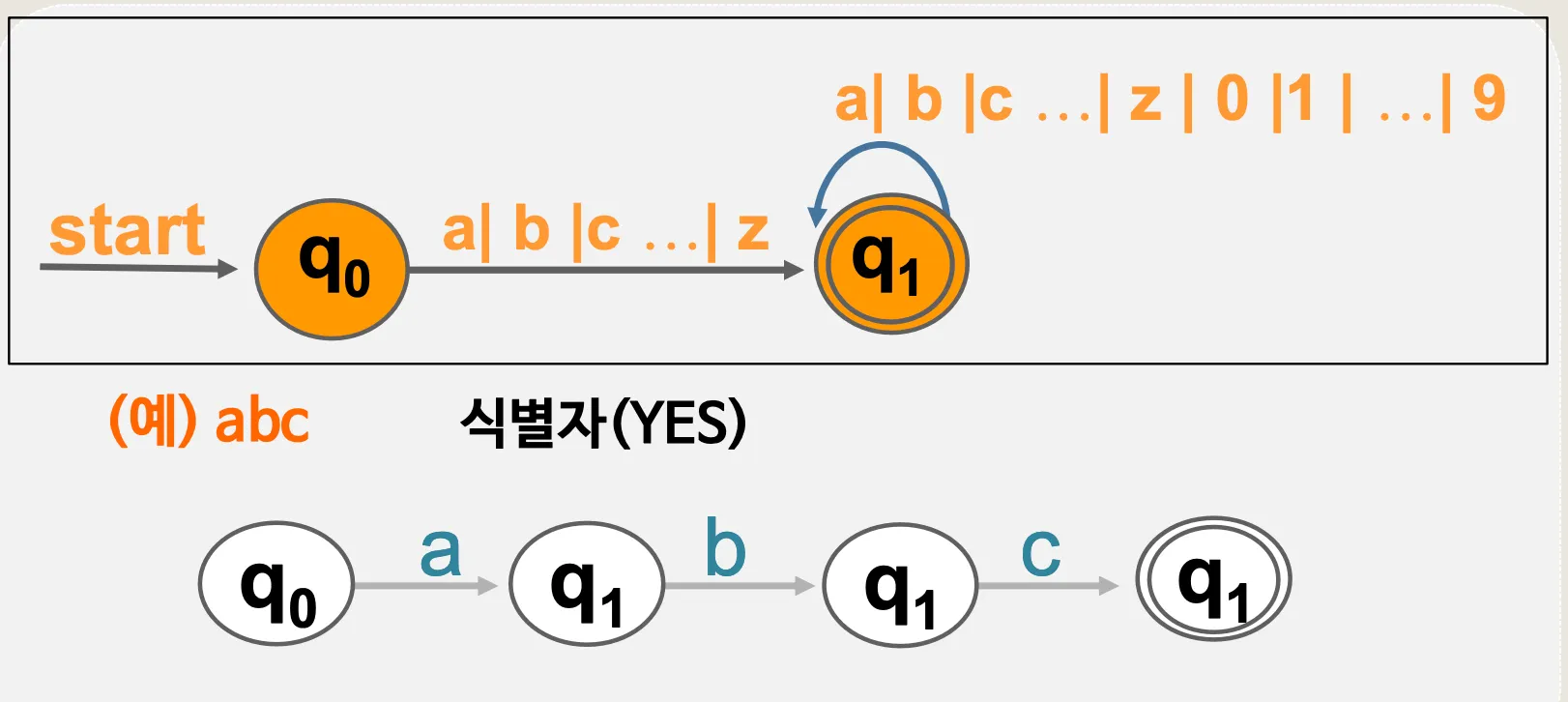
식별자 ABC := E * 3.14 + ABC / E;
1.
첫자는 영자
2.
다음부터 영자와 숫자의 조합
•
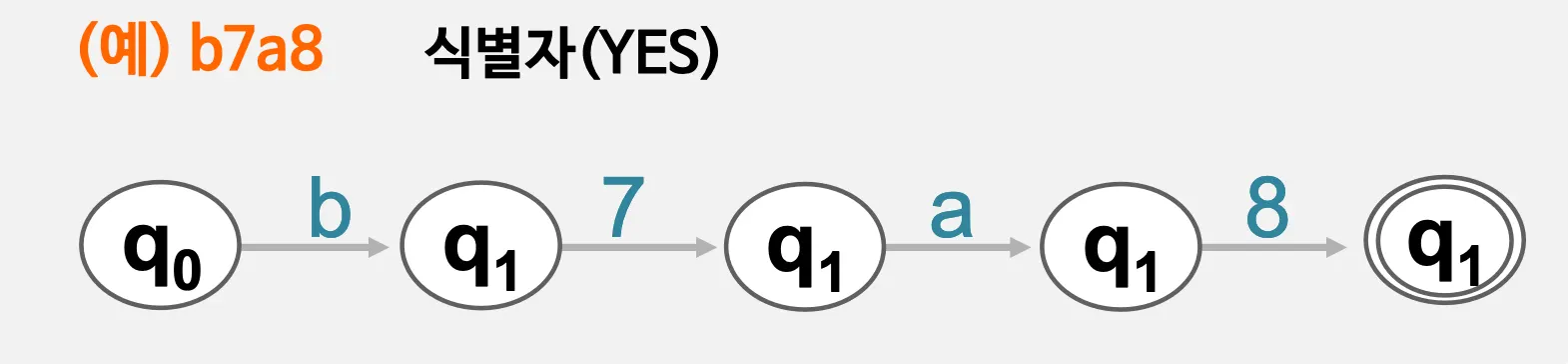
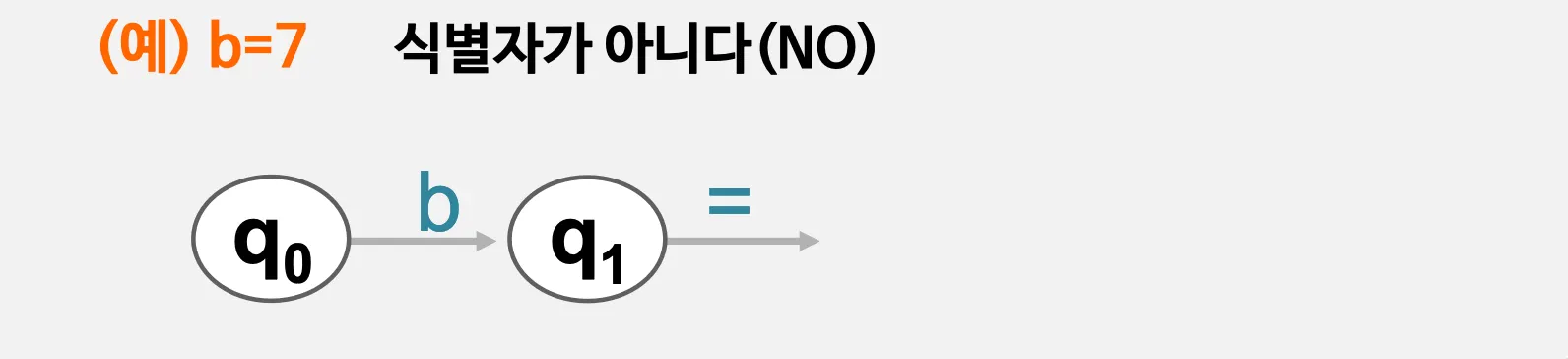
예시
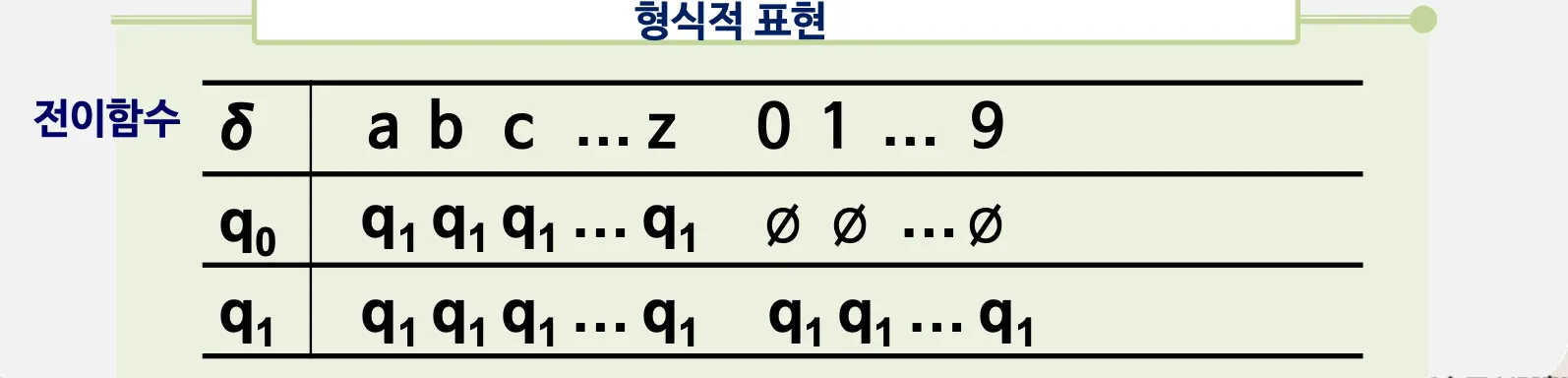
1.3. 유한오토마타의 형식적 표현
•
형식적 표현
◦
Q: 상태
◦
Σ: 입력기호
◦
q0: 시작상태
◦
F: 종료상태
2. 정규표현과 유한오토마타
2.1. 정규표현 → 유한오토마타
•
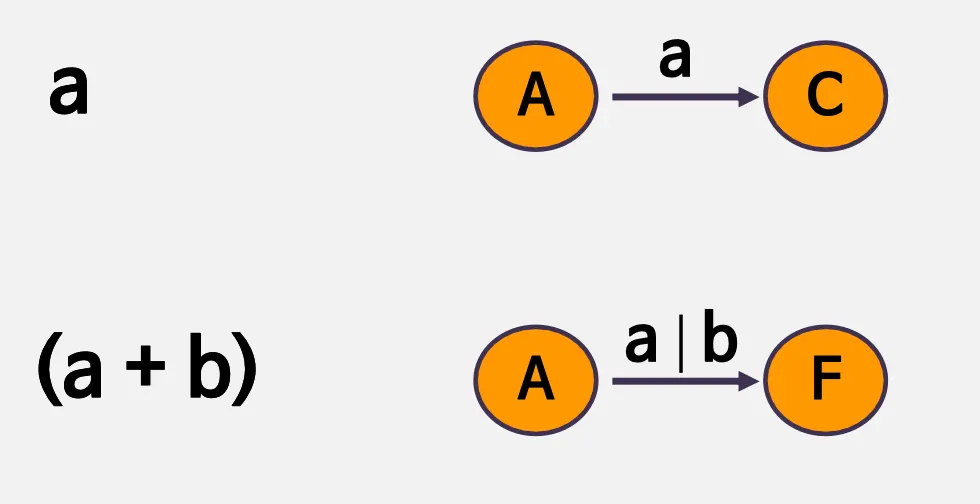
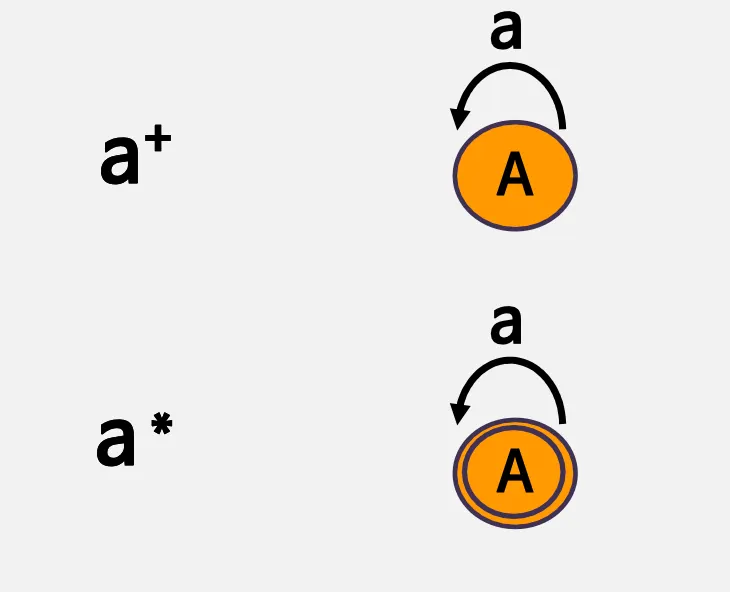
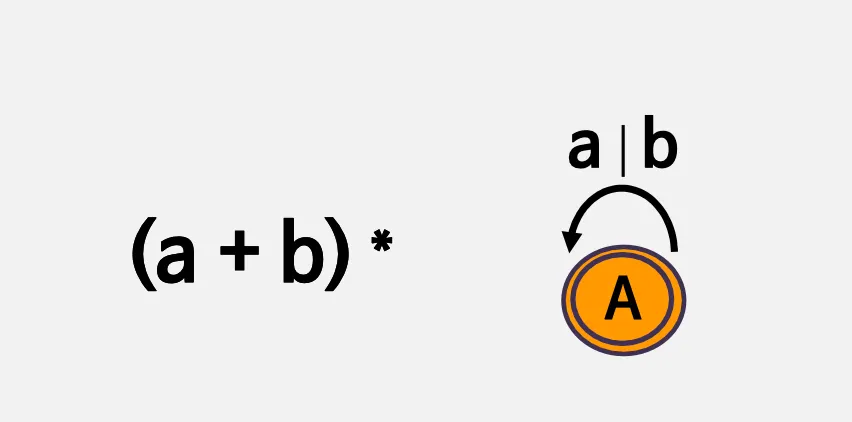
종류
a* 는 무한반복 가능하다는 것을 의미
a+는 종료가능
•
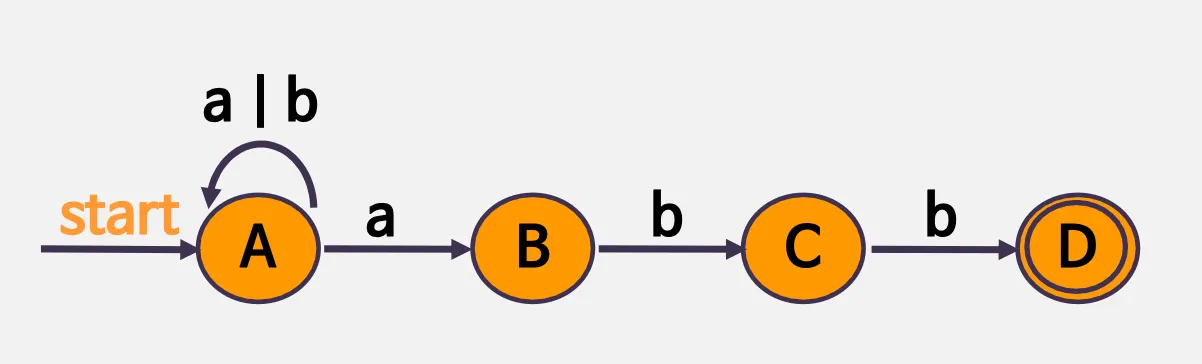
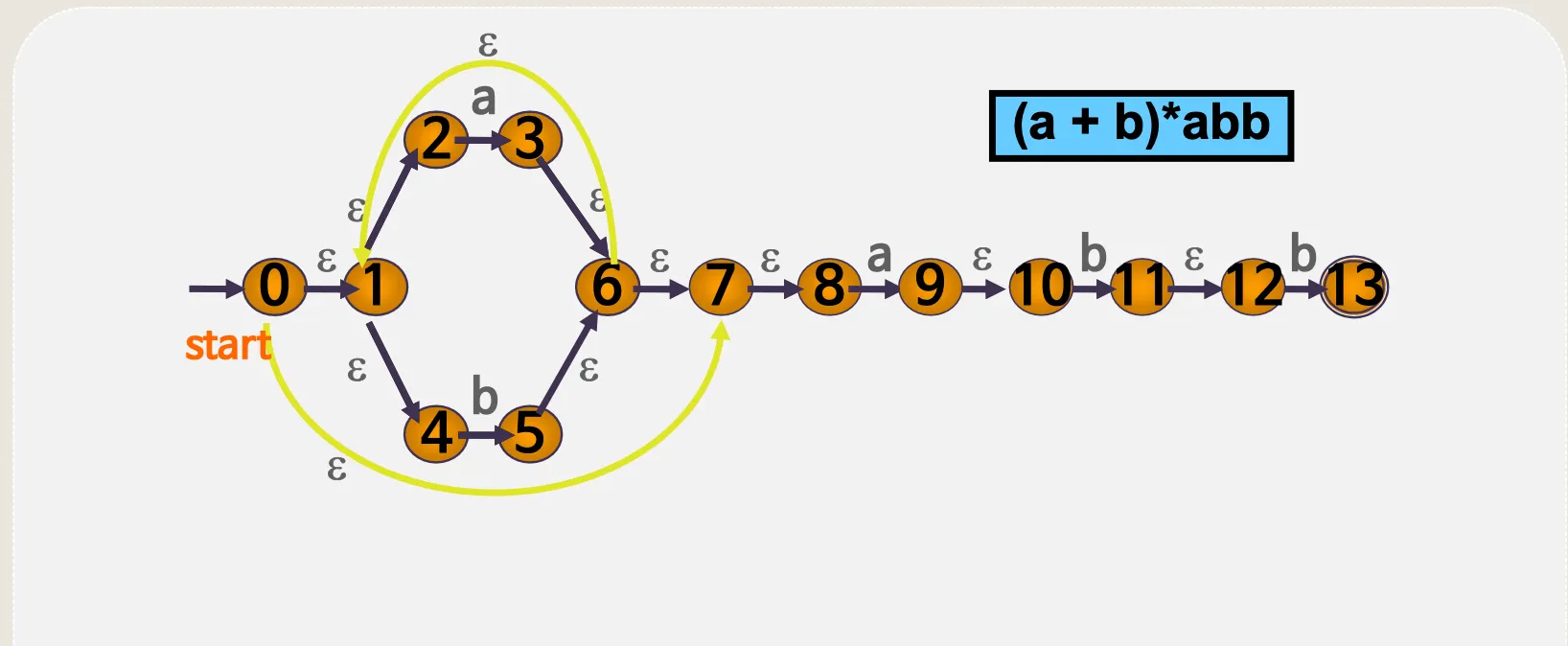
예시
◦
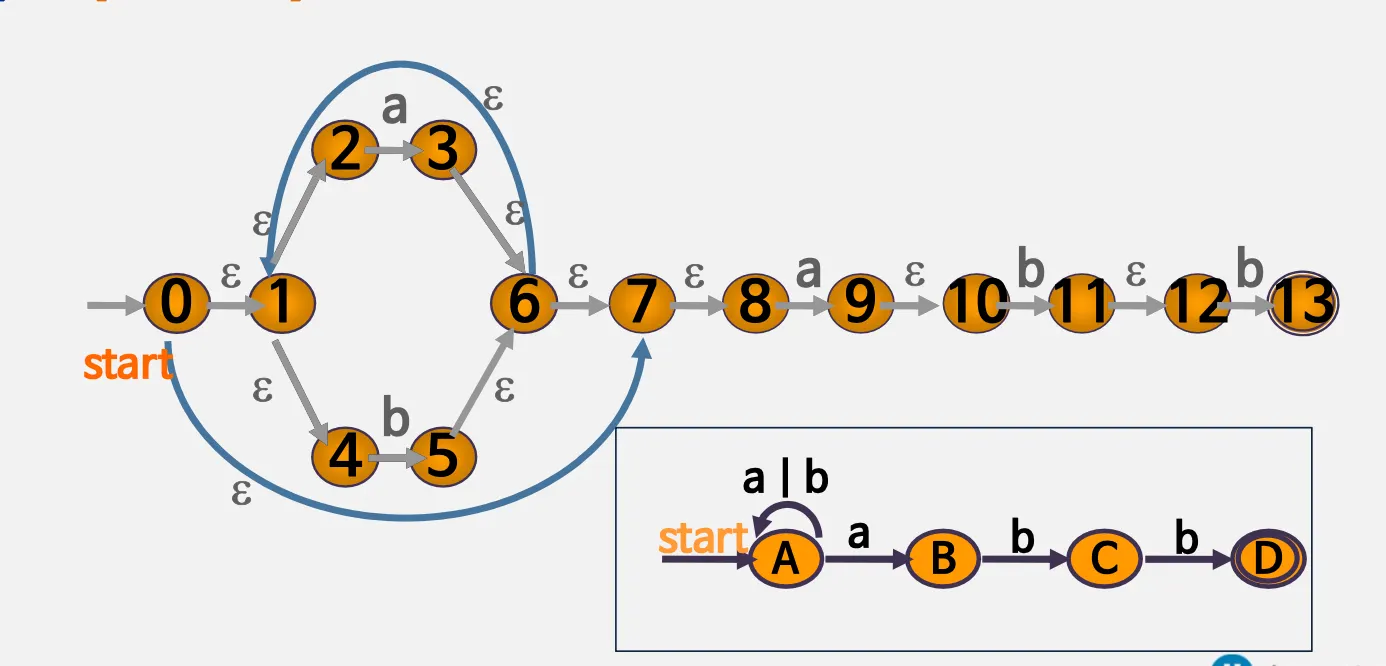
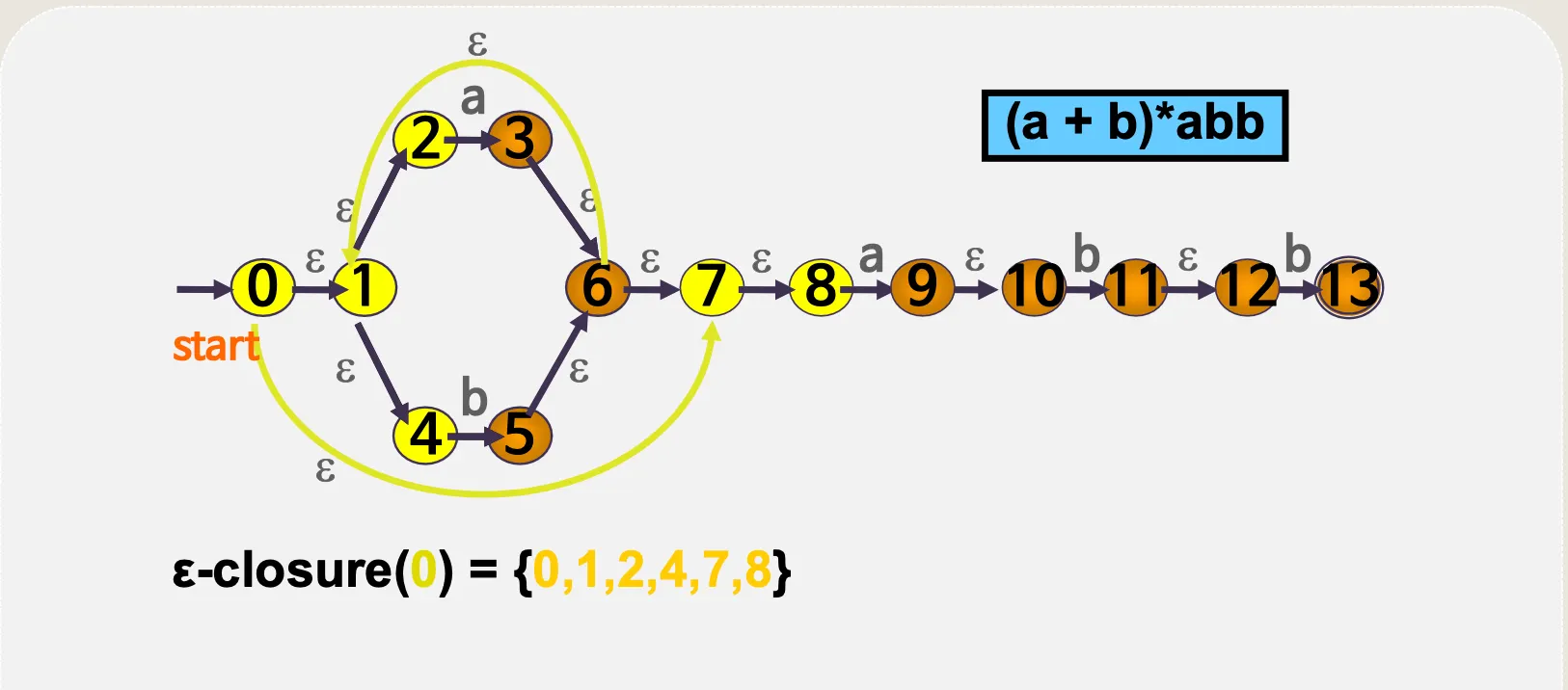
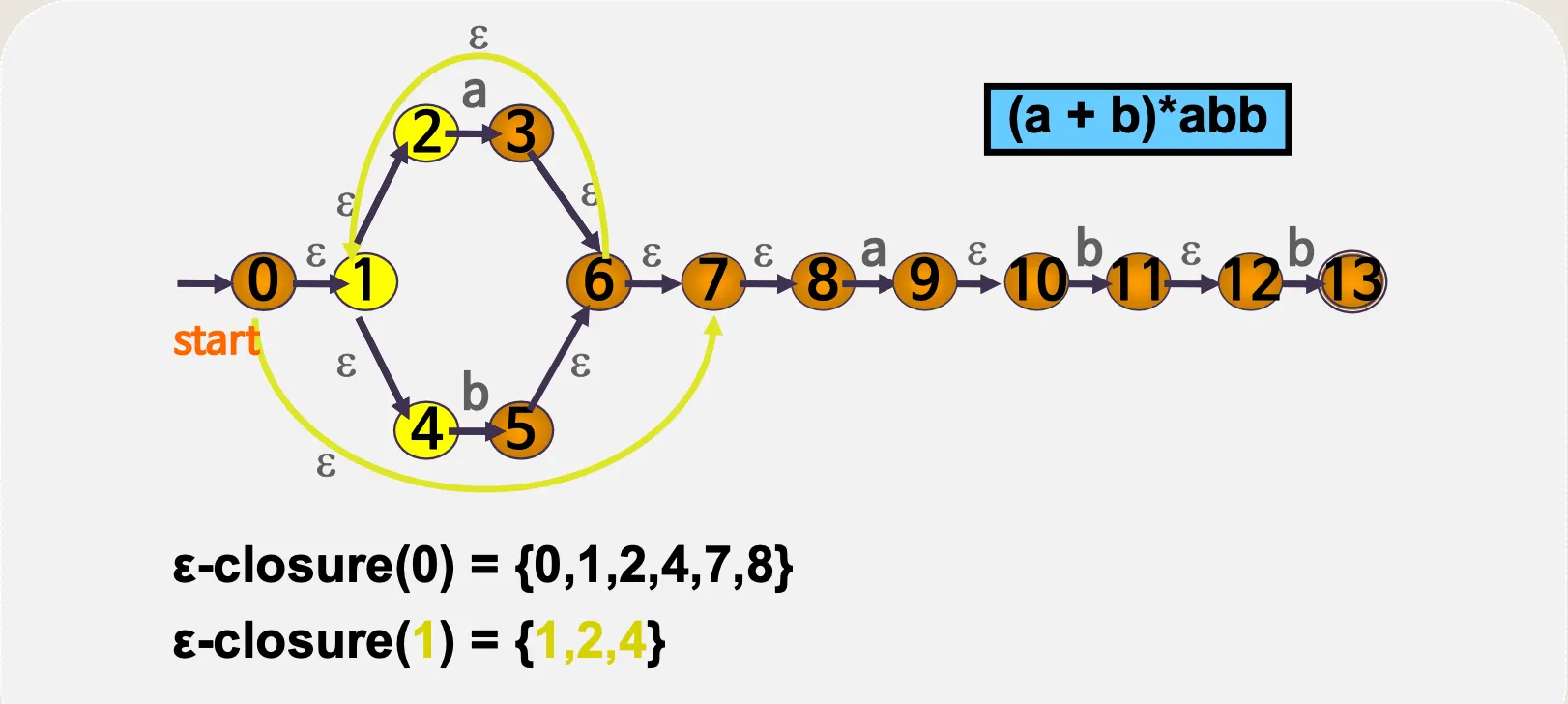
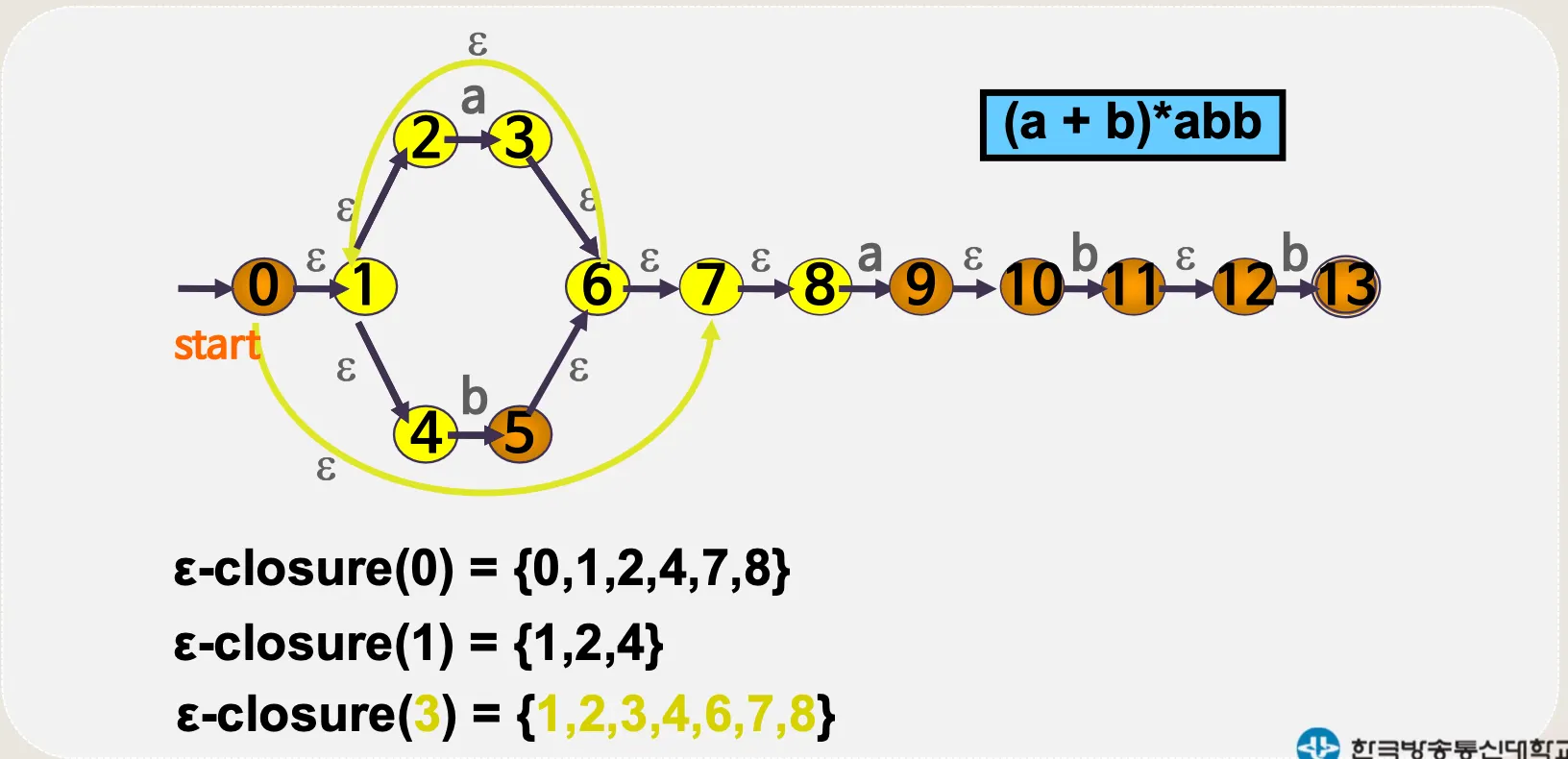
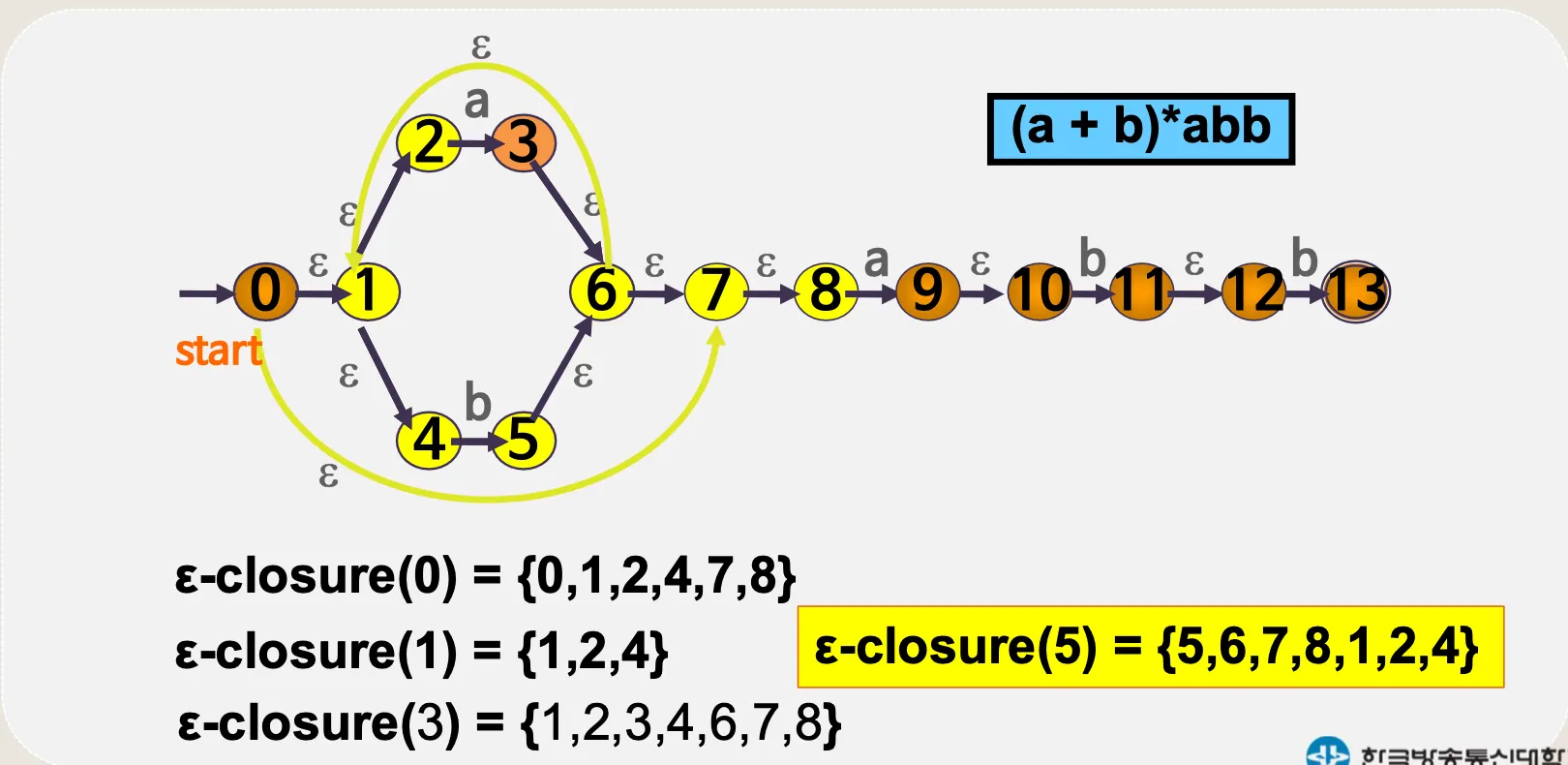
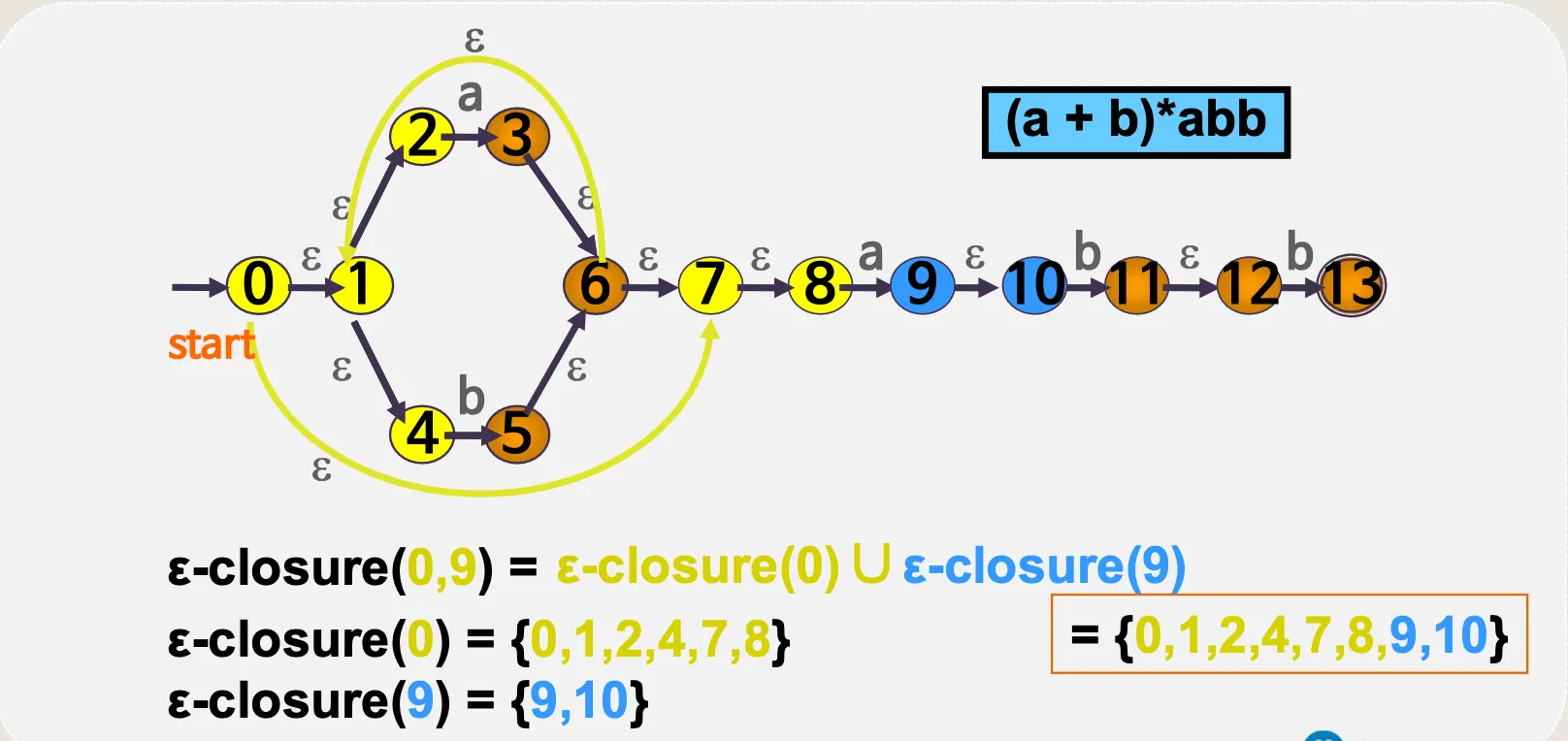
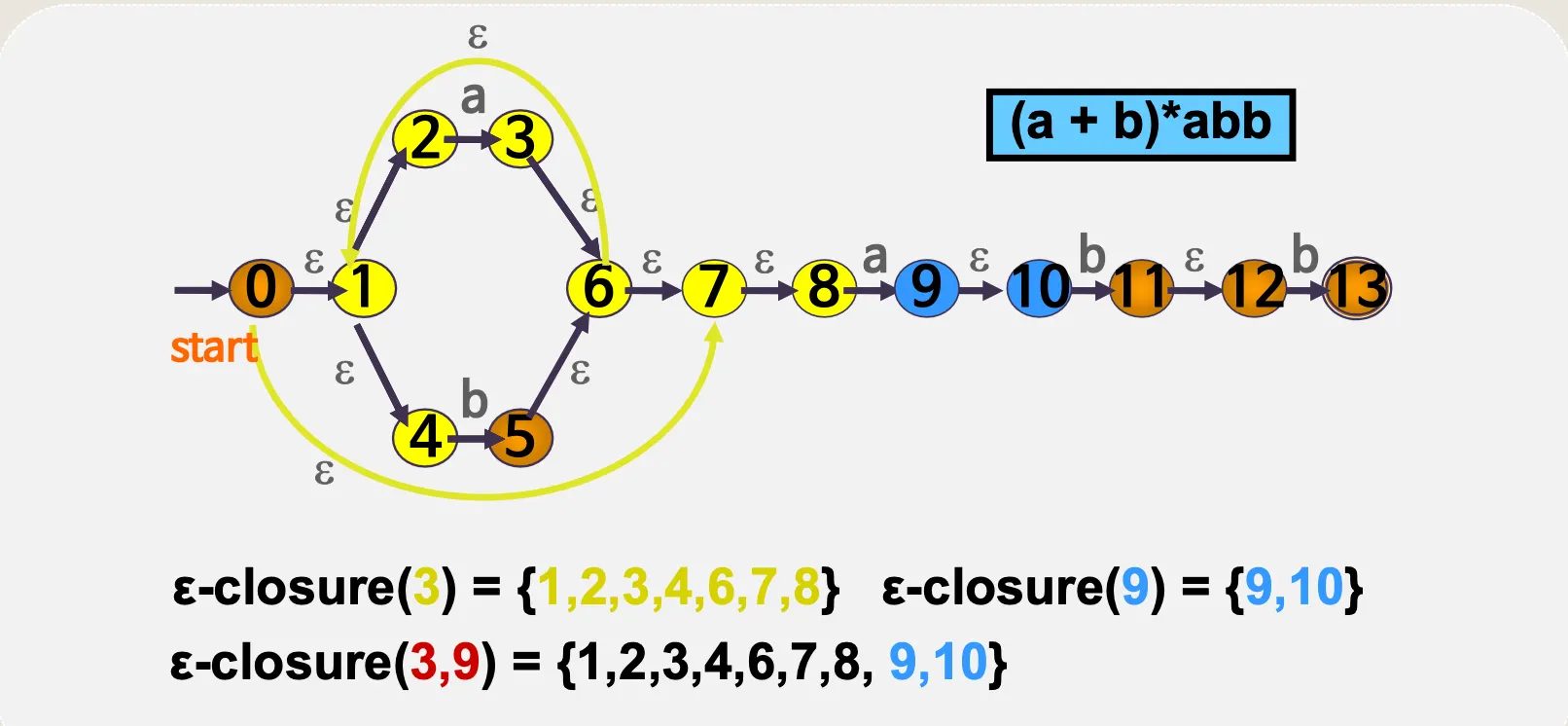
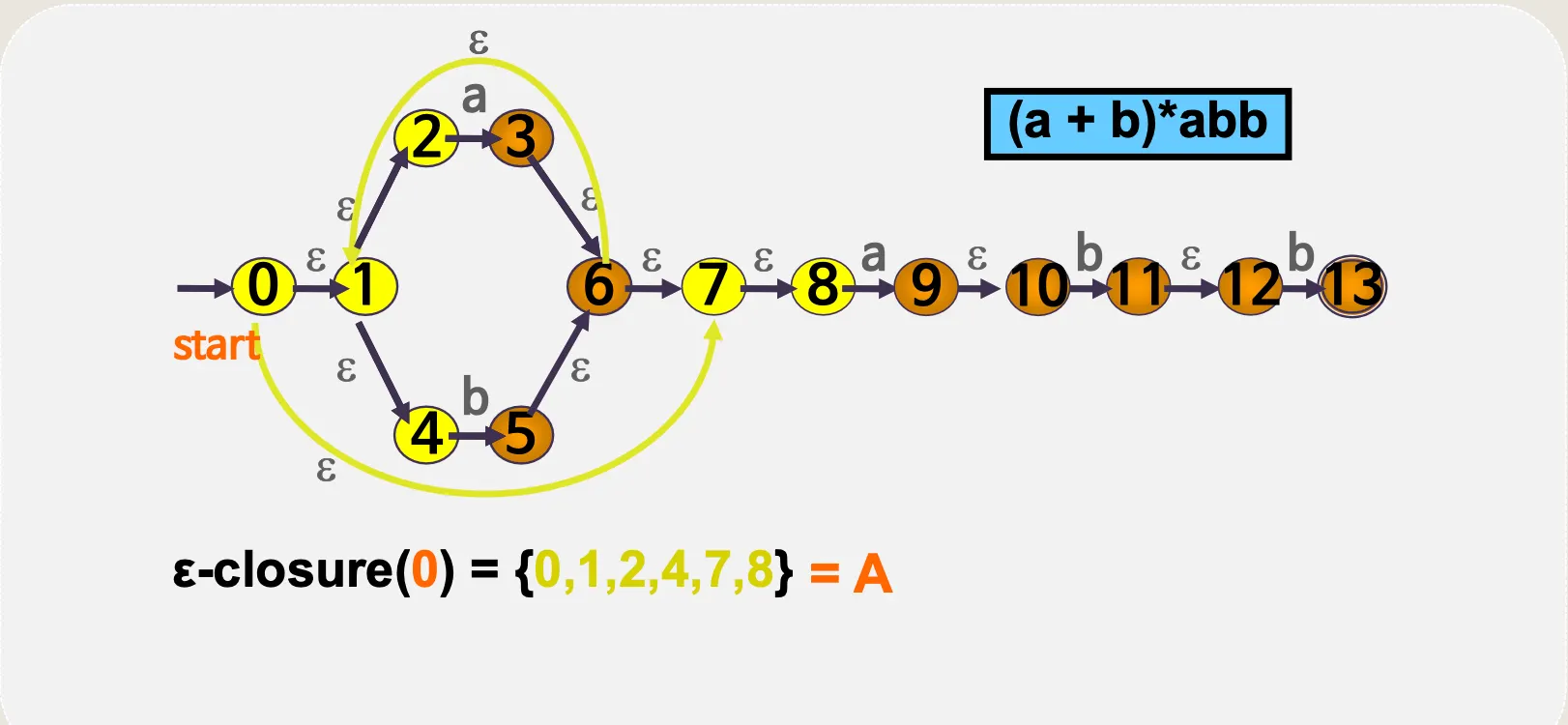
(a + b)*abb
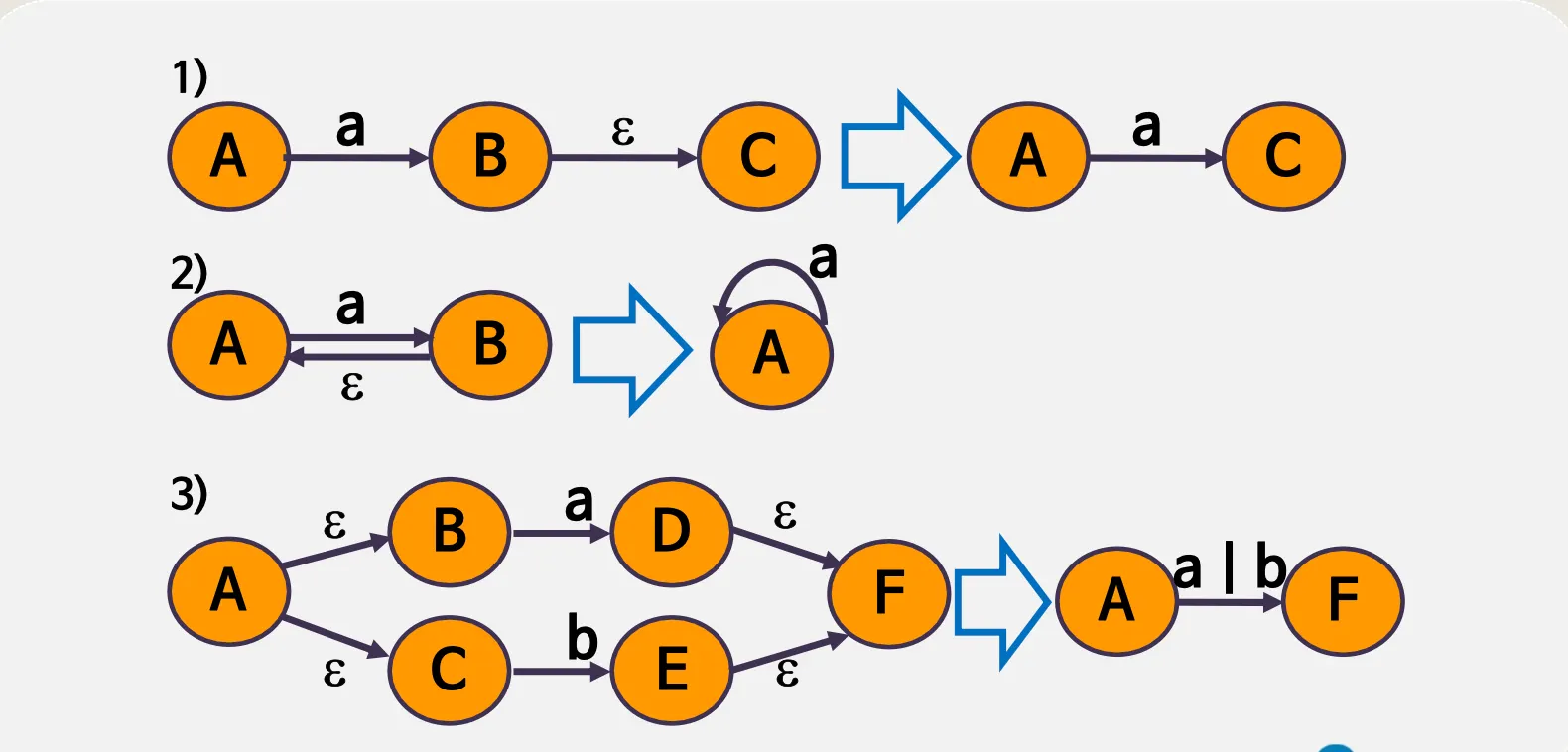
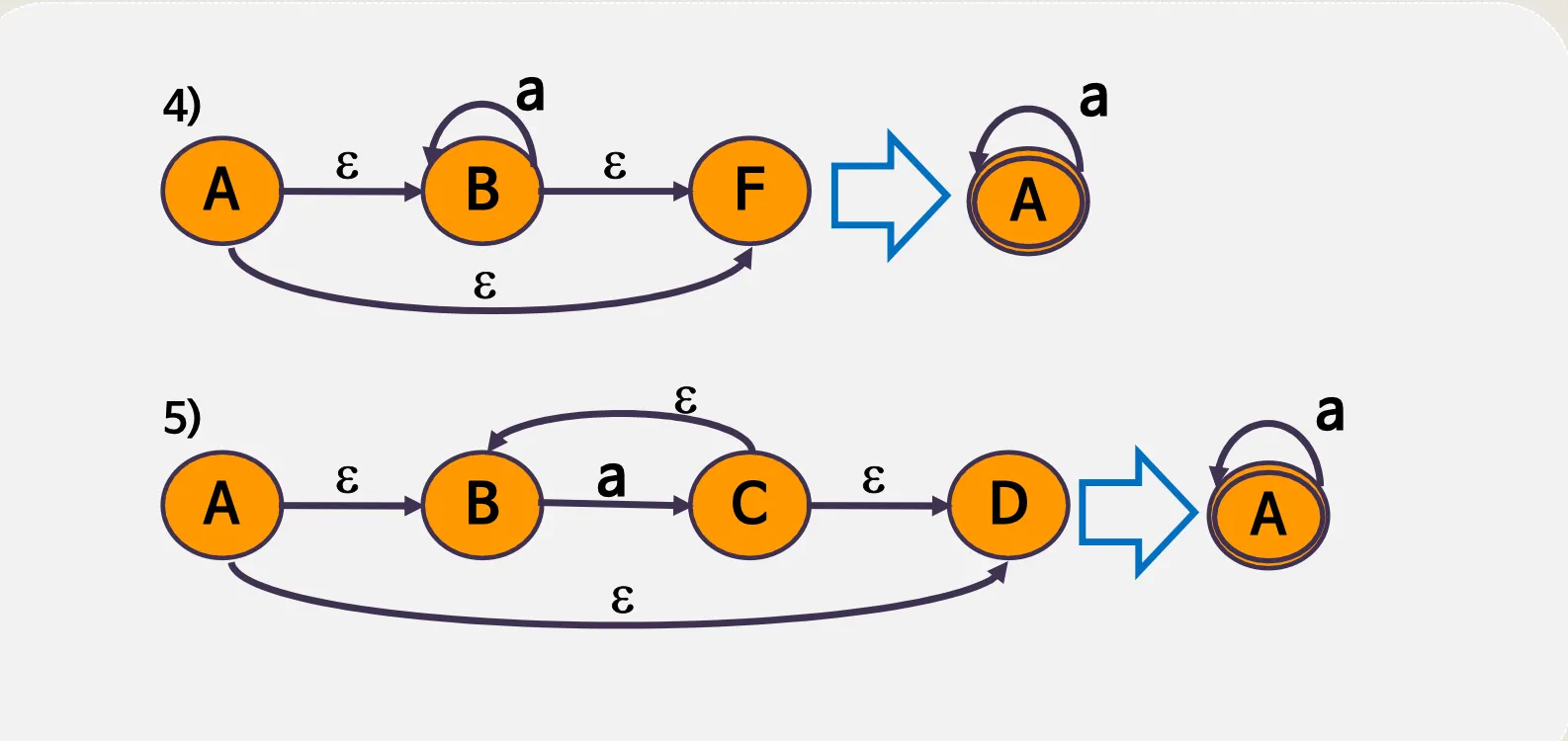
2.2. 유한오토마타의 단순화
•
예시
◦
(a + b)*abb
3. NFA와 DFA의 동치관계
3.1. 유한오토마타(FA) 의 종류
•
결정적 유한오토마타
•
비결졍적 유한오토마타
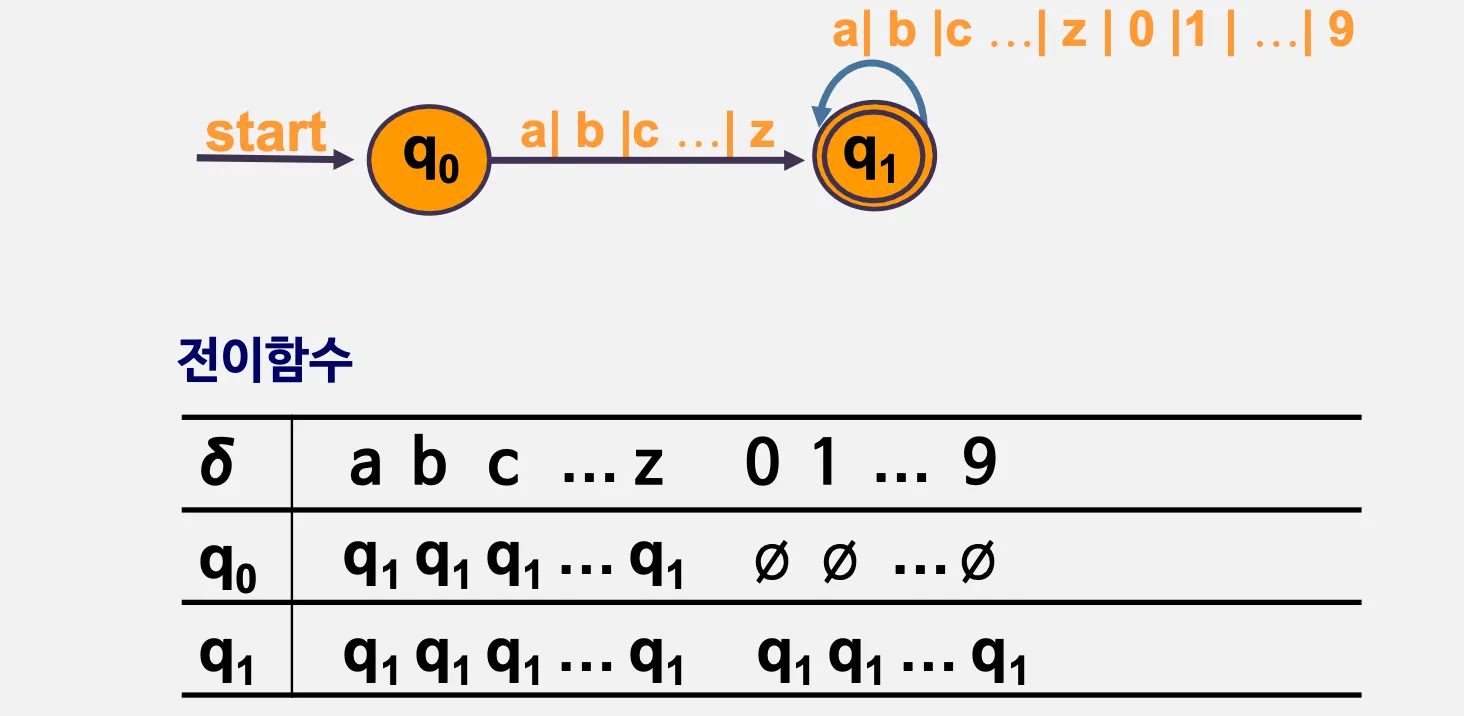
3.2. 결정적 유한오토마타 (DFA)
•
Deterministic Finite Automata
•
하나의 입력기호에 대하여 1개의 상태 전이만 가능
•
전이항수 δ(q,a)가 한 상태만을 갖는 경우
•
한번만에 끝나므로 프로그램이 심플해짐
•
예시)
3.3. 비결정적 유한오토마타 (NFA)
•
Non Deterministic Finite Automata
•
하나의 입력기호에 대하여 2개 이상의 상태 전이, ε–전이가 있음
•
어떤 상태에서 주어진 하나의 입력기호를 보고, 갈 수 있는 다음 상태가 하나 이상 존재할 경우
•
구현이 복잡하고 성능 저하
•
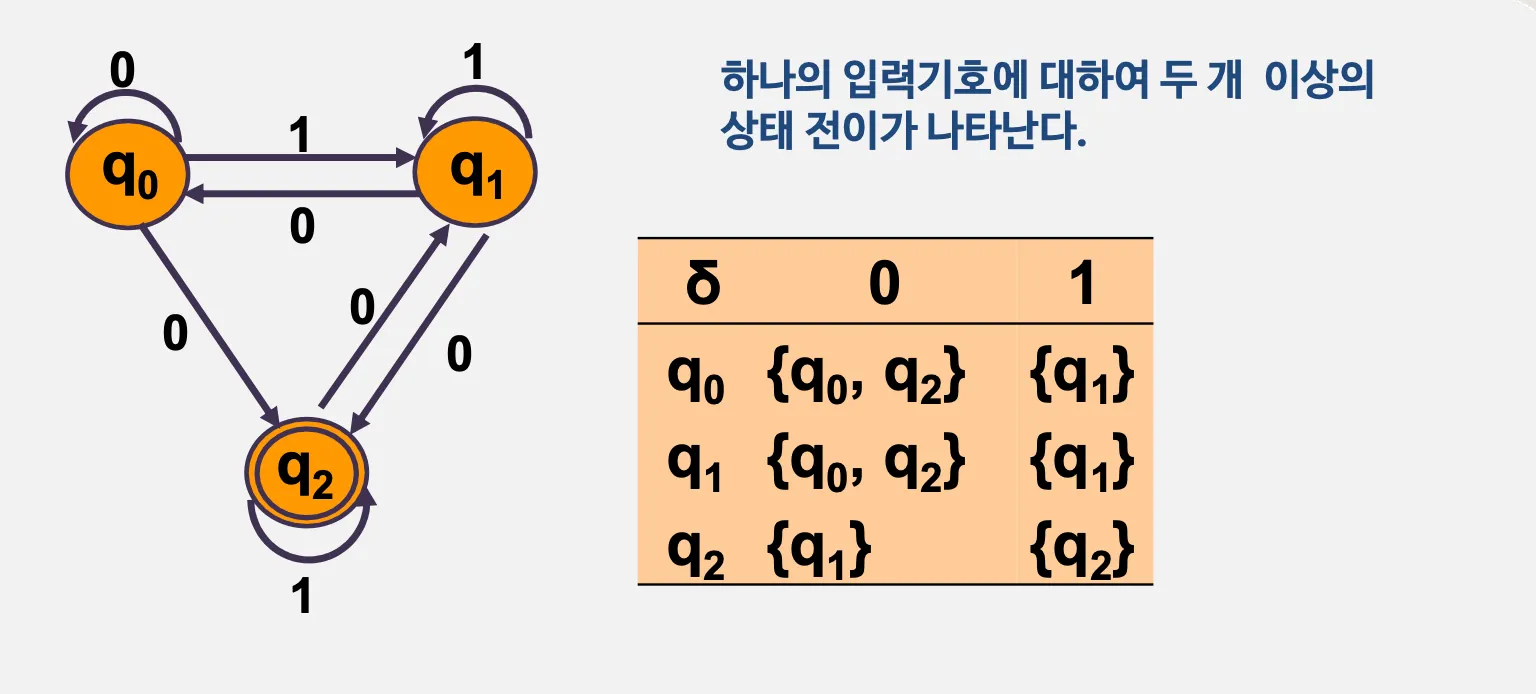
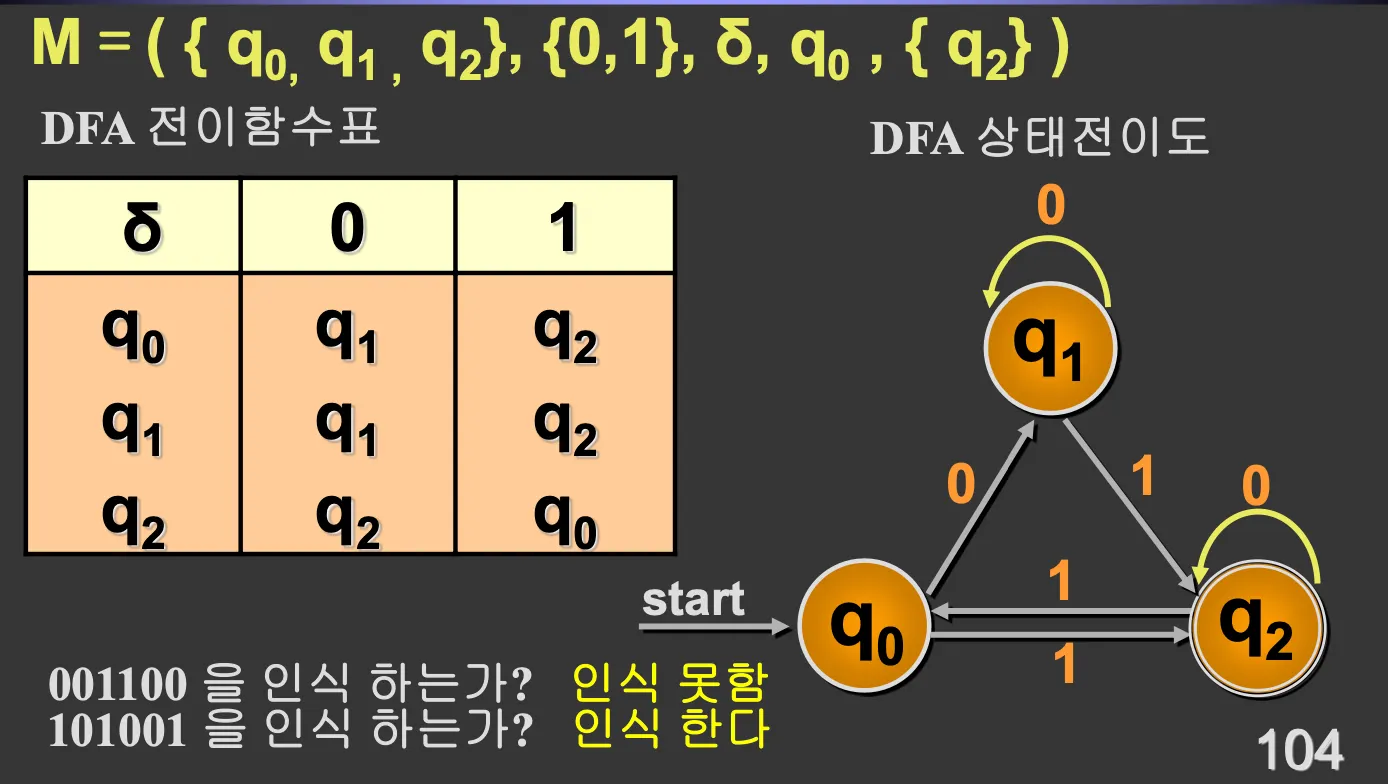
예시)
◦
Q: 상태 = {q0, q1, q2)
◦
Σ: 입력기호 = {0, 1}
◦
q0: 시작상태 = q0
◦
F: 종료상태 = {q2}
•
종류
◦
ε–전이
▪
ε(앱실론)을 보고 한 상태에서 다음 상태로 이동하는 것을 의미
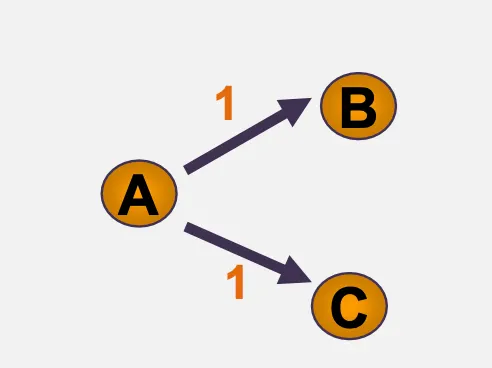
◦
2개 이상의 상태 전이
▪
하나의 입력기호에 대하여 두 개 이상의상태 전이가 나타난다.
•
DFA와 NFA의 동치관계
◦
DFA와 NFA는 서로가 동등하다.
◦
DFA ⊂ NFA 이므로 NFA ⊂ DFA 임을 증명 해주면 된다.
4. NFA 전이
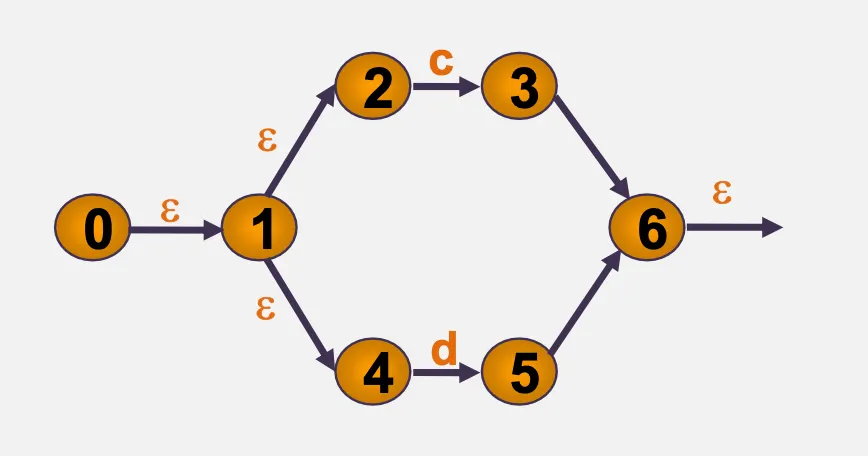
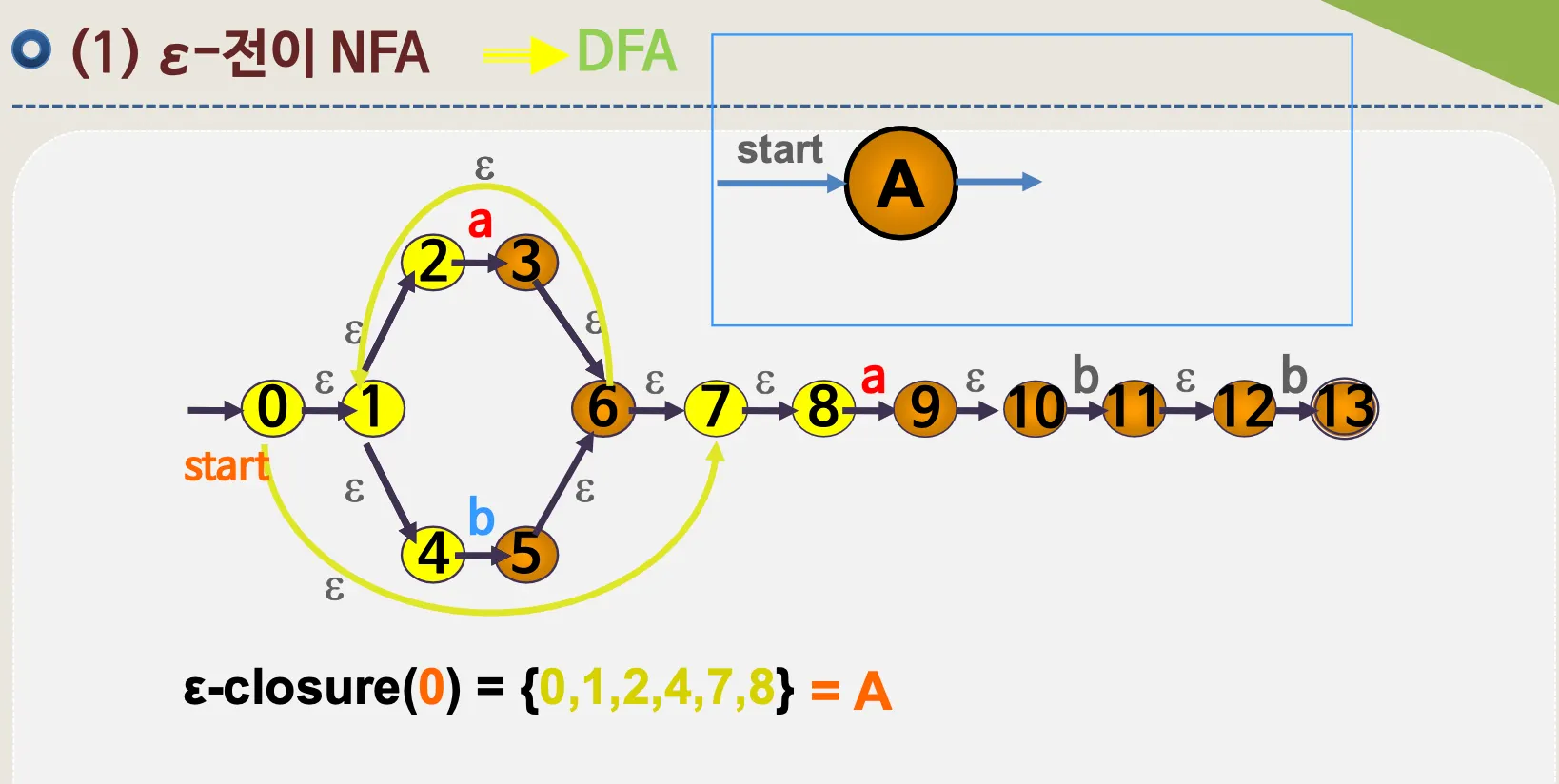
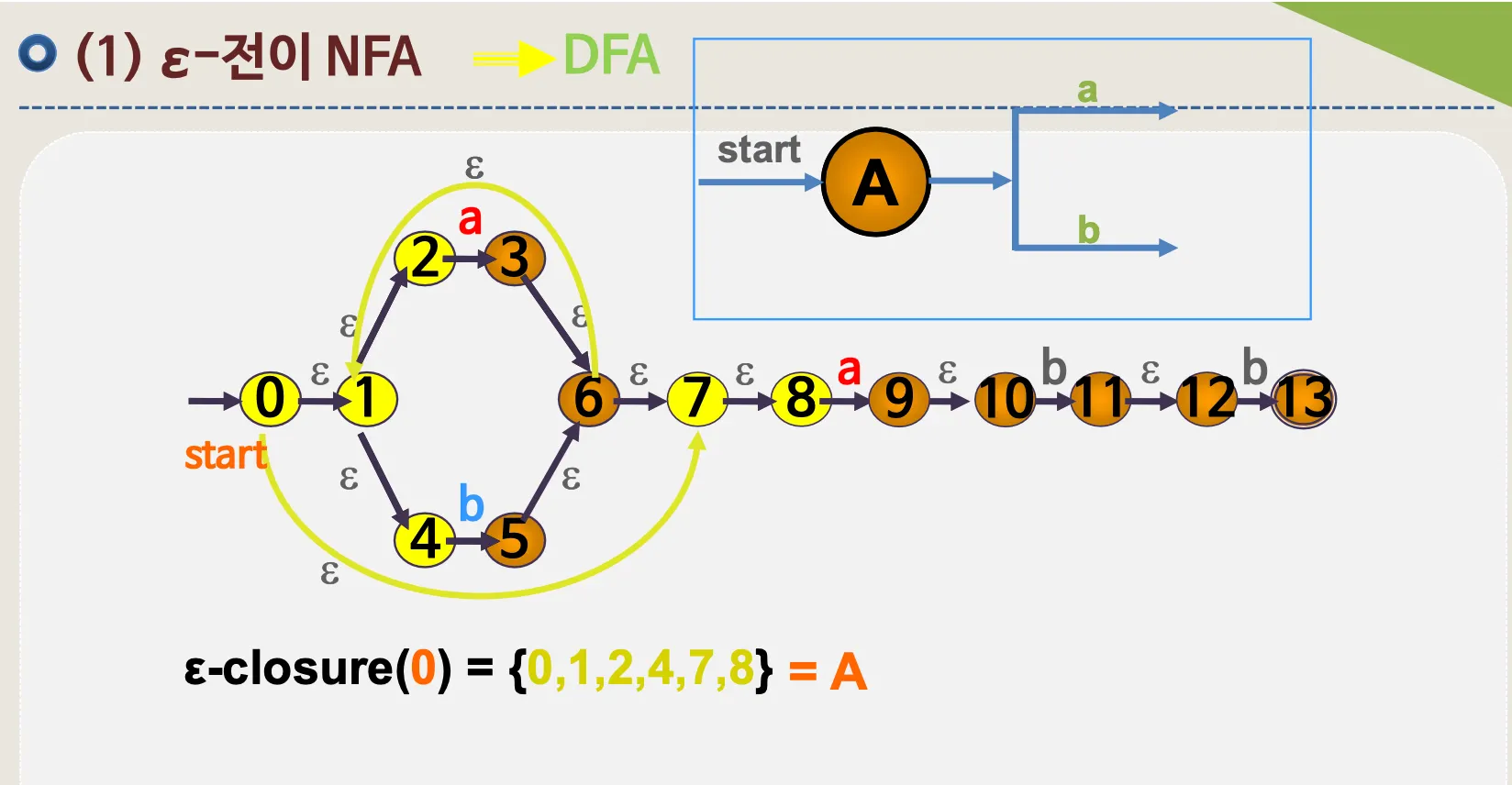
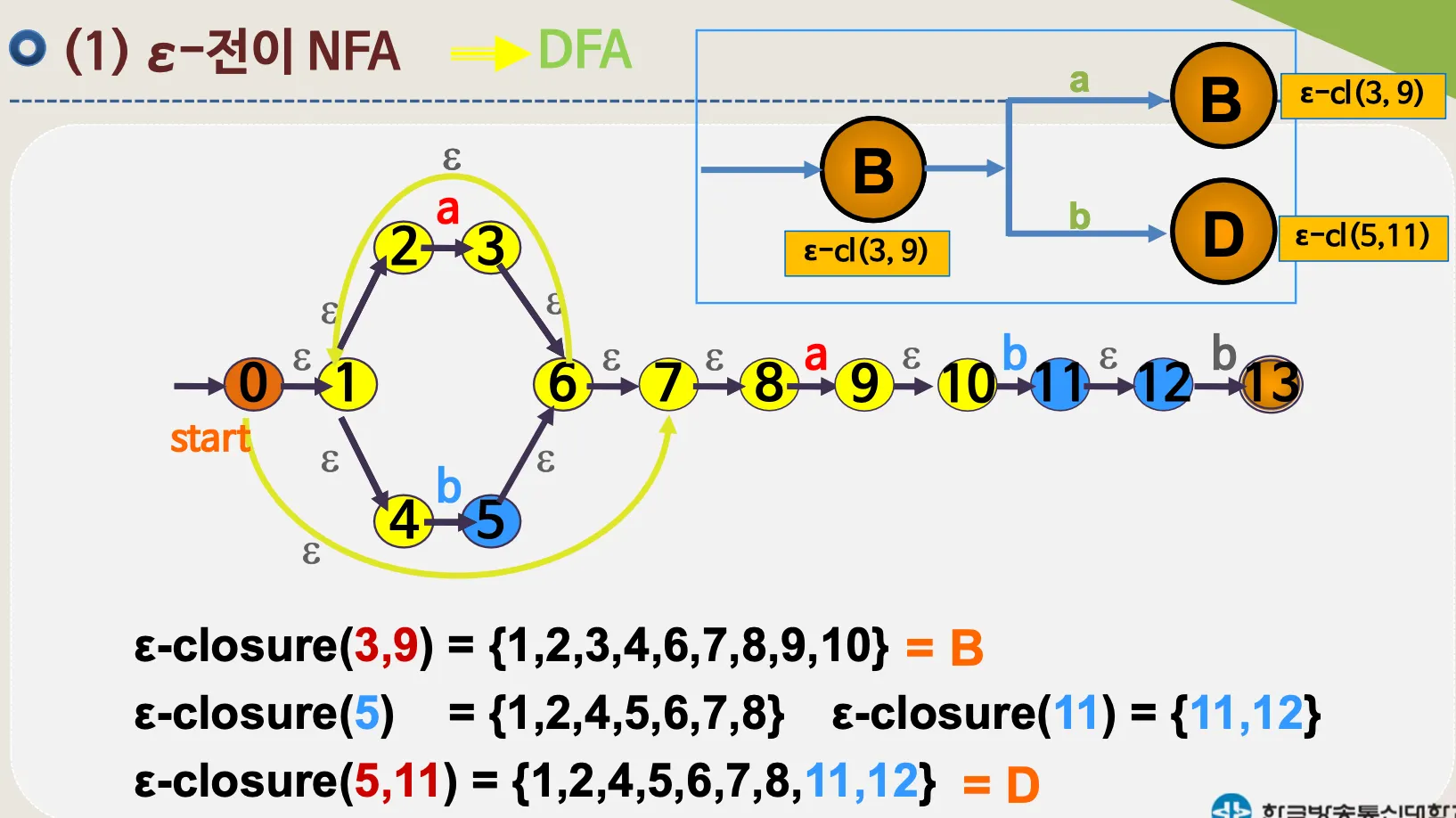
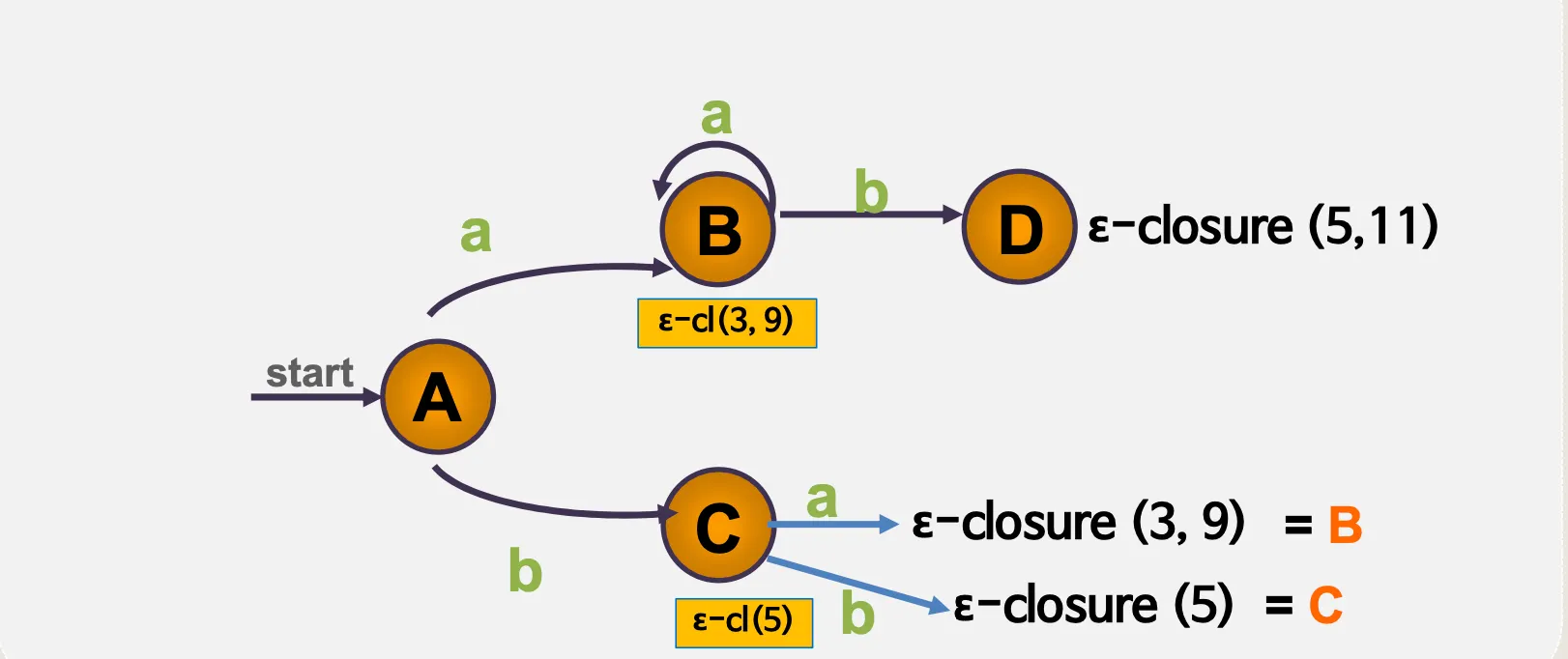
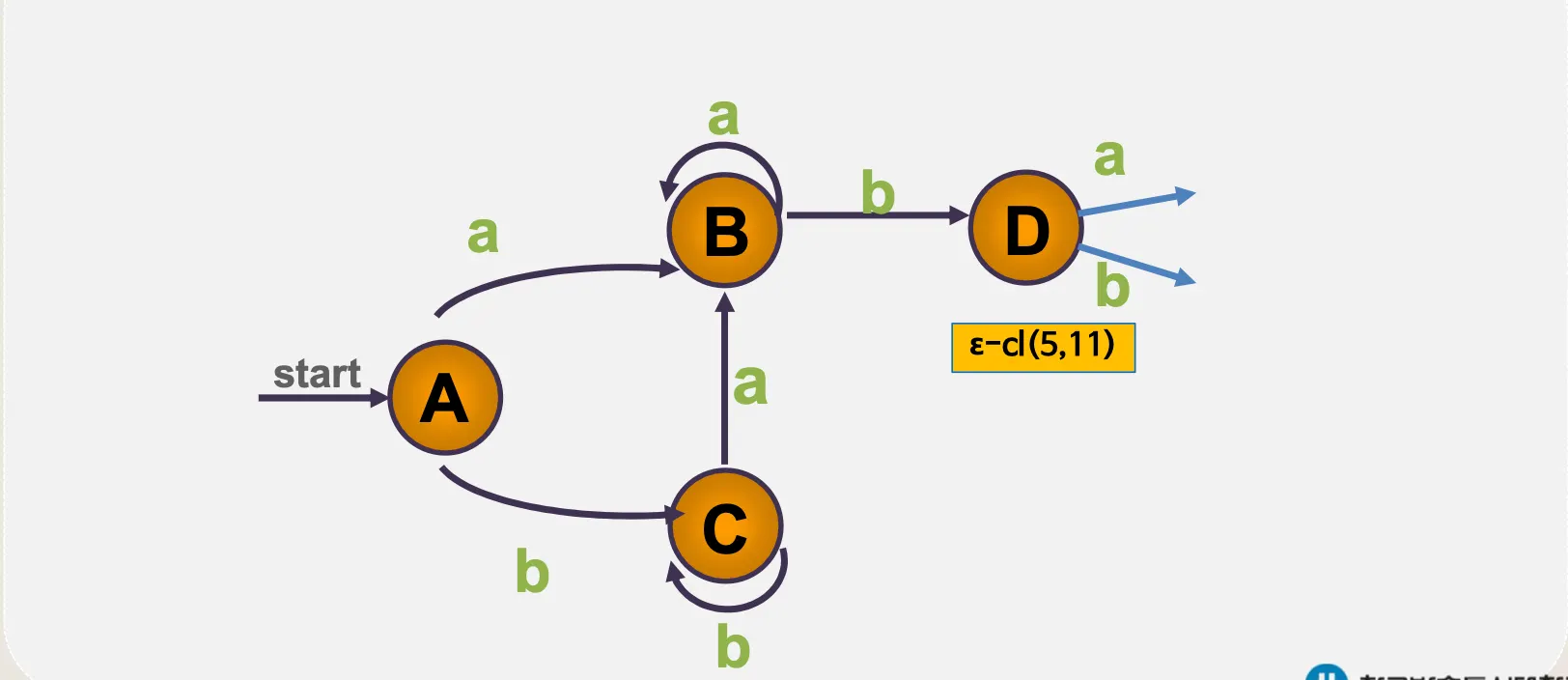
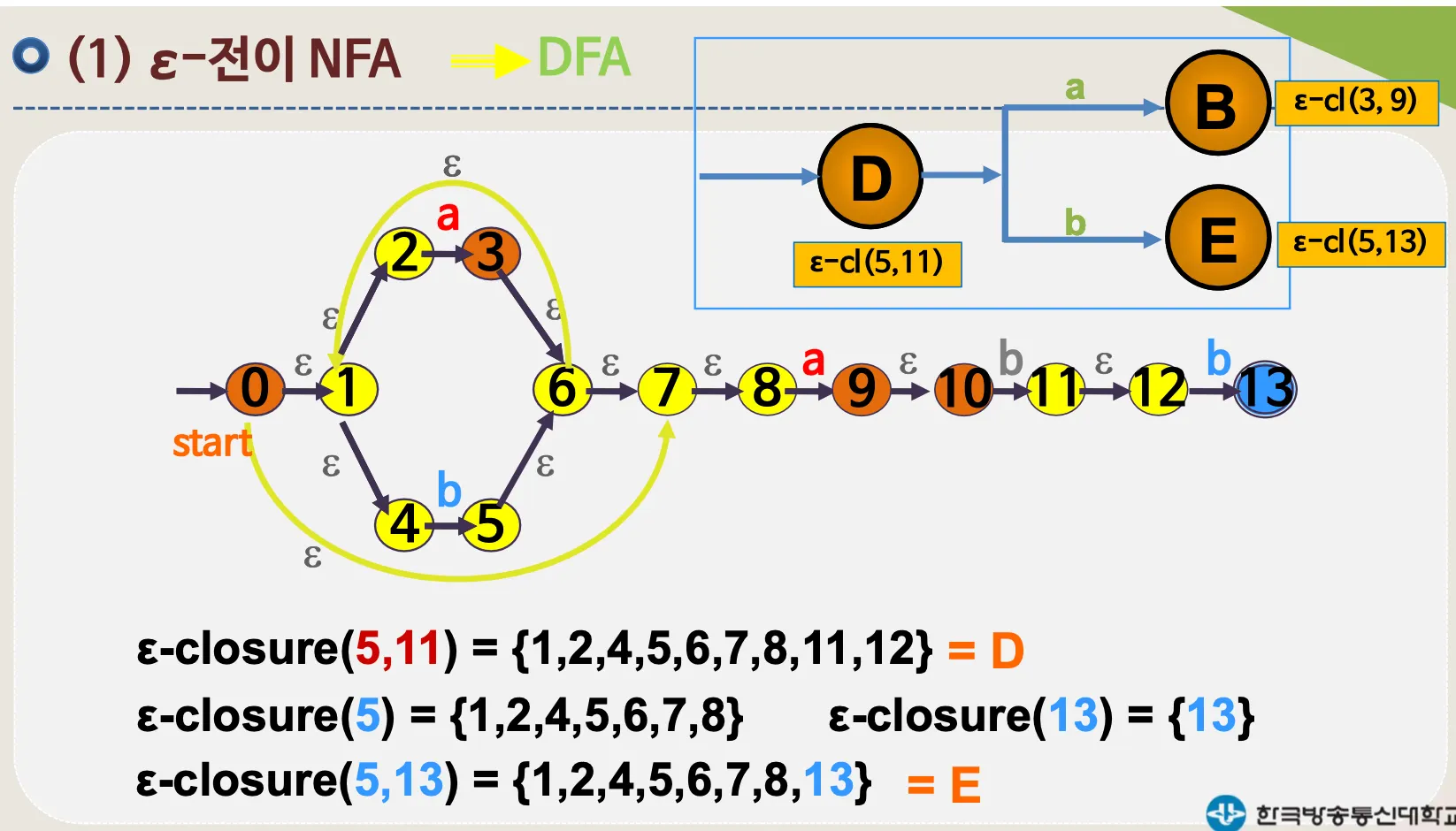
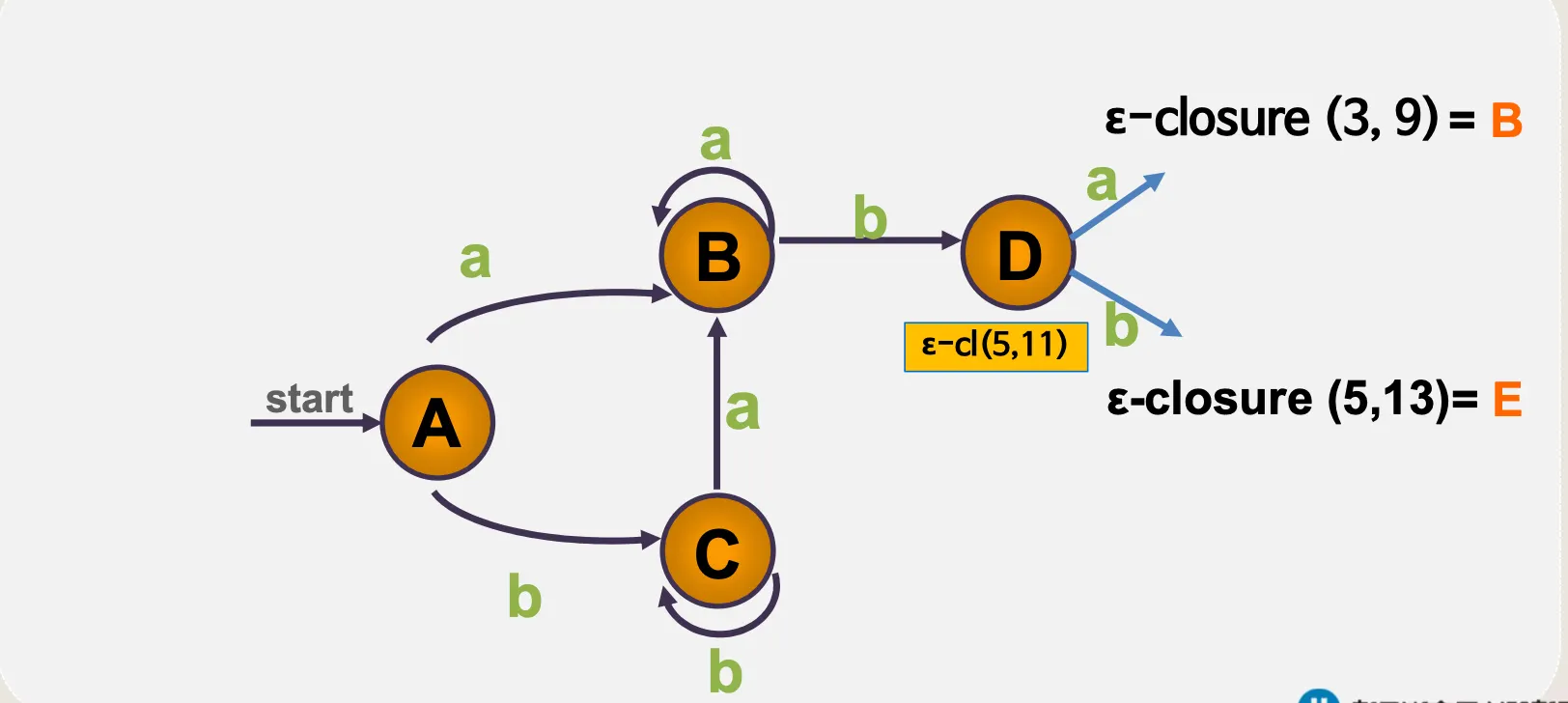
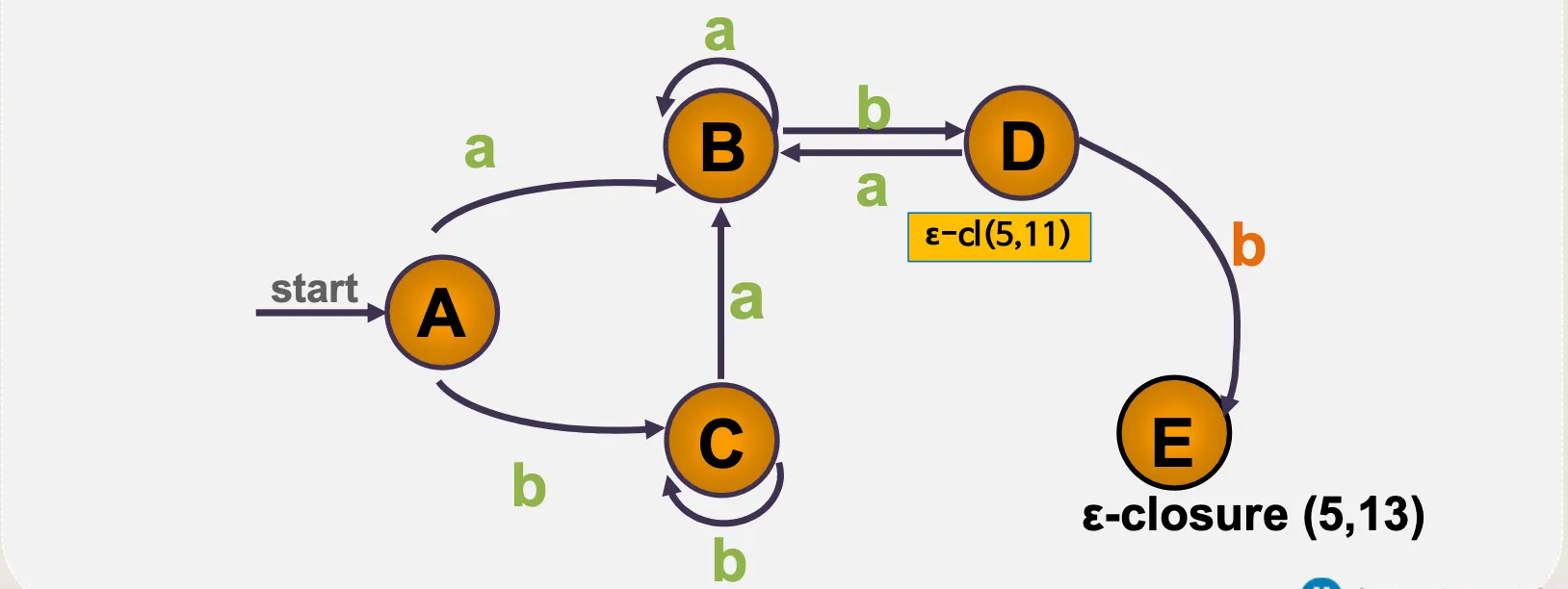
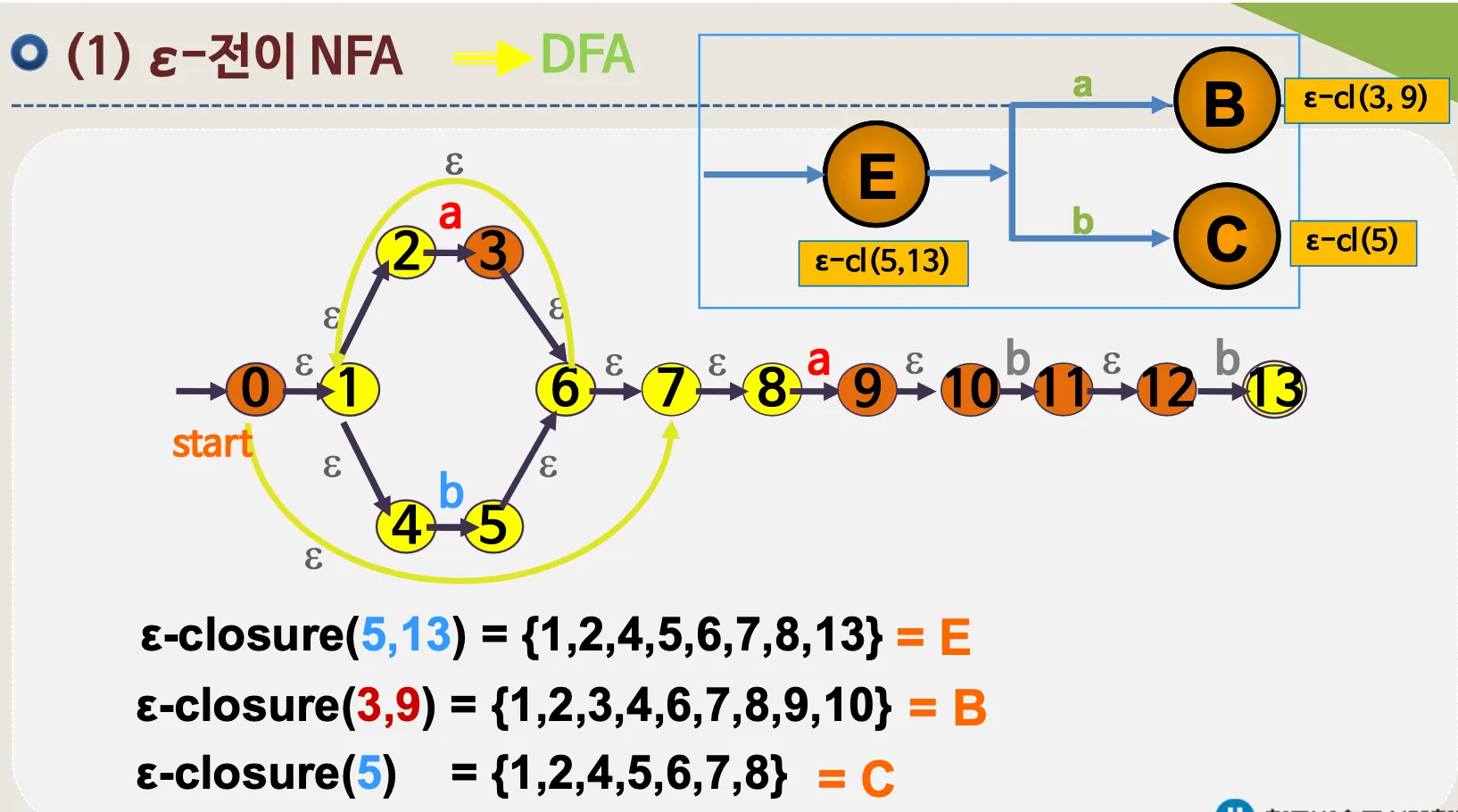
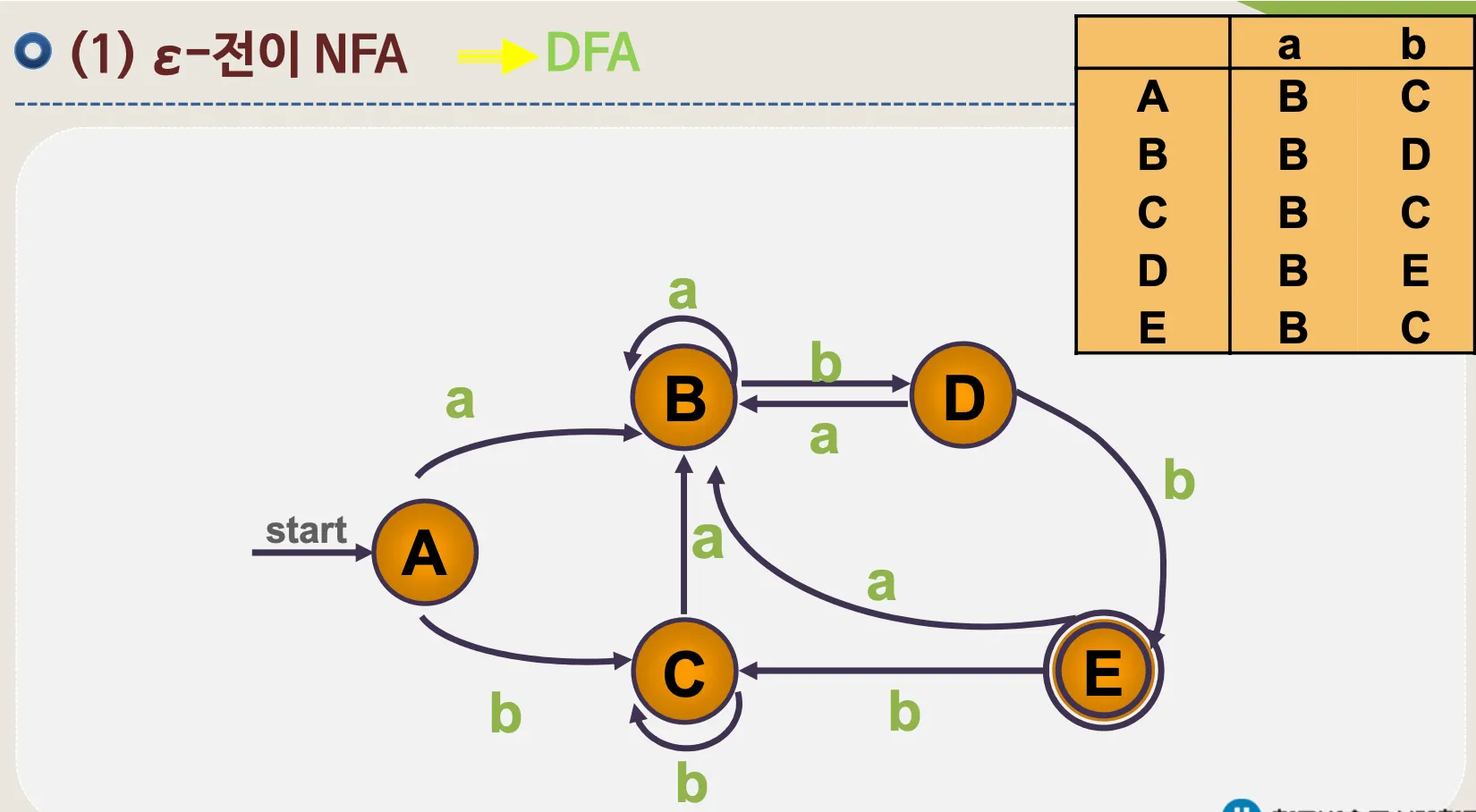
4.1. ε–전이 NFA
•
예시
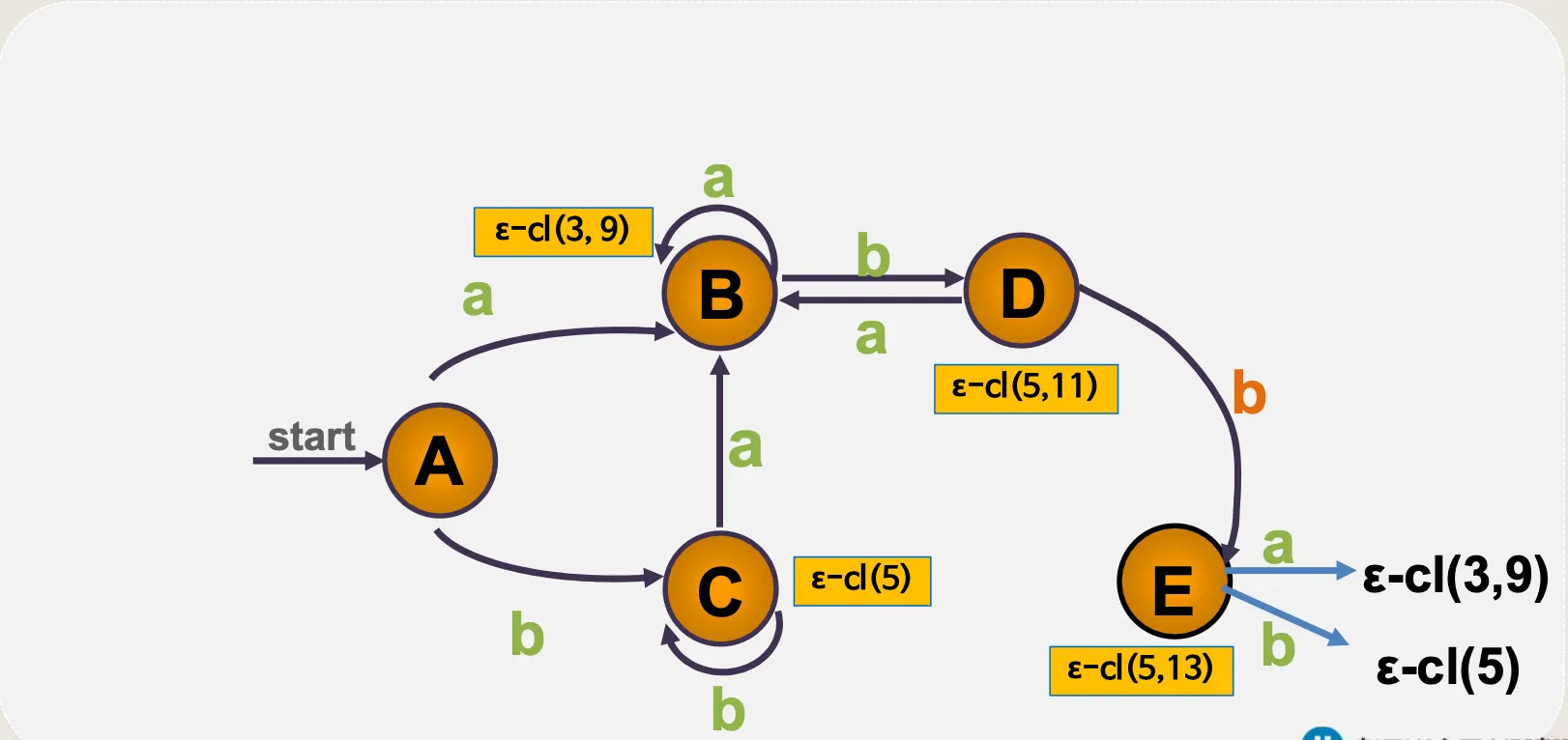
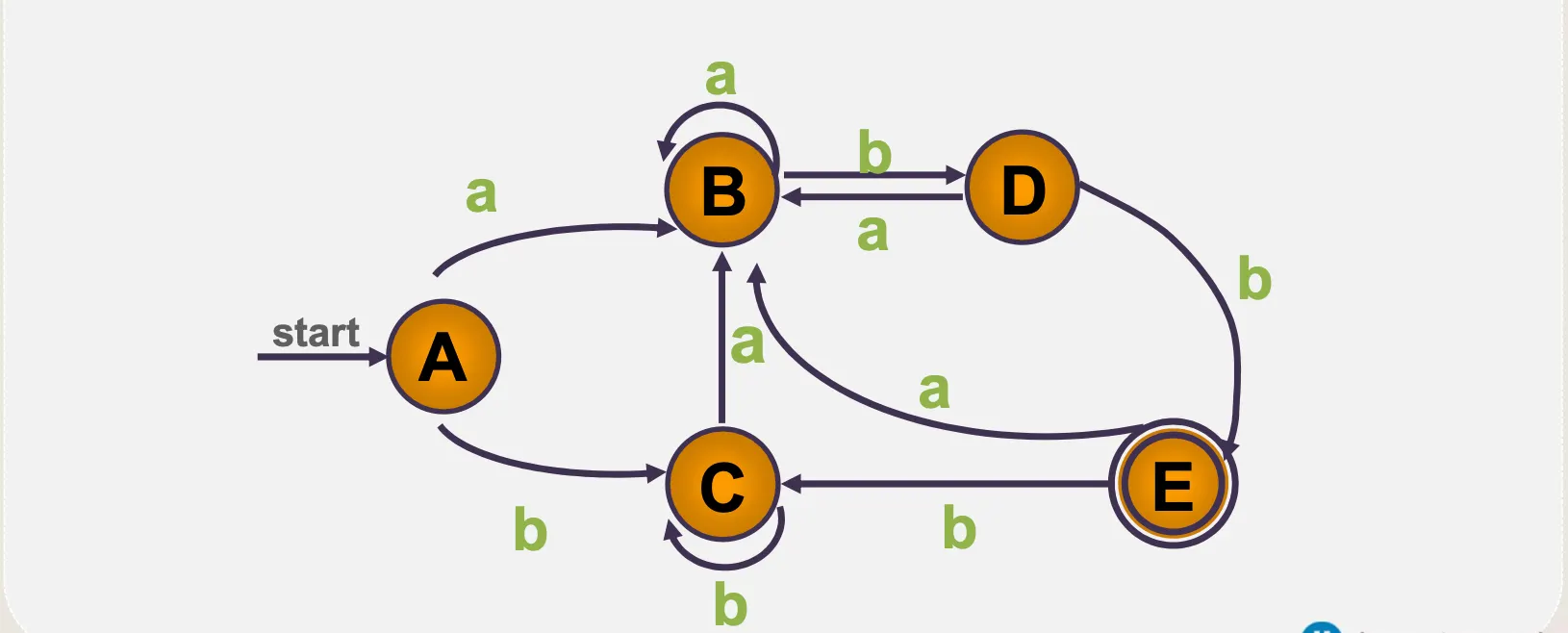
•
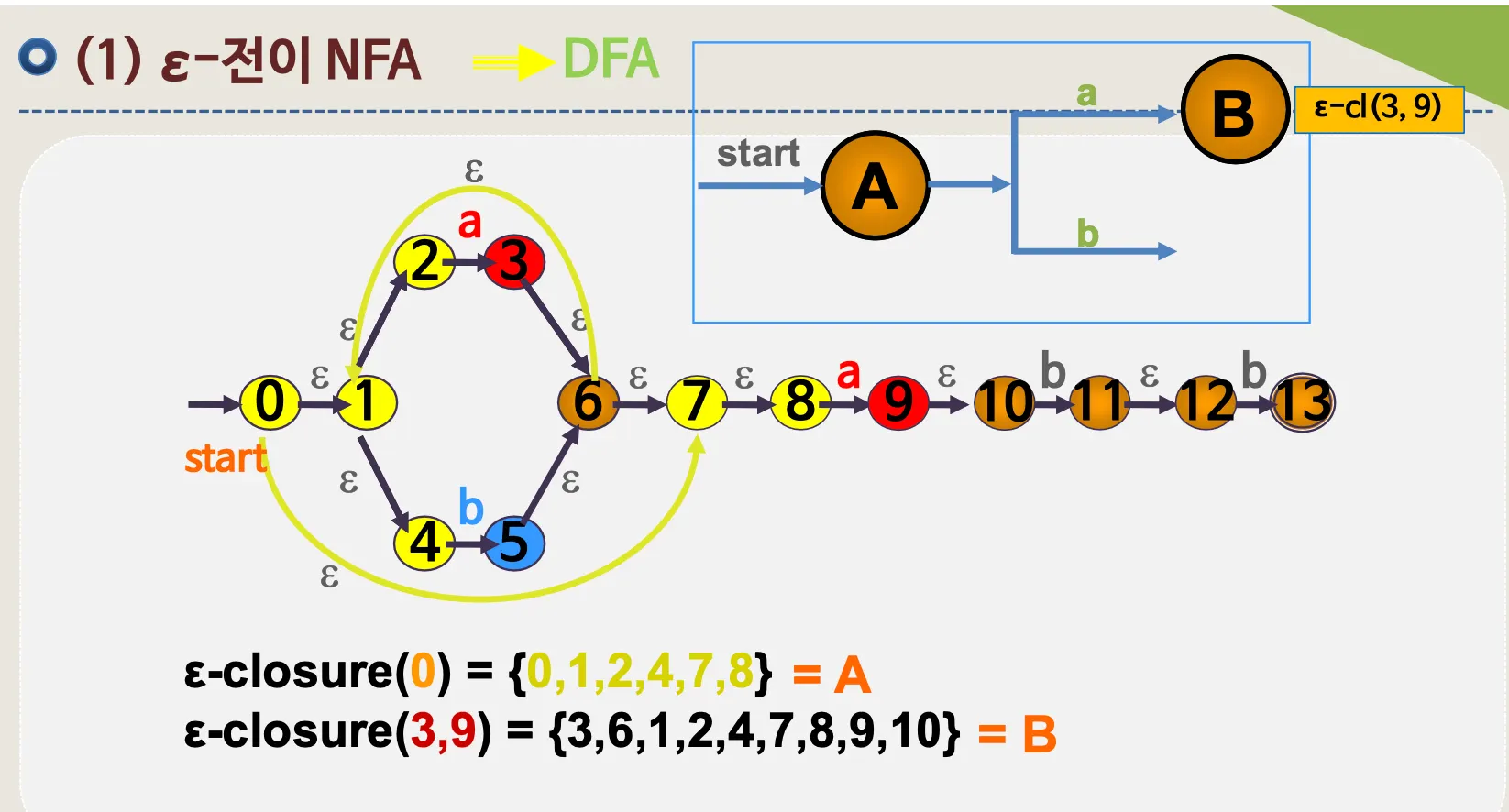
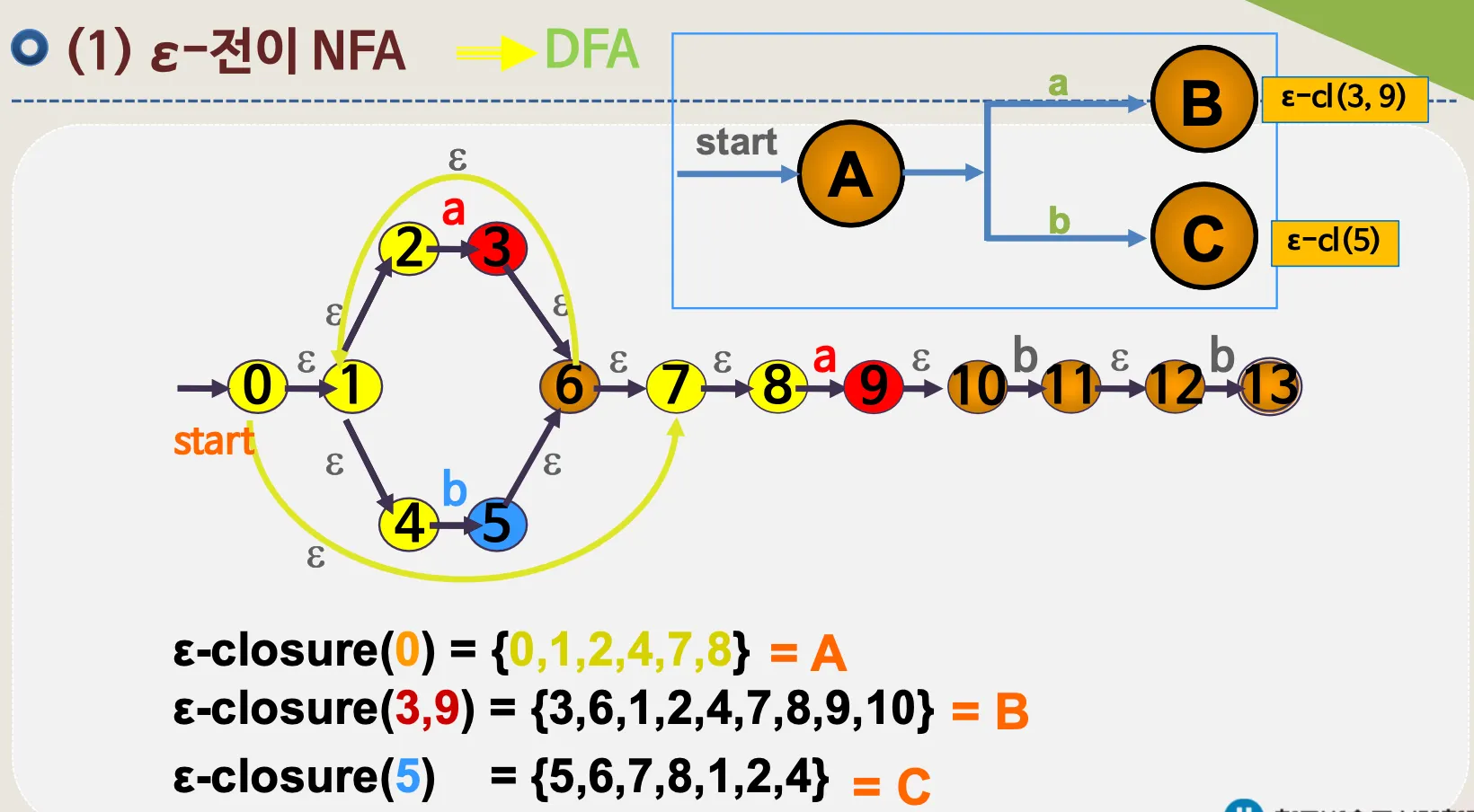
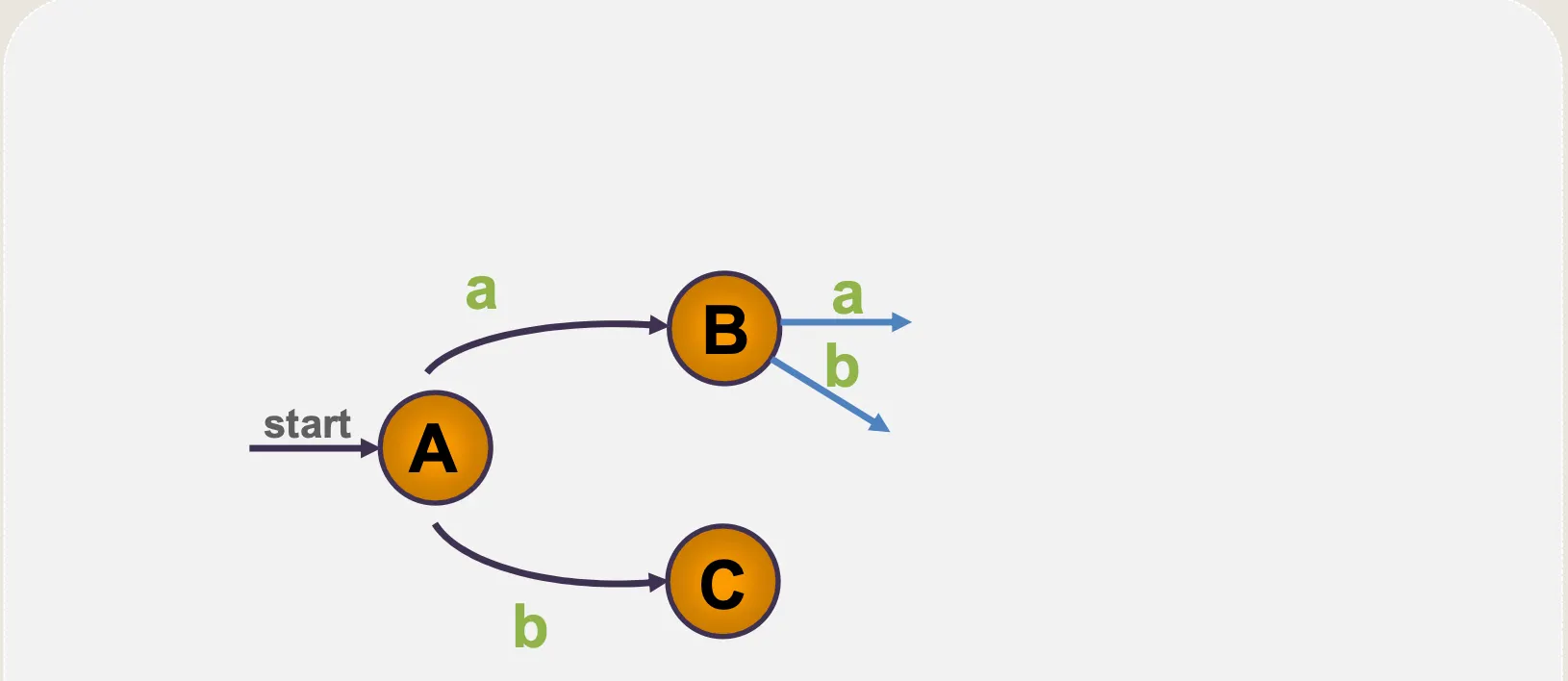
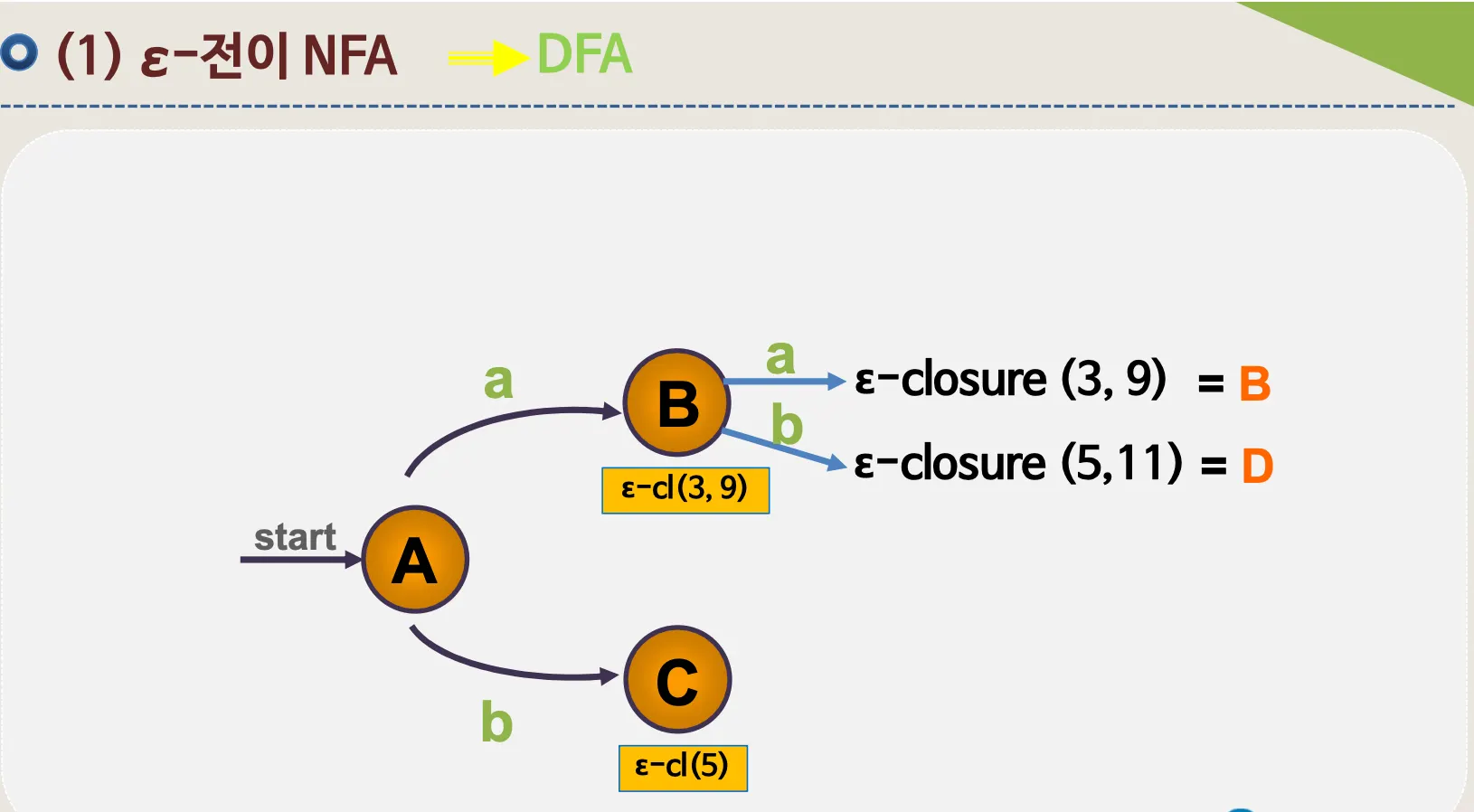
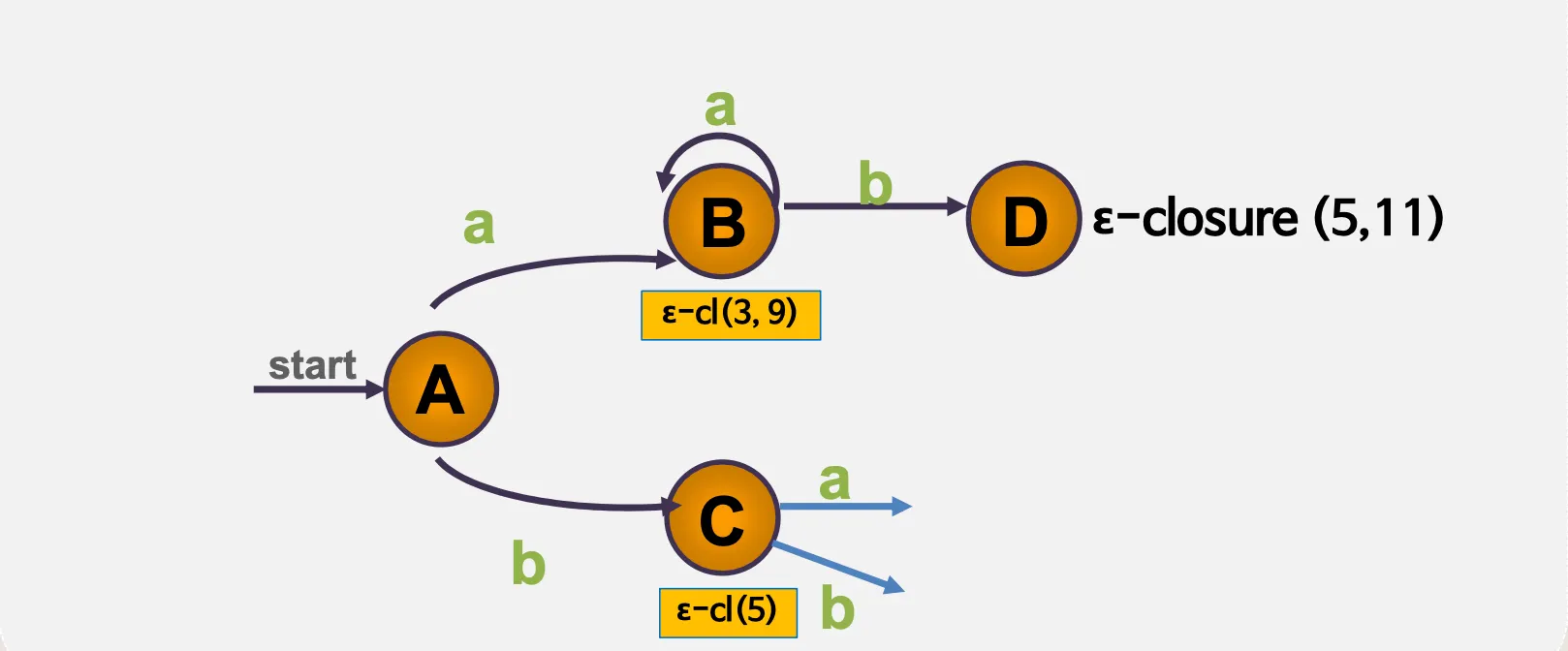
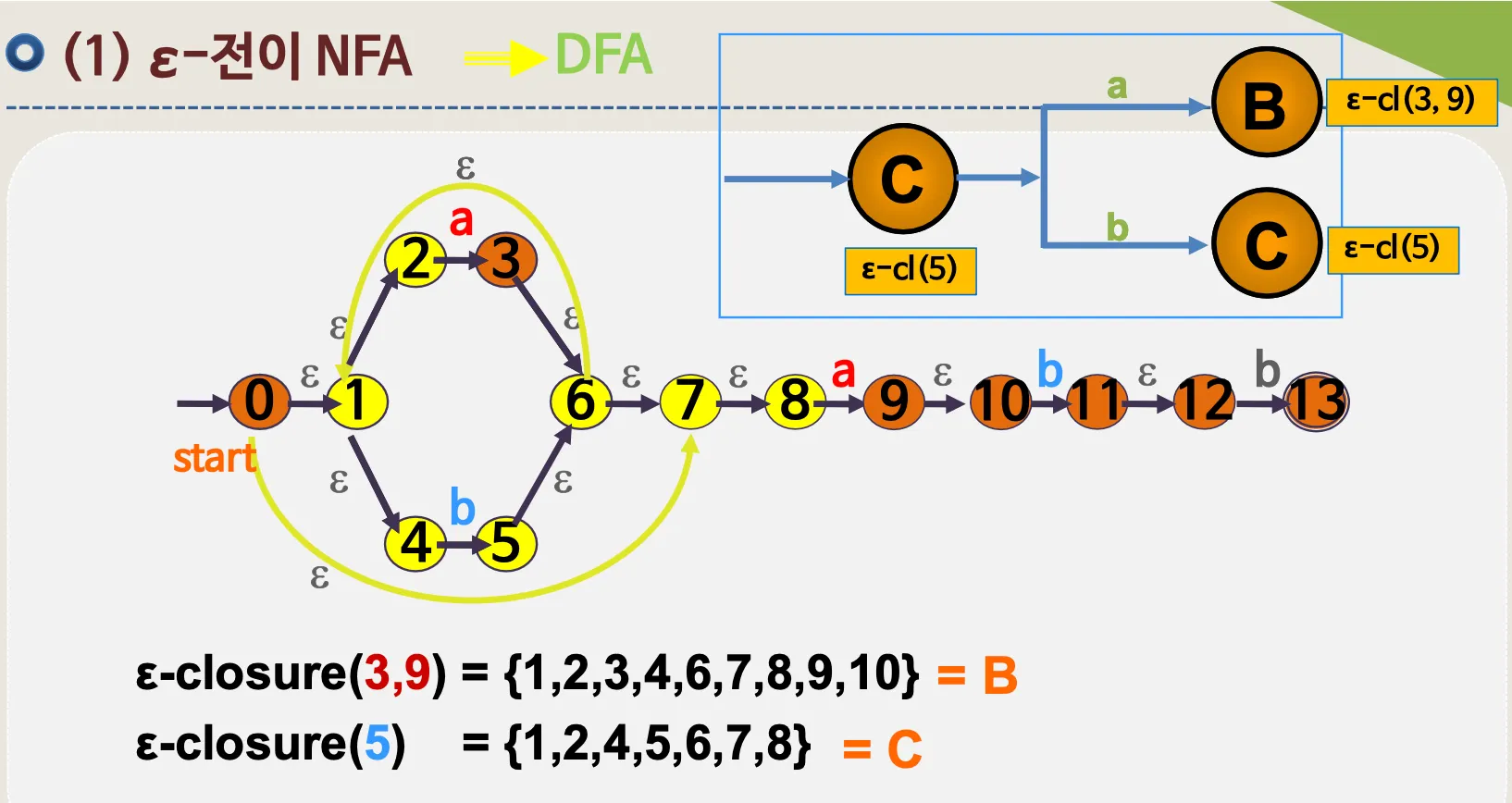
ε–전이 NFA → DFA
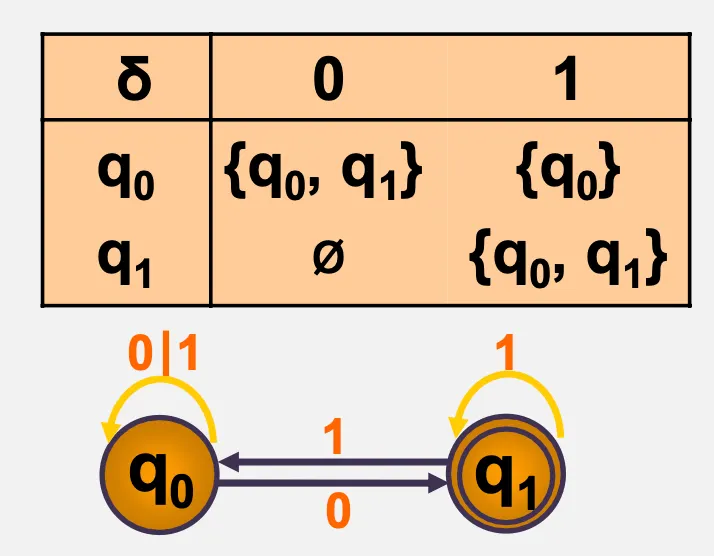
4.2. 2개 이상의 상태전이 NFA
•
M = ({q0, q1},{0,1},δ,q0 ,{q1})
•
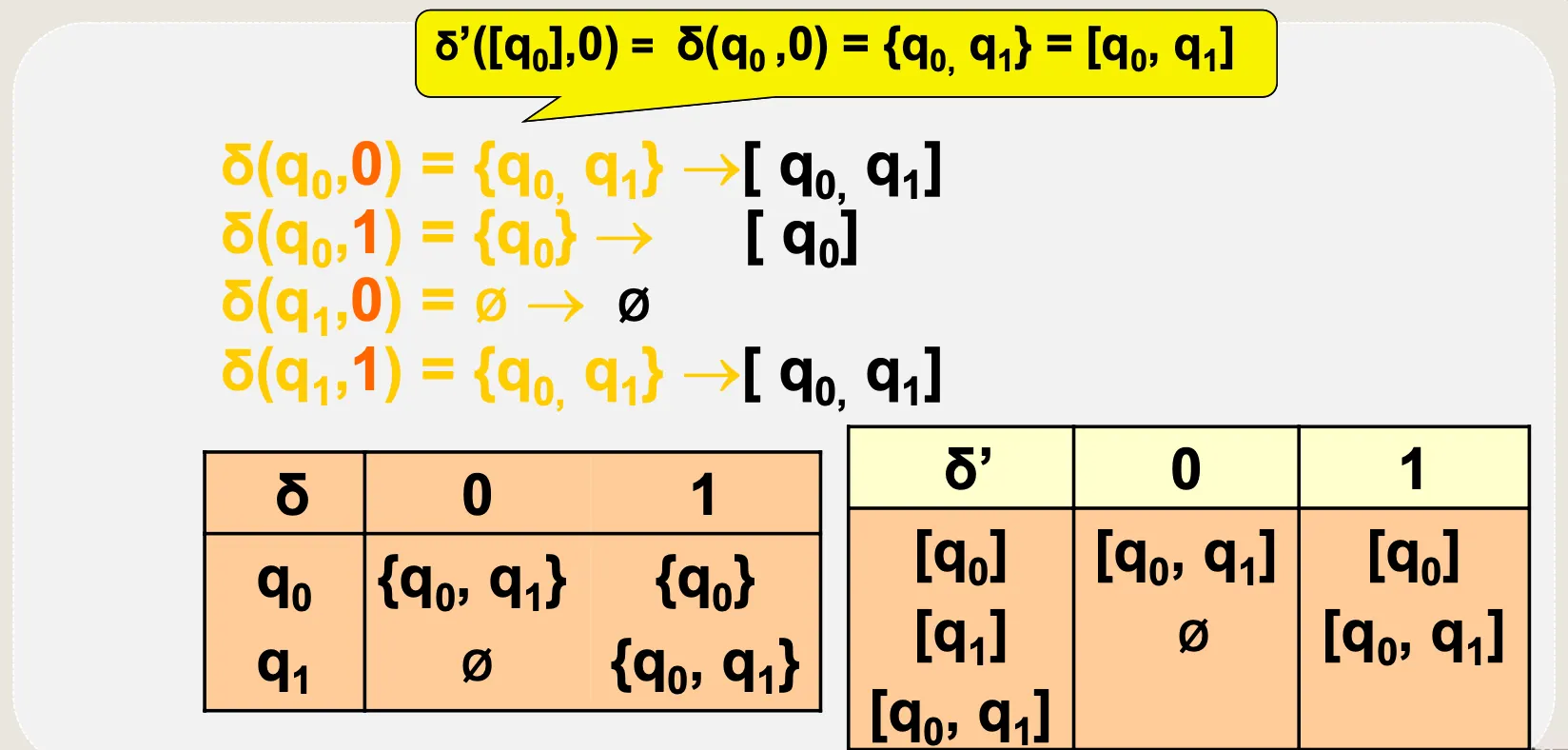
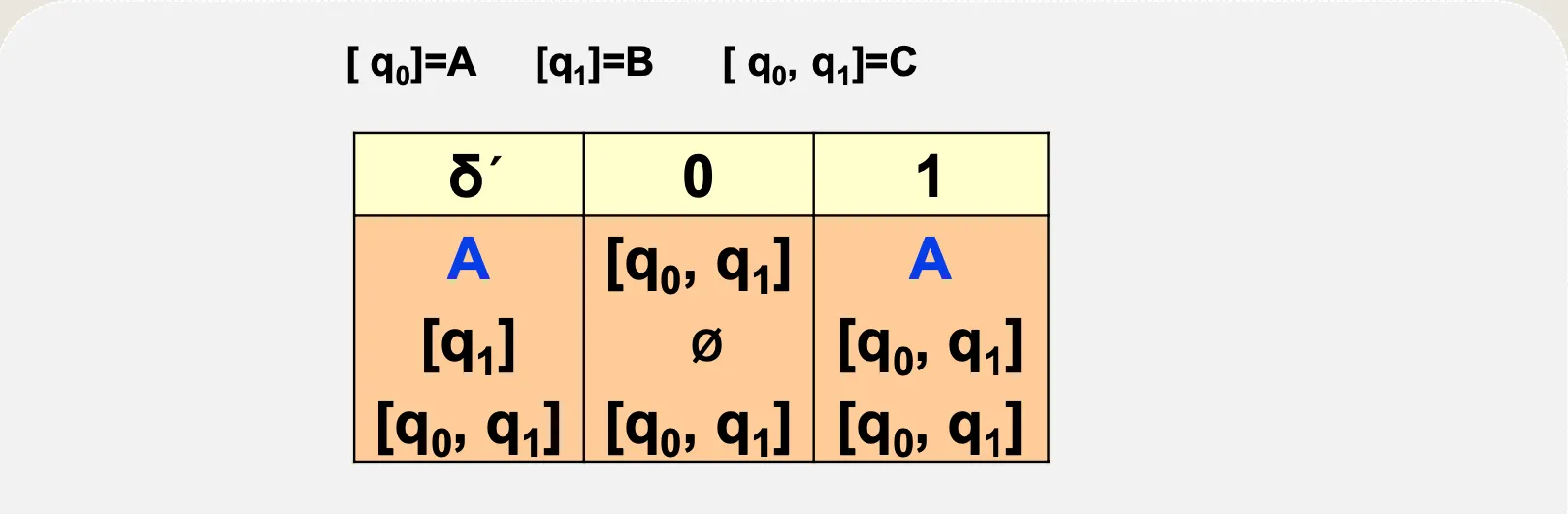
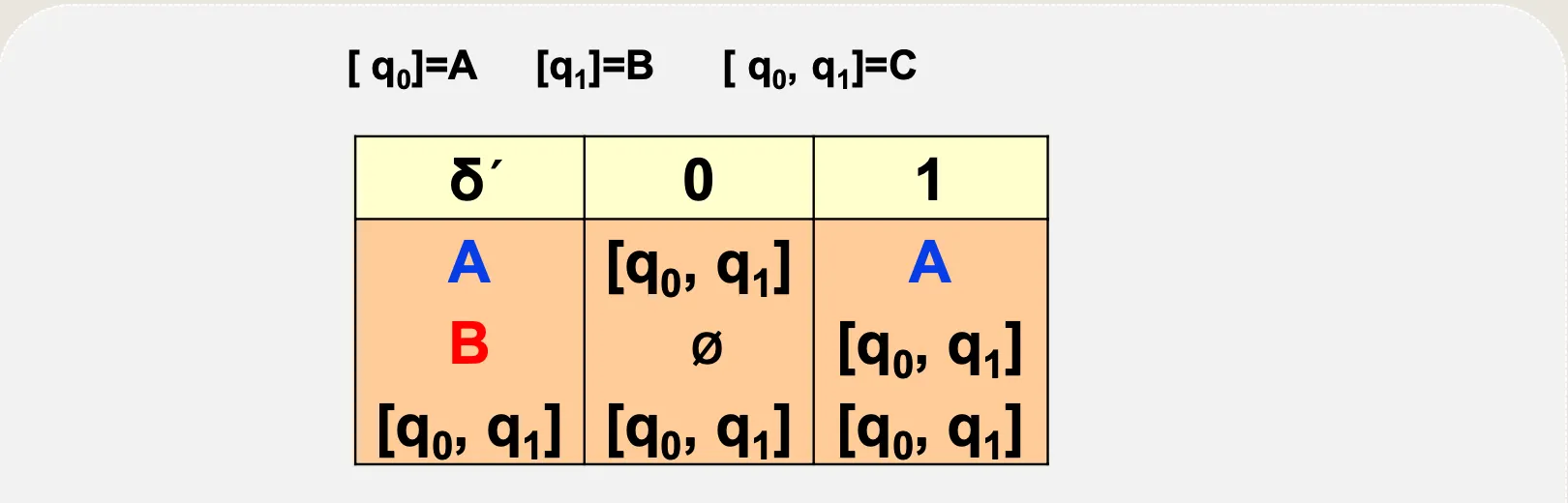
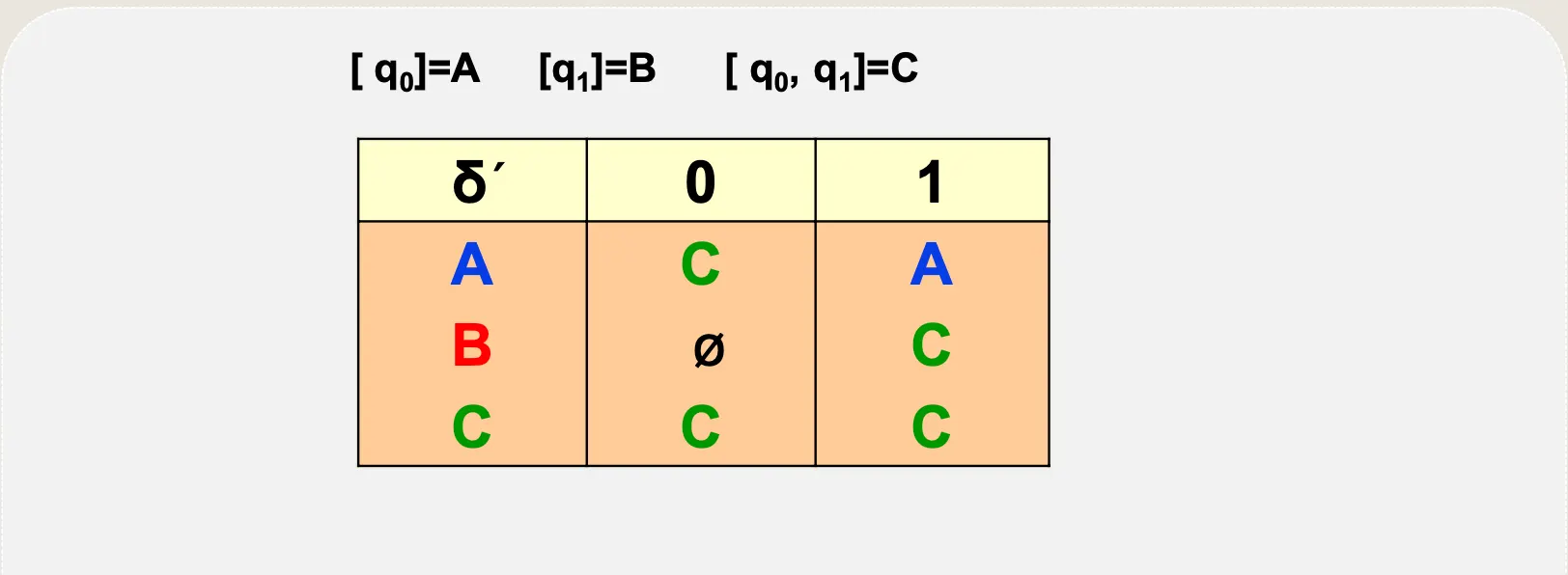
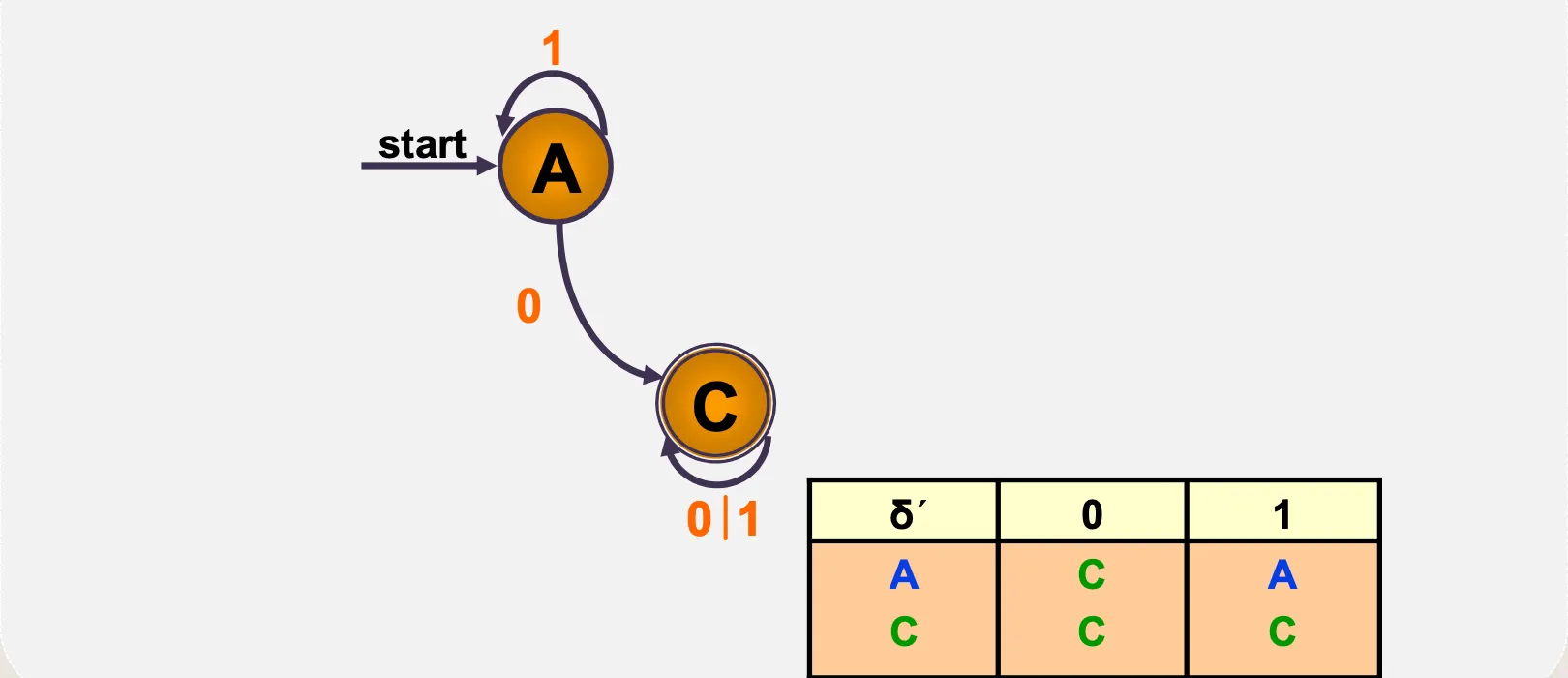
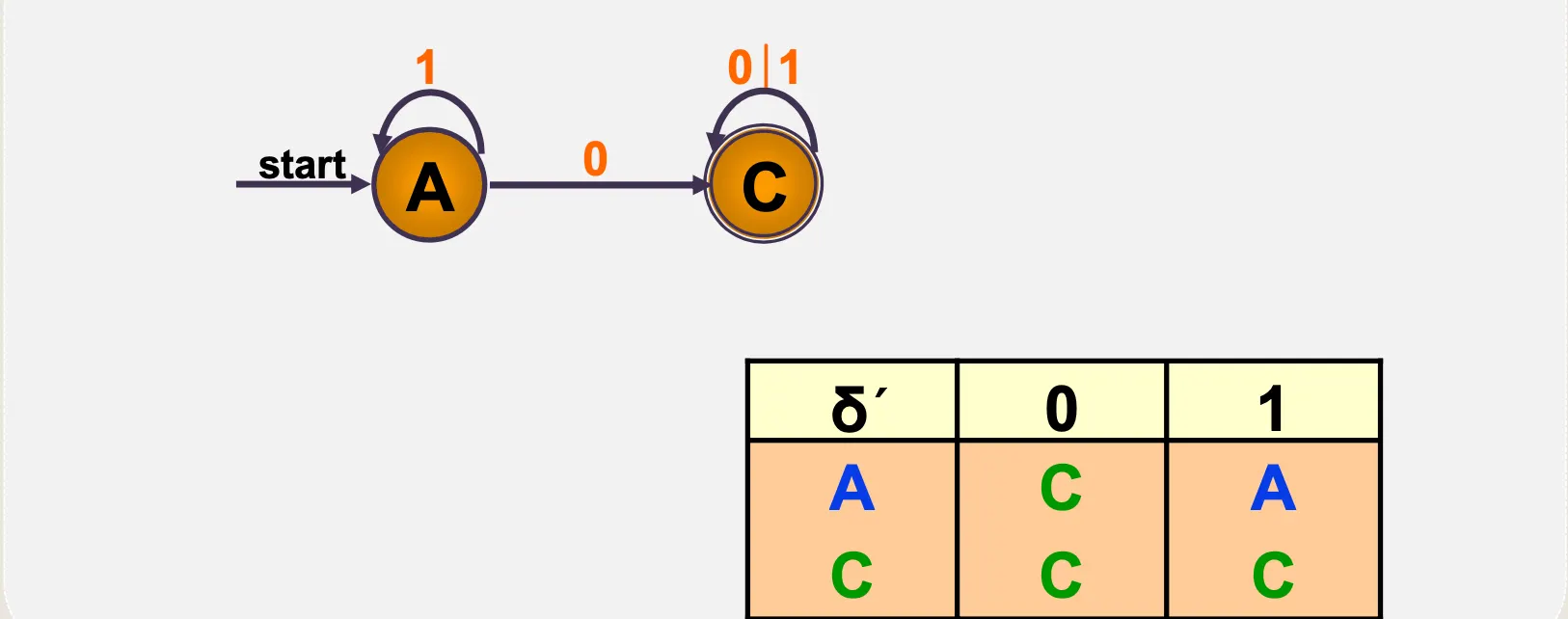
NFA 전이함수표를 DFA 전이함수표로 변화
•
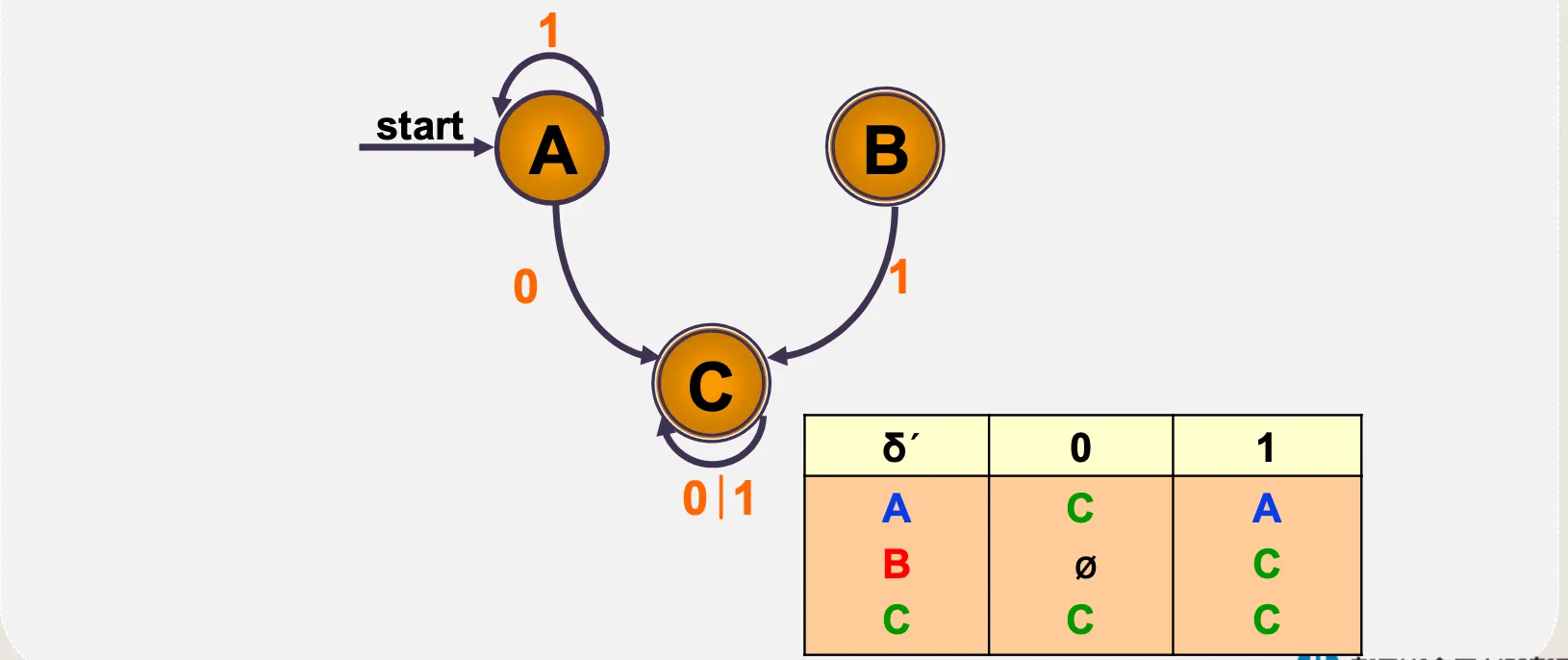
NFA → DFA
◦
110010을 인식하는가? 인식
◦
1111111을 인식하는가? 인식 못함
◦
1111100을 인식하는가? 인식
•
예시2