Total
Search
1. Context-free 언어
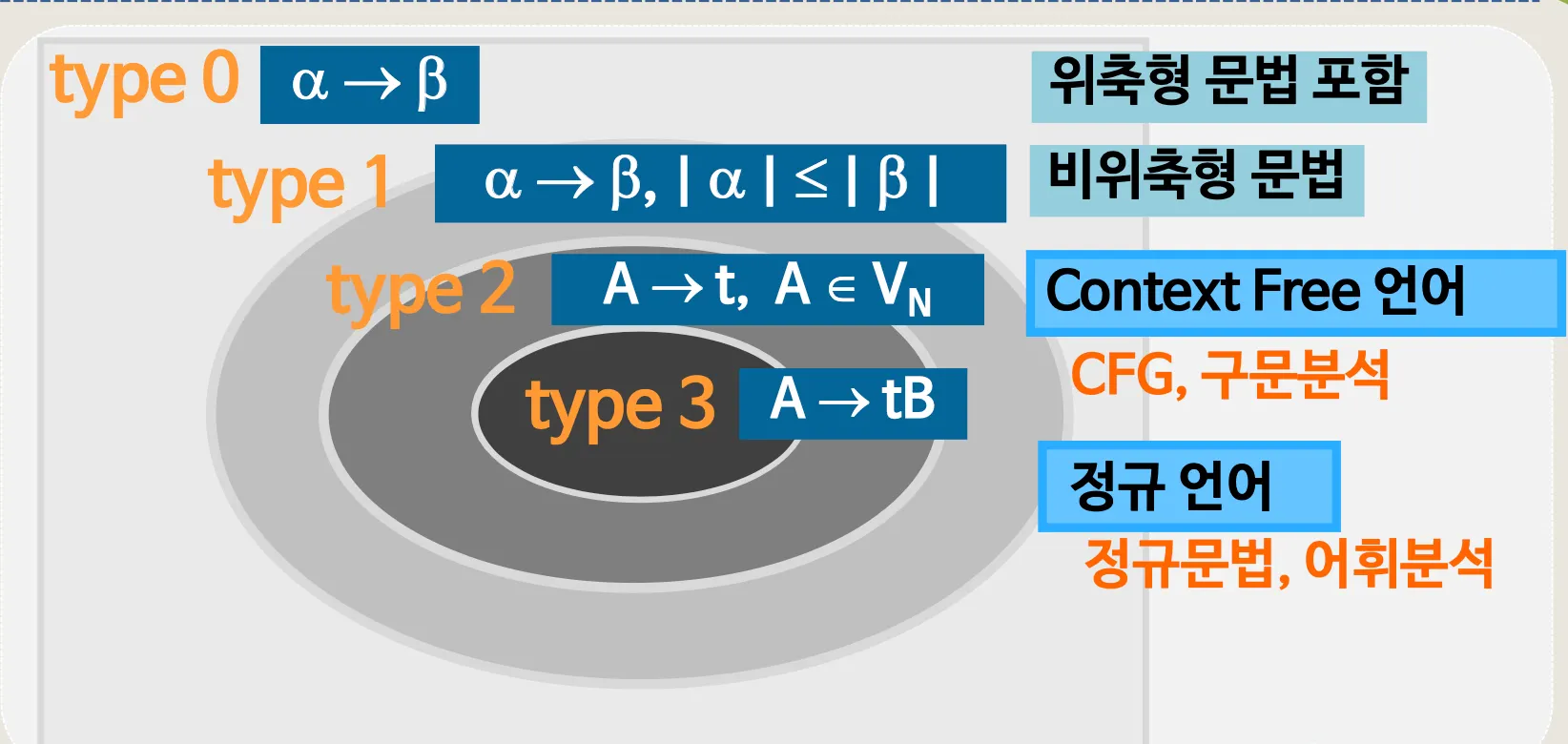
1.1. 문법의 4종류 (chomsky 계층 구조)
•
type3
◦
정규 문법
◦
정규문법에서 Automata가 만들어지면 어휘분석기가 됨
▪
DFA를 구현한 것이 어휘분석기
◦
어휘분석에서 다루는것은 어휘
•
type 2
◦
문장을 정의하고 다루는것은 type2
◦
Context Free 문법
◦
구문분석과 관련됨
1.2. Context-Free 언어
•
IF A=B THEN C:=D ELSE E:=D
•
정규언어: 어휘
◦
IF, A,=, B, THEN, C, :=, D,ELSE, E := D
◦
위의 하나하나가 정규 언어가 됨
◦
정규 언어는 정규문법으로부터 만들어짐 (Type3)
•
Context - Free 언어: 문장
◦
문장은 Context Free Grammar로 정의함
◦
예) IF - THEN - ELSE
◦
이걸 가지고 Automata를 만들어주고 그걸 분석하면 구문분석기가 됨
▪
Push Down Automata
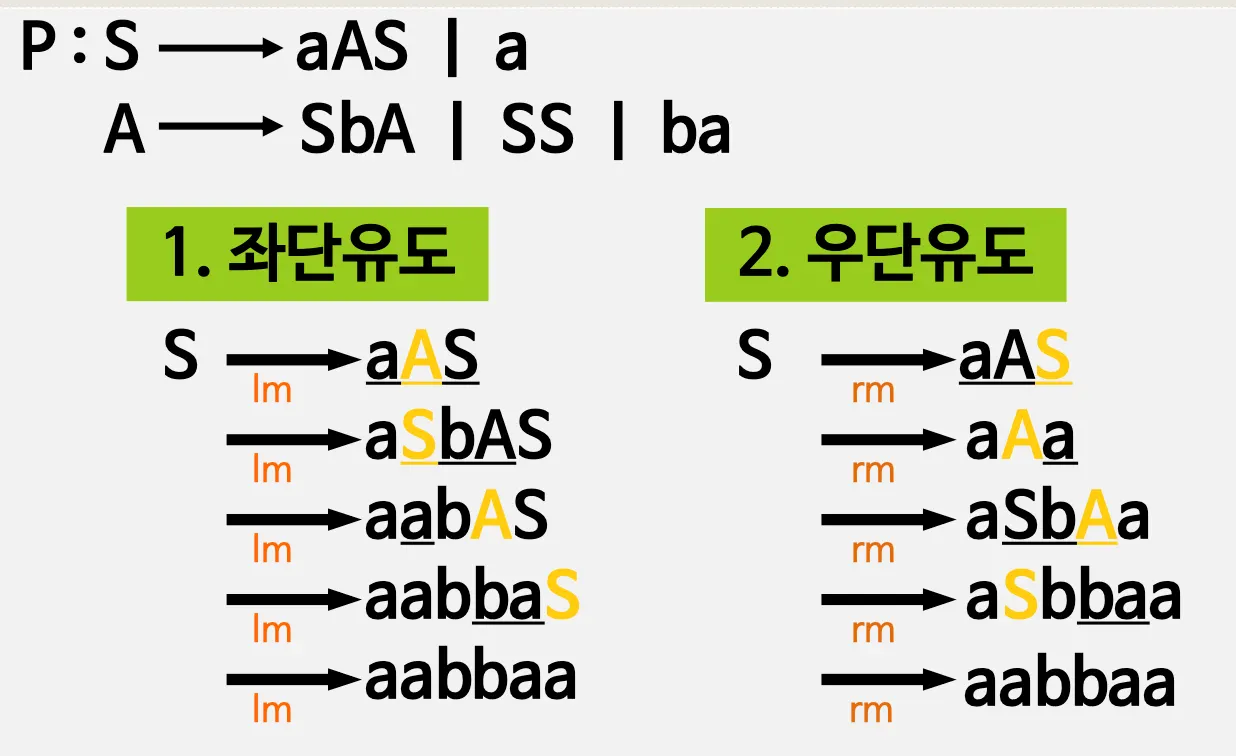
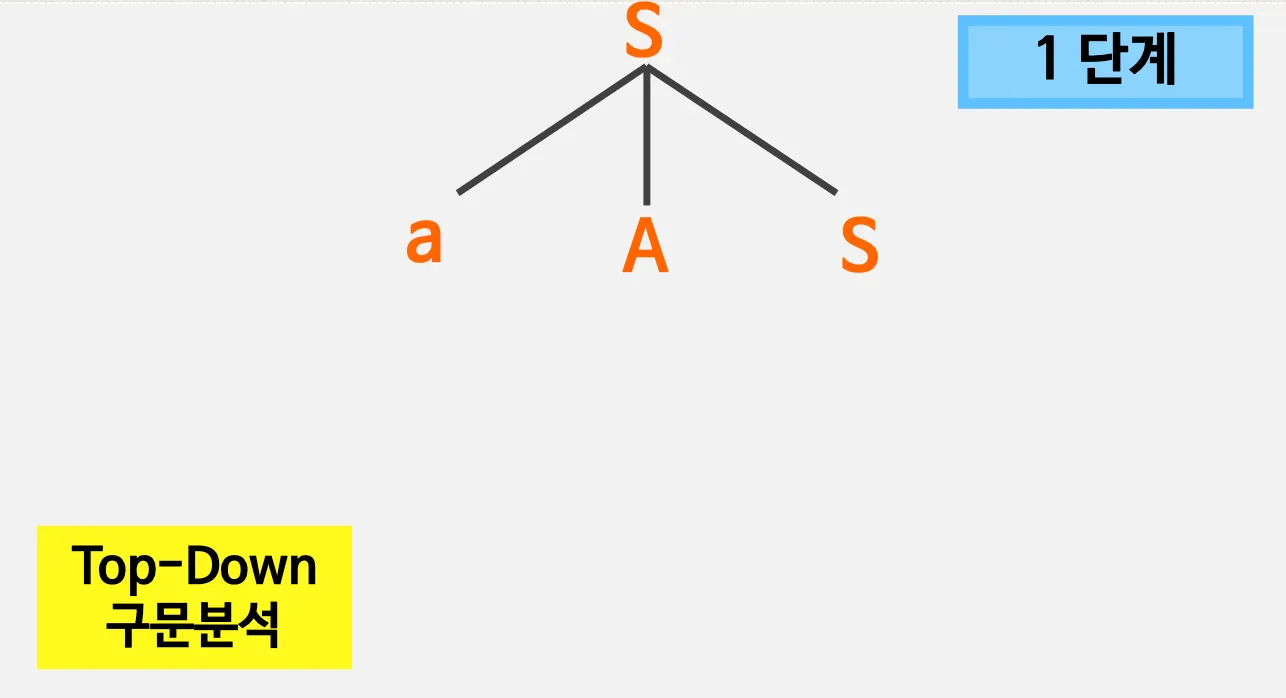
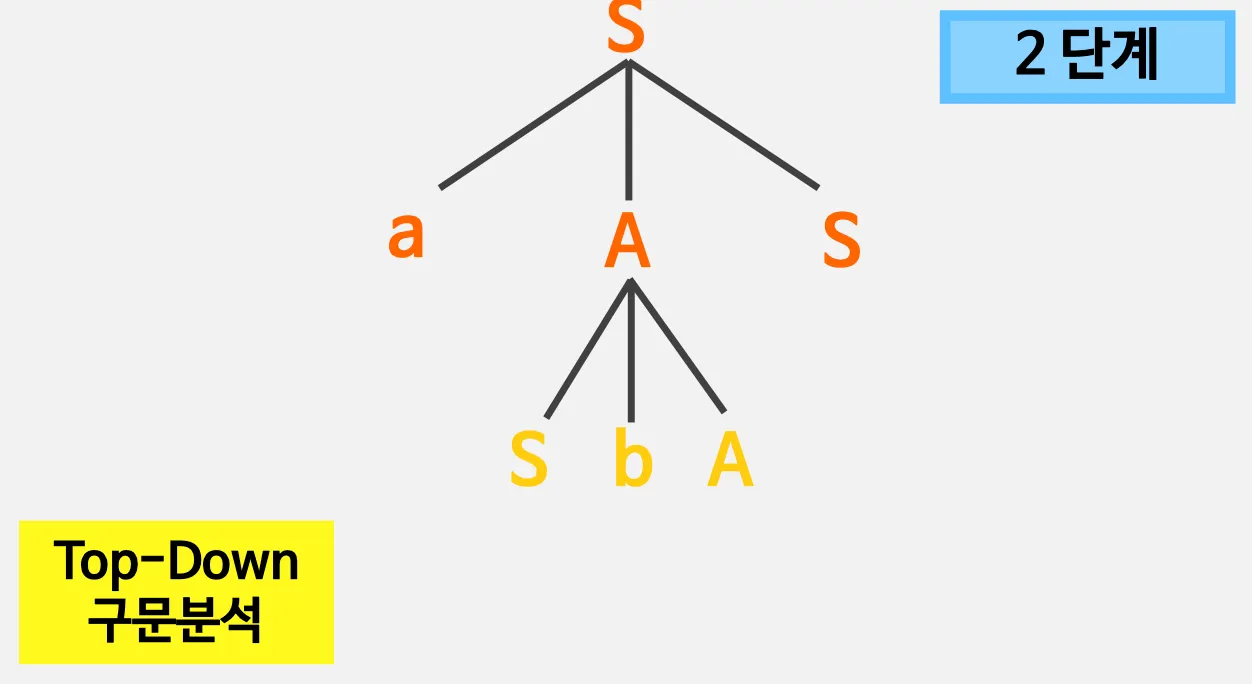
2. 유도트리(derivation)
2.1. 유도 트리
•
좌단 유도
◦
왼쪽을 먼저 유도하는 것
◦
lm: left most
•
우단 유도
◦
오른쪽을 먼저 유도하는 것
◦
rm: right most
•
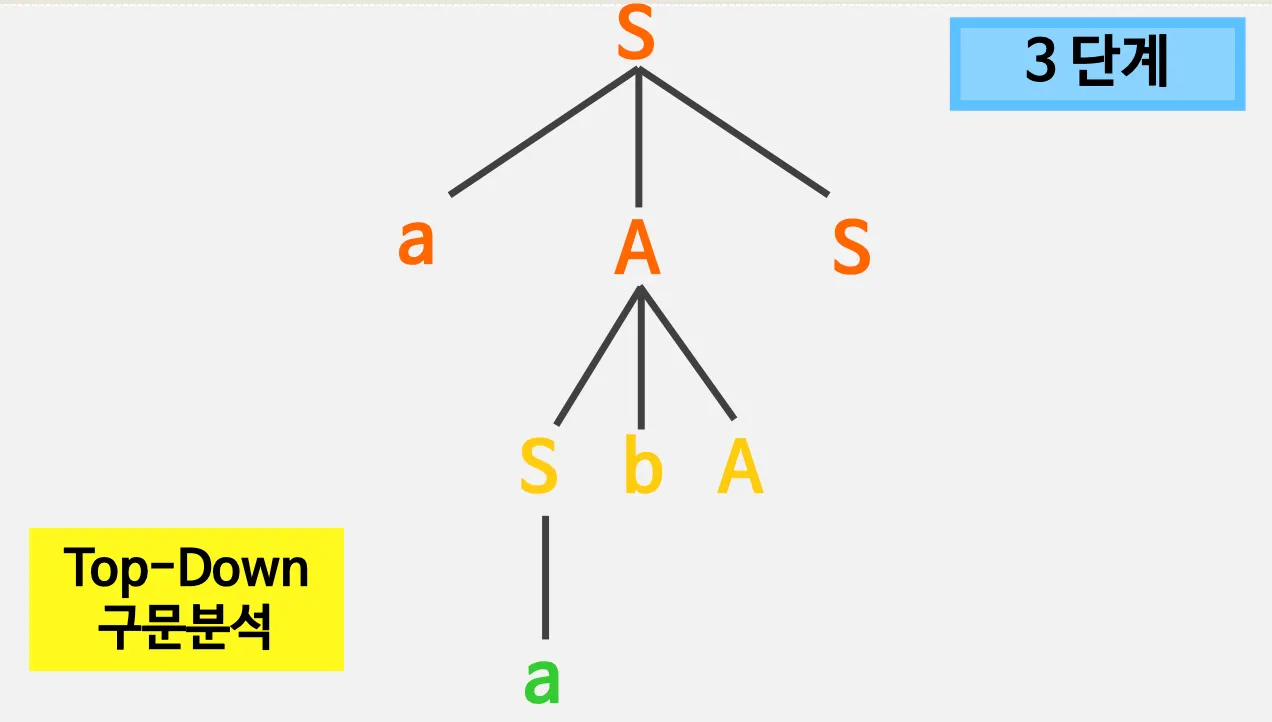
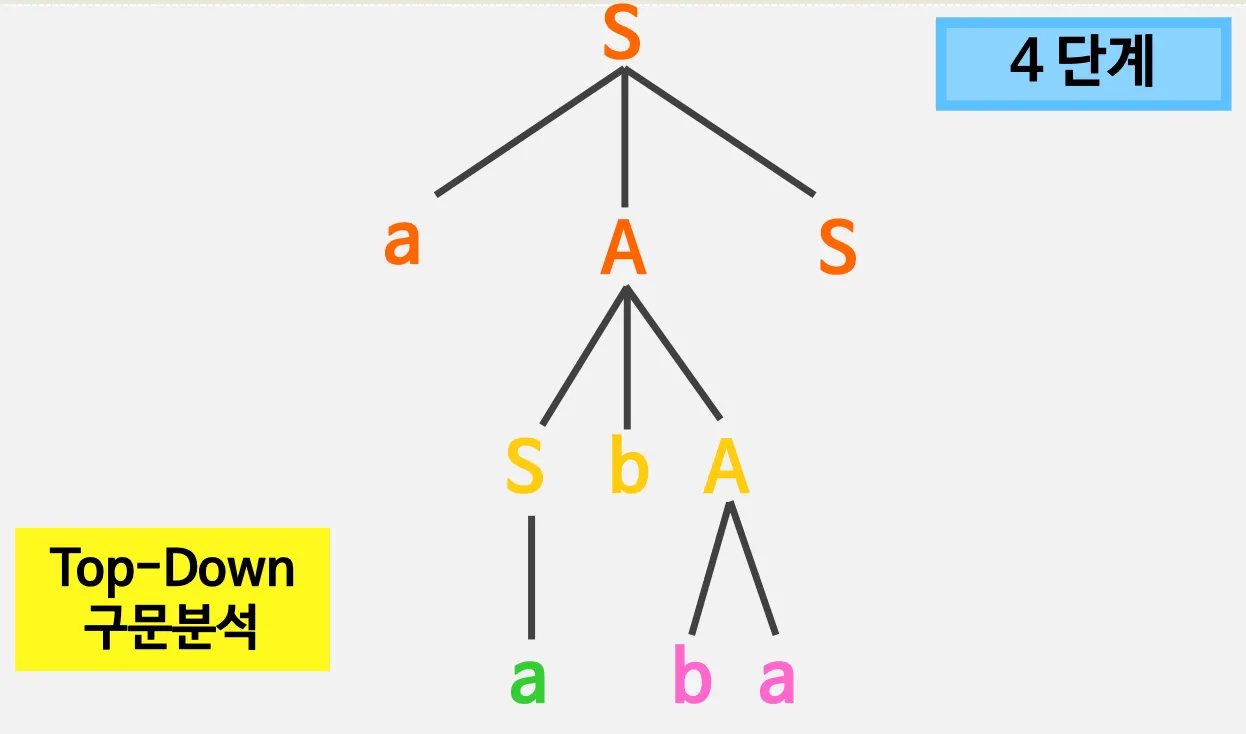
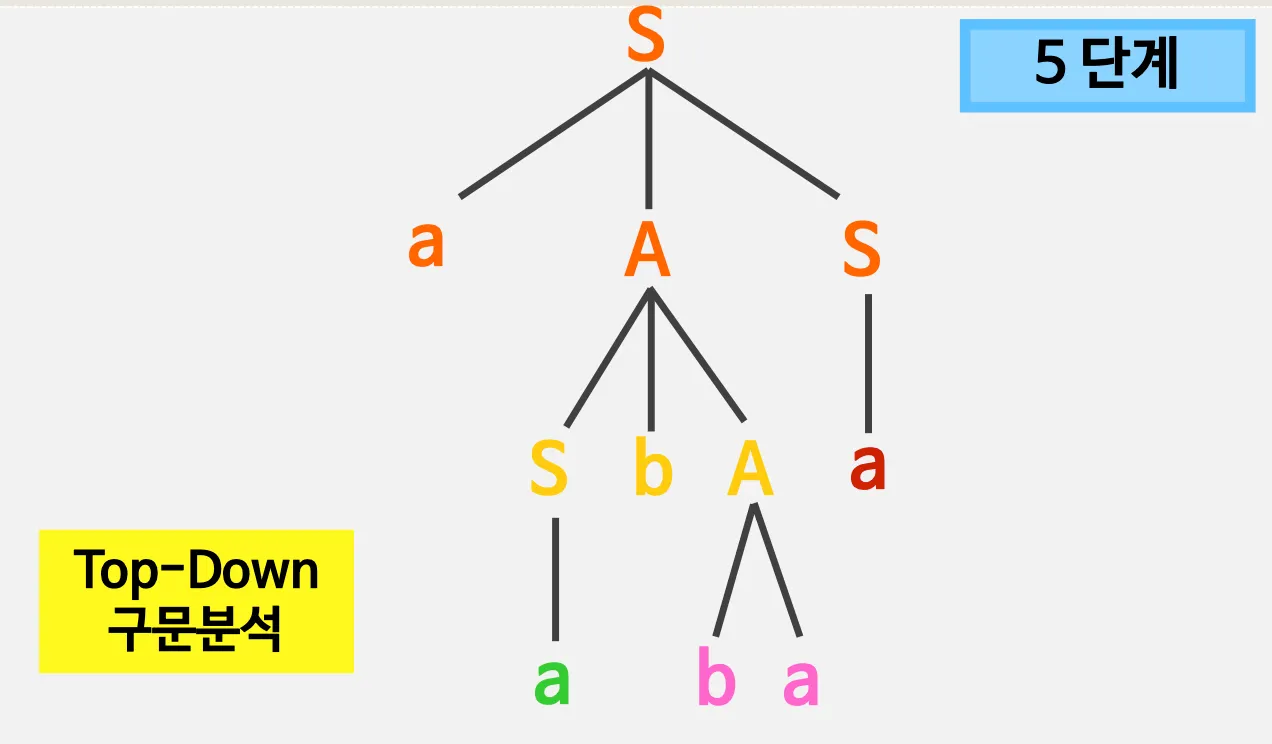
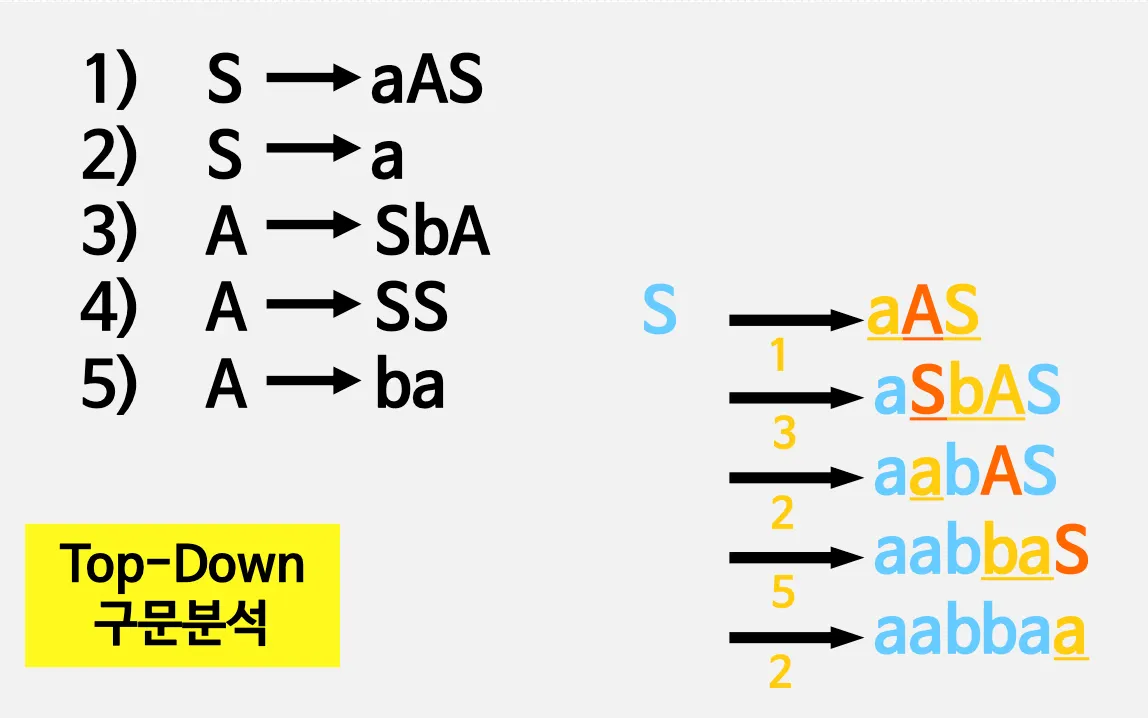
예시)
◦
S, A: non terminal 기호 - 유도가 가능한 기호
2.2. 좌단유도
•
Top - Down 방법
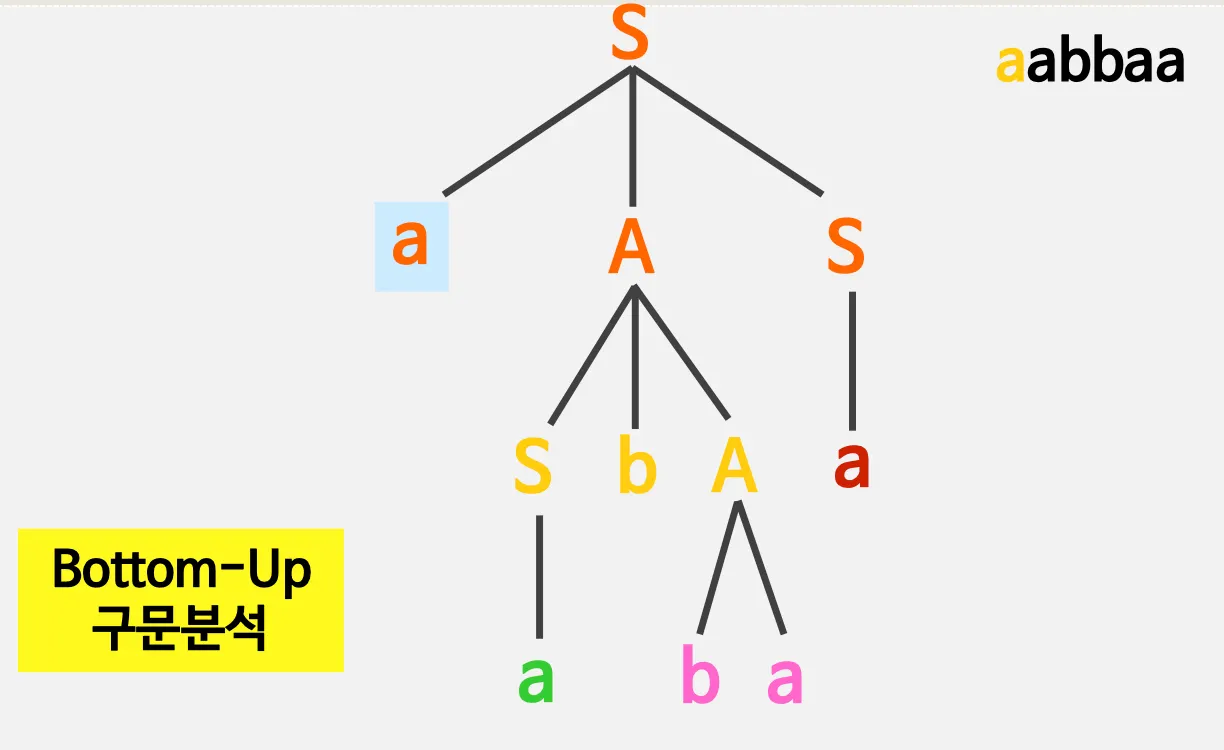
2.3. 우단유도
•
Bottom - Up 방법
•
논터미널 기호 → 터미널 기호가 아니라, 터미널 기호 → 논터미널 기호 순으로 Reduce함 (유도의 반댓말)
•
예)
1.
aabbaa → aSbbaa
2.
aSbbaa → aSbAa
3.
aSbAa → aAa
4.
aAa → aAS → S
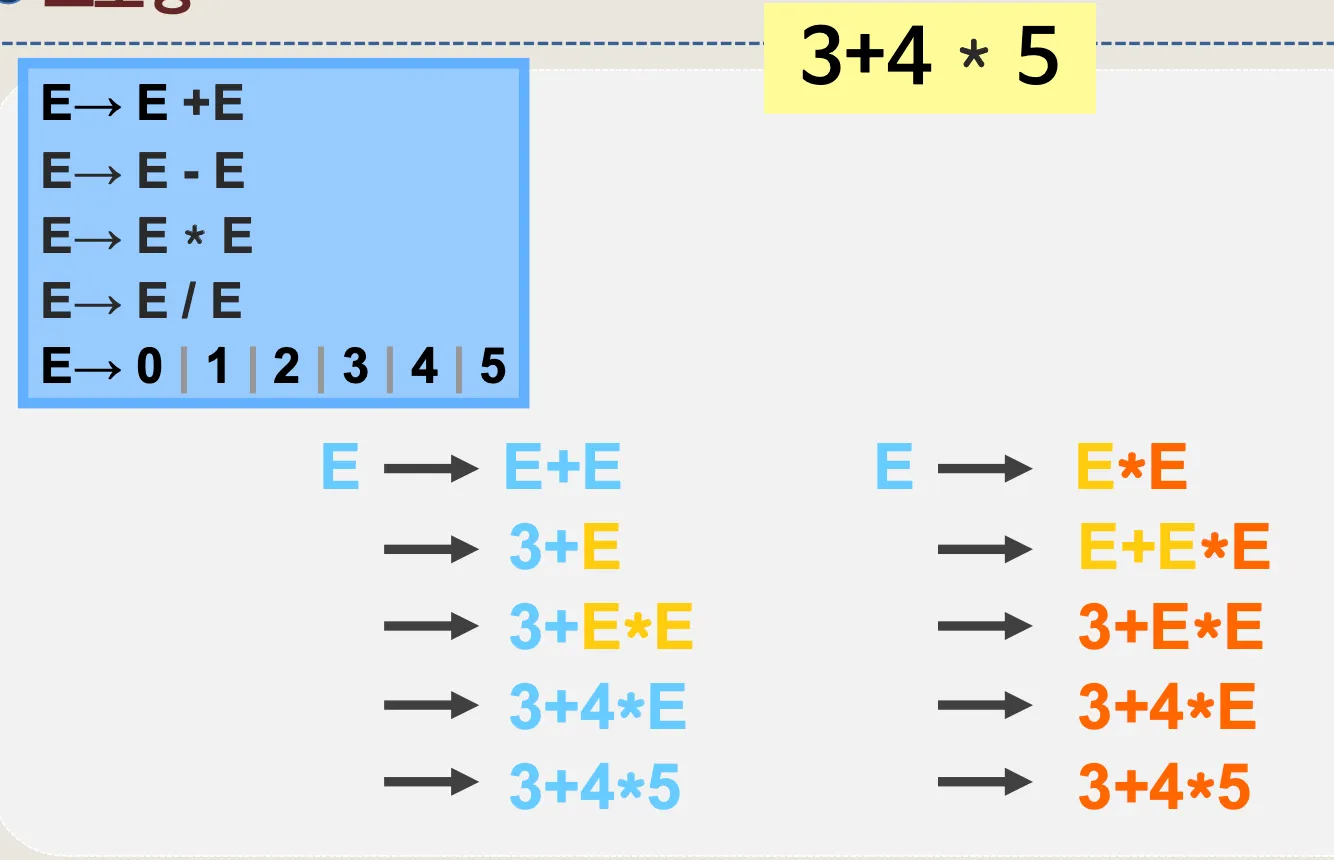
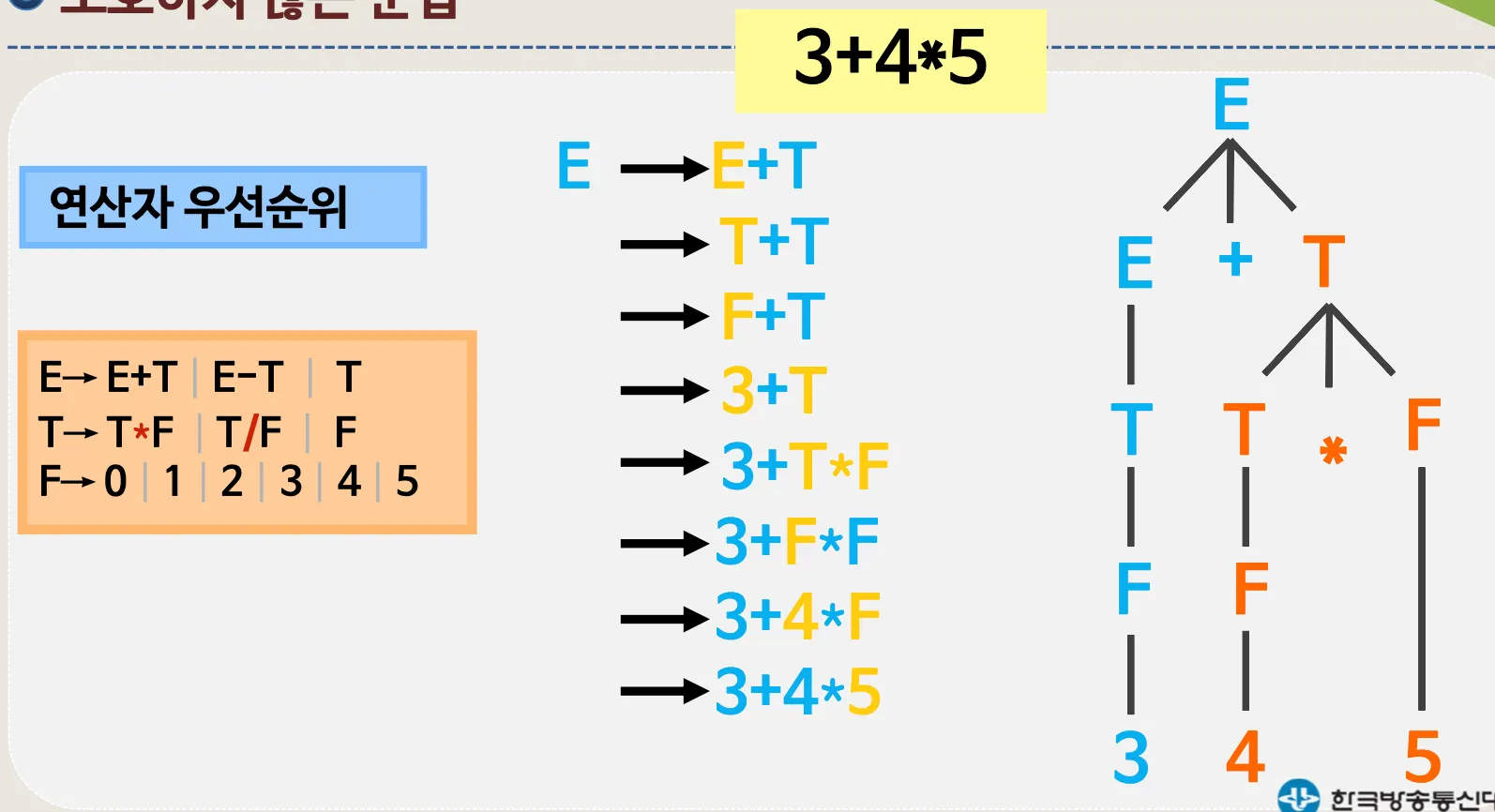
3. 모호성
3.1. 모호성
•
어떠한 문장을 유도하는데 한가지 이상의 길이 있는 경우를 의미
•
여러 경우를 다 고려해야하므로 비효율
•
모호하지 않은 문법으로 변경 필요
•
예시)
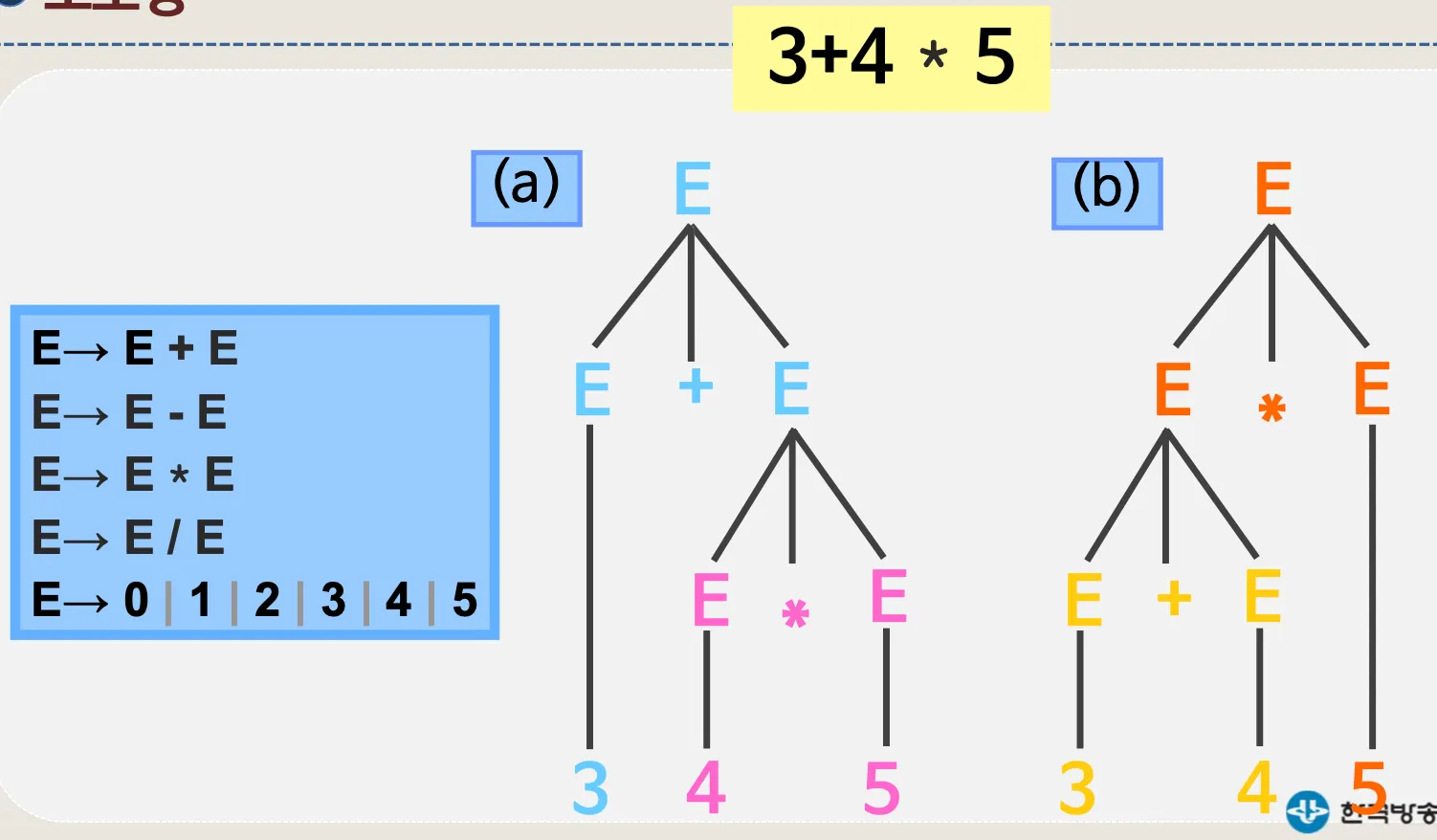
유도 트리로 나타낸 예시
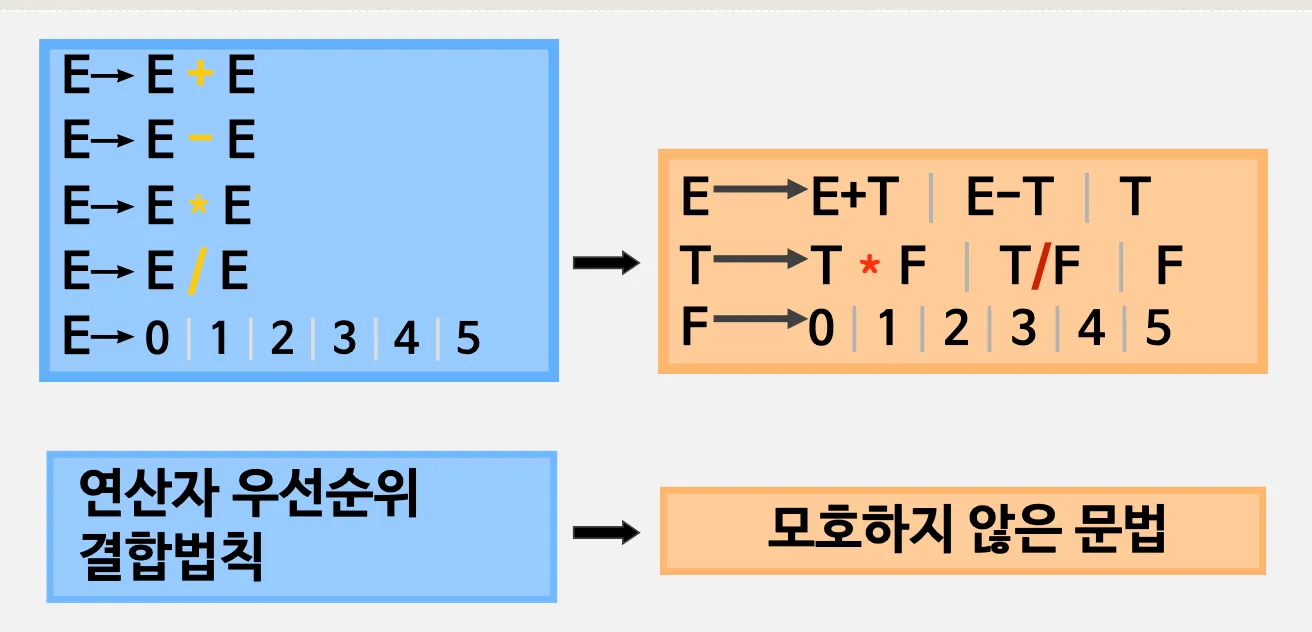
3.2. 모호하지 않은 문법
•
연산자 우선 순위 적용
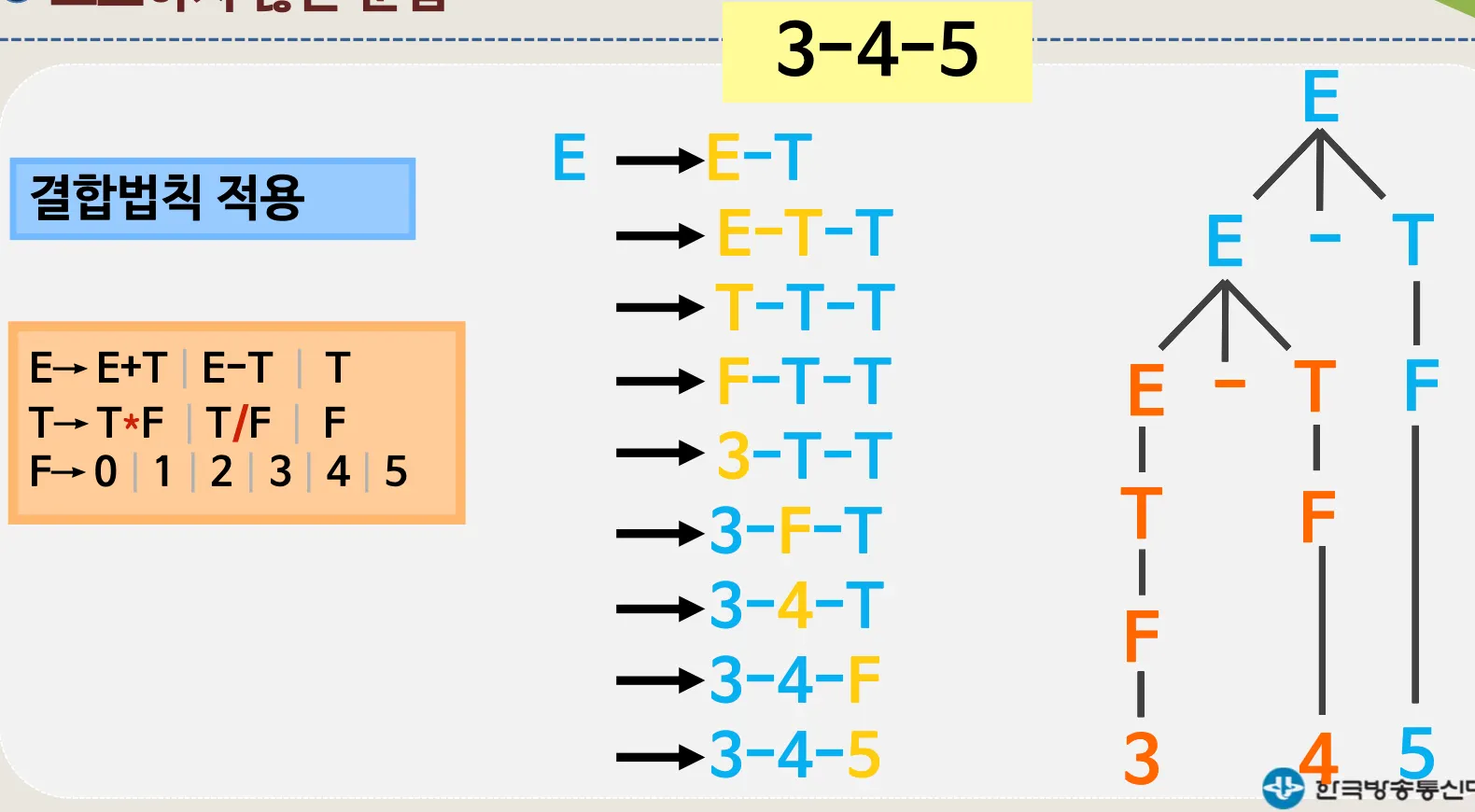
•
결합법칙
•
예시)
연산자 우선순위 적용
결합법칙 적용. 왼편부터
3. CF문법의 효율화
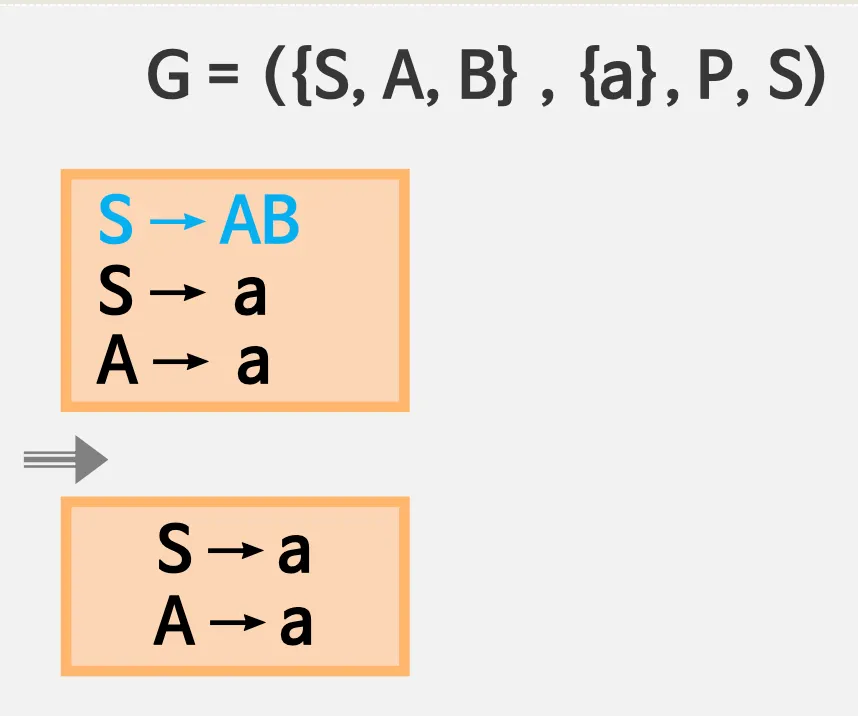
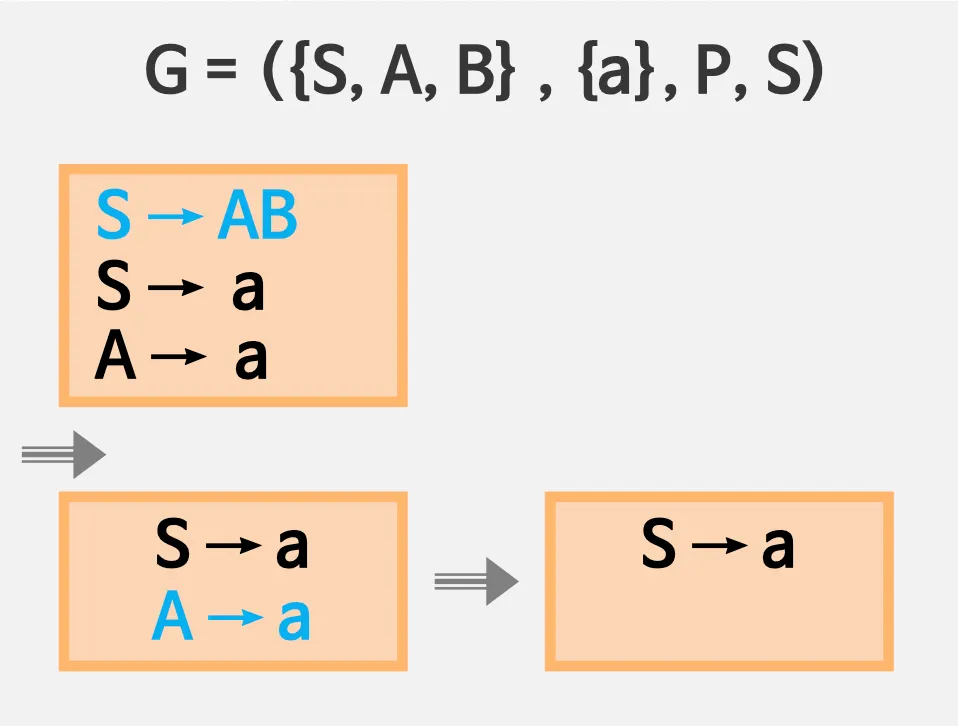
3.1. 불필요한 생성규칙 제거
아래 순서에 맞게 불필요한 생성 규칙 제거 필요
1.
터미널 기호를 생성할 수 없는 논터미널 기호
•
S → AB 제거
2.
시작기호로부터 도달 불가능한 기호
•
시작기호 S인데 A는 도달 불가능함
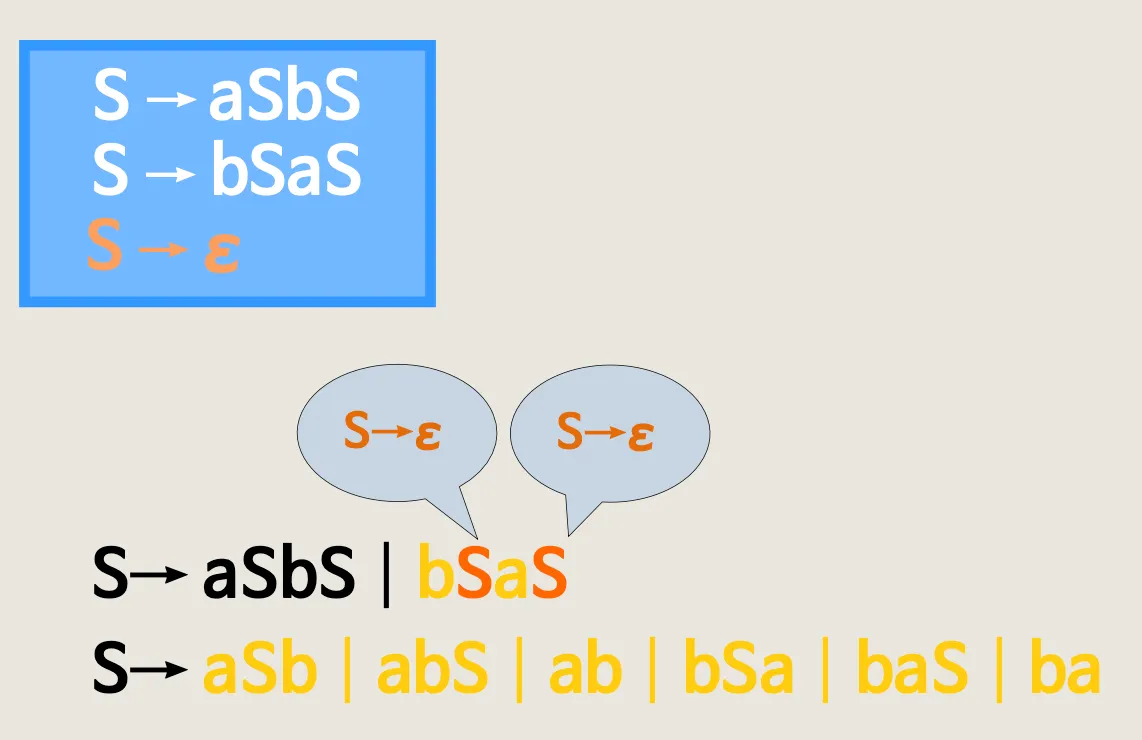
3.2. ε 생성규칙 제거
•
ε 생성규칙의 제거
◦
ε 생성규칙 규칙이 있으면 생성규칙을 적용해봤자 아무것도 없는 것에 불과 → 비효율 발생 → 문법에서 제거하자
◦
ε-free 문법
1.
ε-생성규칙을 갖지 않는다.
2.
시작기호 S → ε 인 경우, 생성규칙의 오른쪽에 S가 없다.
◦
방법
1.
S → ε 대체해서 생성될 수 있는 모든 생성규칙을 P'에 첨가
2.
S' → S ┃ε
•
S’ 라는 시작기호를 새로만들어서 S | ε 를 바라보게 함
•
S 는 아래와 같이 주어주면됨
•
이렇게 수정하면 S에서 곧바로 ε 이 적용될 일이 없어짐
◦
S’ → ε 이 가능하지만 S → ε 규칙은 존재하지 않기 때문
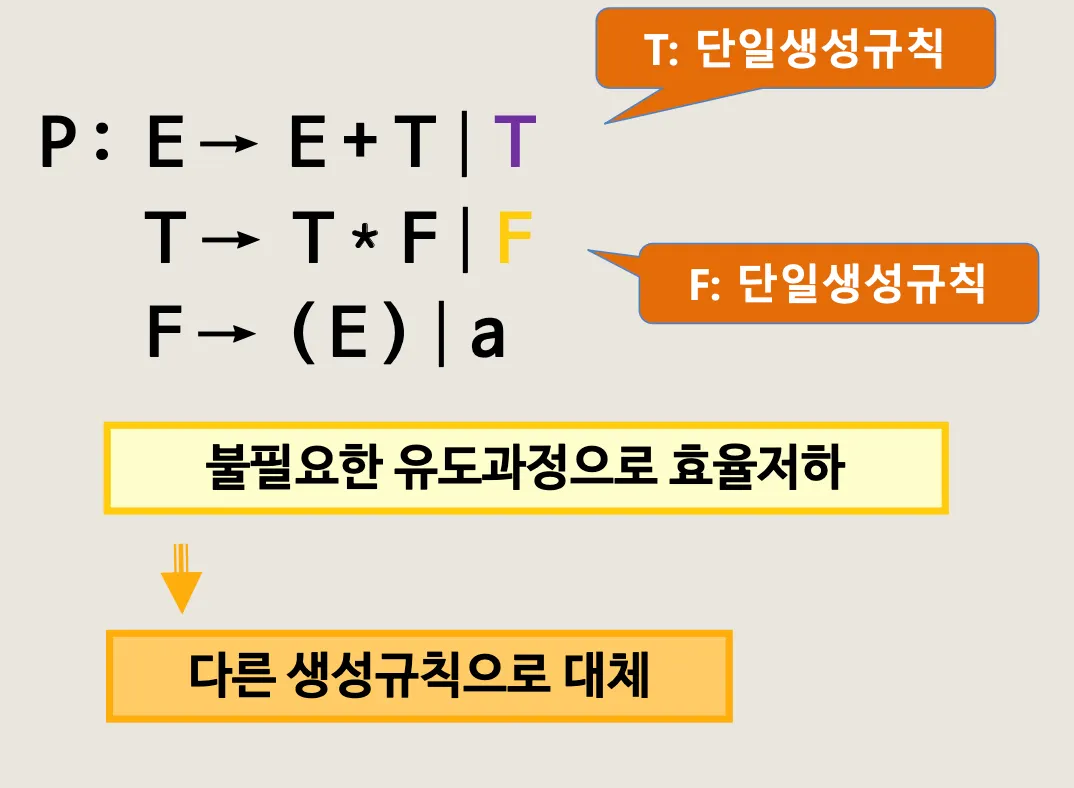
3.3. 단일 생성규칙 제거
•
불필요한 유도 과정을 제거하고 한번만에 유도 할 수 있게 규칙을 생성하자
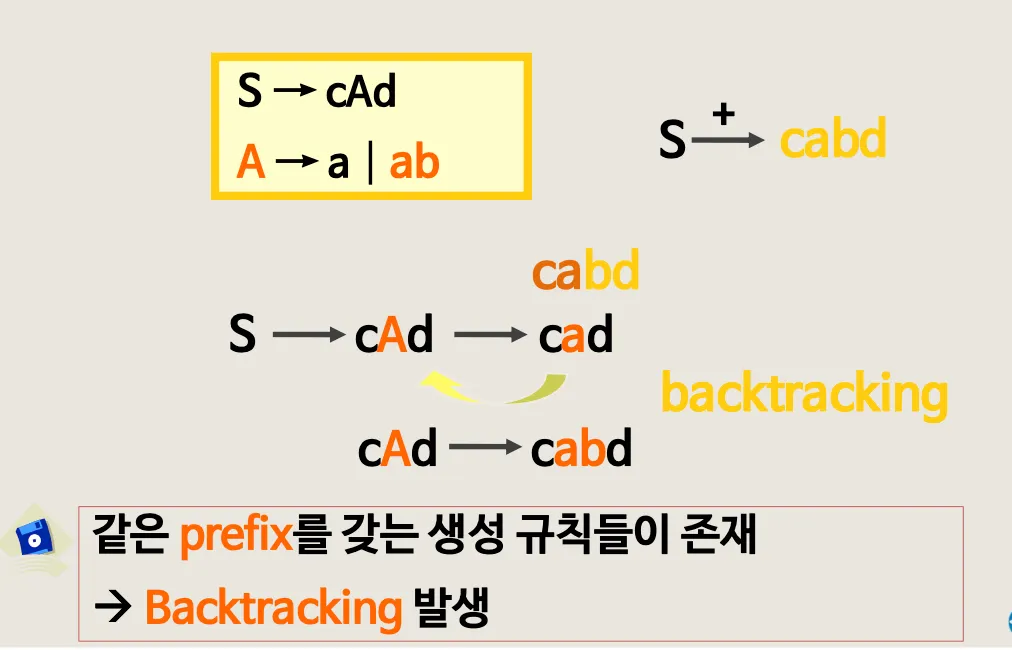
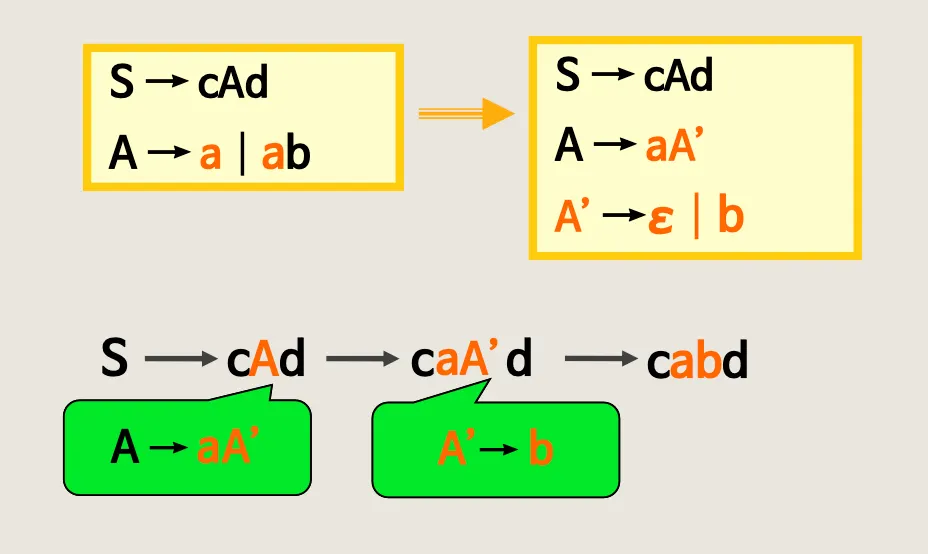
3.4. Backtracking과 Left-factoring (Top-down 구문분석)
•
Backtracking은 컴파일러 효율이 떨어짐 → Left-factoring 적용
•
Left - factoring
◦
공통된 prefix를 인수분해 진행
3.5. Left-recursion 제거 (Top-down 구문분석)
•
생성규칙이 반복적으로 적용
•
무한루프에 빠짐
◦
Right-recursion으로 변환
•
예시)
◦
Left recursion을 Right recursion으로 변경
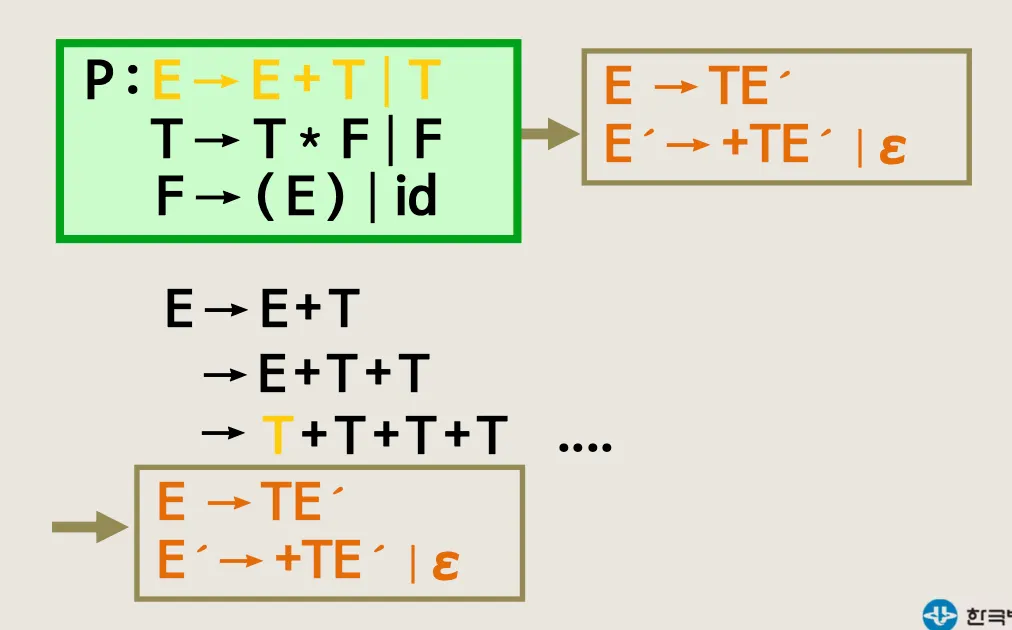
E → E + T | T 변경 예시
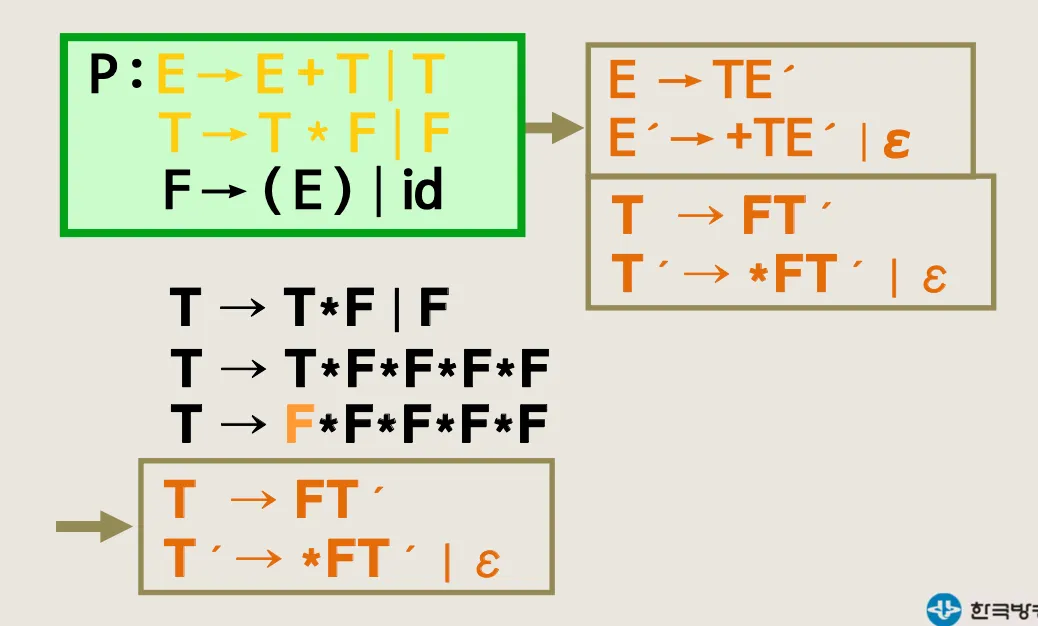
T → T * F | F 변경 예시
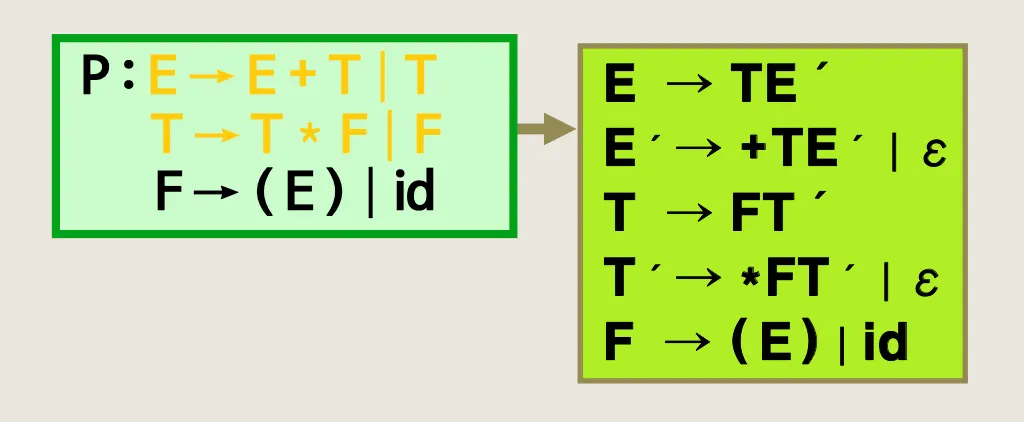
최종 결과
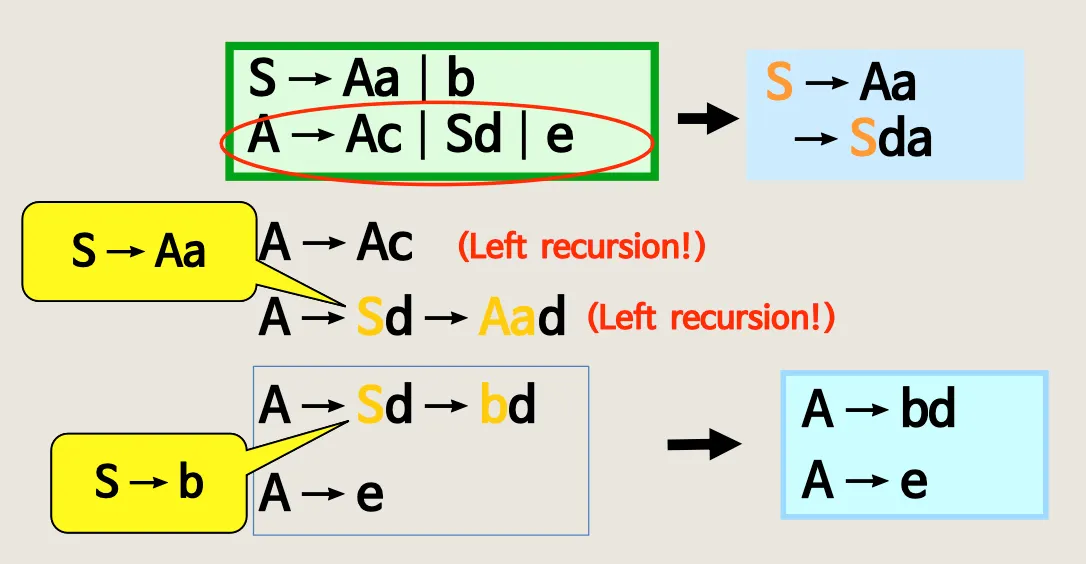
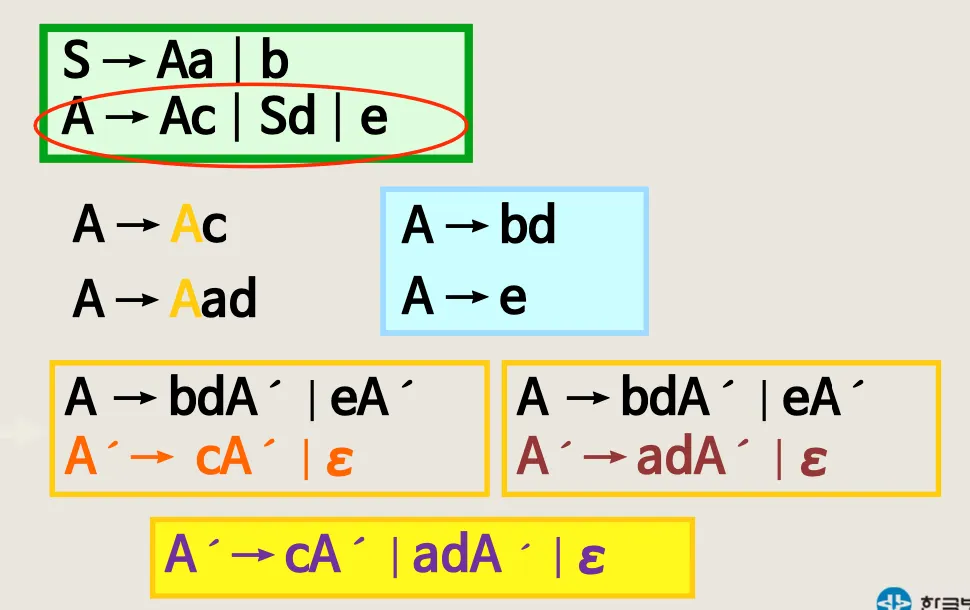
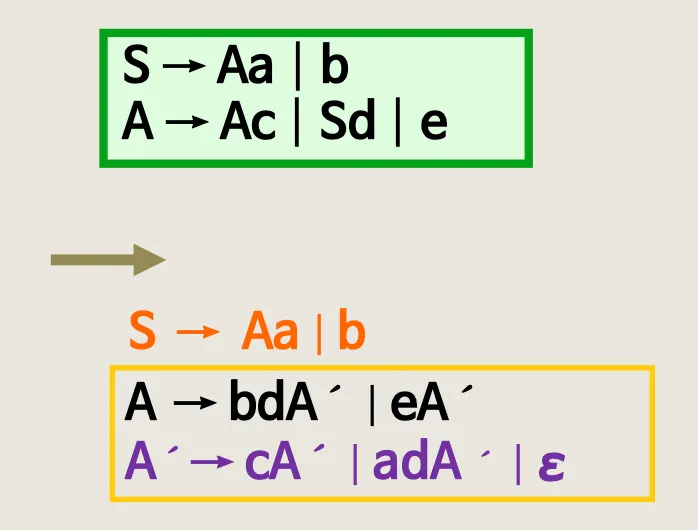
•
간접 Left - recursion
최종 정리 버전
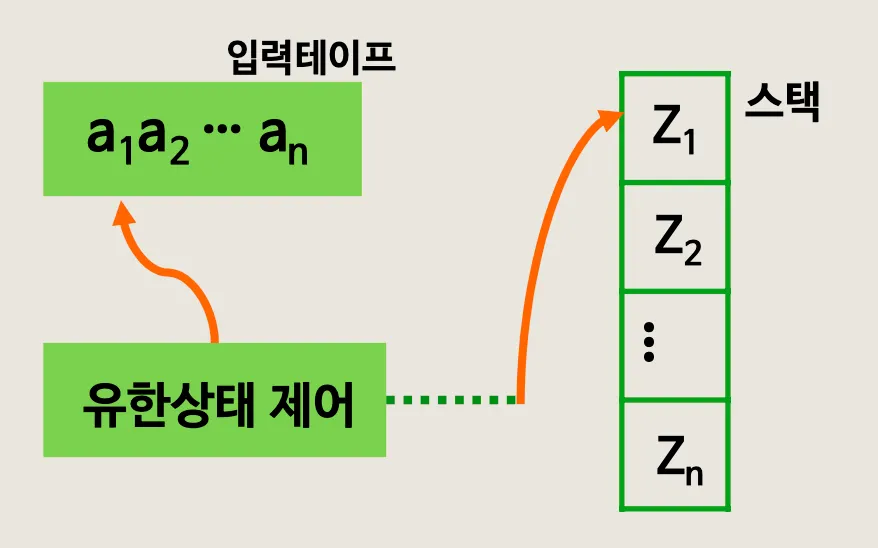
4. Push-down Automata
4.1. Push-down Automata
•
예시
•
PDA 정의
◦
M = (Q, Σ, T, δ, q0, z0, F)
▪
Q : 상태들의 유한집합
▪
Σ : 입력 기호들의 유한집합
▪
T : 스택 기호들의 유한집합
▪
q0 ∈Q : 시작상태(start state)
▪
z0 ∈T : 스택의 시작기호
▪
F ⊆Q : 종결상태의 집합
▪
δ : 사상함수 Q×(Σ∪{ε})×T → Q×T*