Total
Search
1. 시뮬레이션
1.1. 시뮬레이션의 정의
•
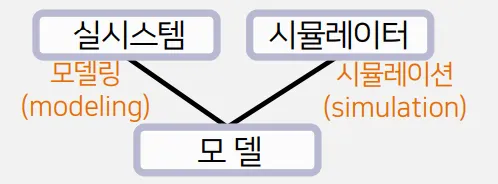
실제 시스템에서 실시스템의 성질을 나타내는 모델을 만들고 그 모델로 실험하는 것
1.2. 시뮬레이션의 기본 요소
•
실 시스템
◦
우리가 관찰하고자 하는 대상
•
시뮬레이터
◦
시뮬레이션 프로그램을 실행하는 기계로 주로 컴퓨터
•
모델
◦
실 시스템을 모방한 것
•
cf) 모델링
◦
실시스템의 형태를 모방한 모델을 만드는 과정
1.3. 시뮬레이션의 목적 및 특징
•
목적
◦
실제 시스템의 행위를 모델링하고 이를 통해 예측, 평가, 분석, 훈련
•
특징
◦
미래 예측
▪
시뮬레이션을 통해 미래의 결과를 예측
◦
시간 변수 사용 및 다양한 실험 가능
▪
시뮬레이션은 시간에 따라 변화하는 변수와 다양한 실험을 통해 결과를 도출
1.4. 시뮬레이션의 구분
•
확률 변수 (random variable)의 사용 여부
◦
결정적(확정적) 시뮬레이션 (deterministic simulation)
◦
확률적 시뮬레이션 (probabilistic simulation)
▪
확률적 시뮬레이션에서는 변수 값이 불확실함
▪
우리가 일반적으로 생각하는 시뮬레이션
2. 결정적 시뮬레이션 (deterministic simulation)
2.1. 결정적 시뮬레이션의 정의 및 특징
•
정의
◦
동일한 입력 조건과 매개변수에 대해 항상 동일한 결과를 산출하는 시뮬레이션
•
특징
◦
확률 변수나 무작위 요소가 사용되지 않음
◦
입력 값이 정해지면 그에 따른 출력 결과도 미리 예측할 수 있음
2.2. 결정적 시뮬레이션의 예시
•
결정적 시뮬레이션이 사용되는 경우
◦
시스템의 동작이 명확하고 불확실성이 거의 없는 경우
◦
결과를 정확하게 예측하거나 최적화할 때
◦
분석과 실험 결과를 반복해서 재현할 필요가 있는 경우
◦
변수가 특정 값으로 고정되어 있음
•
저축 문제
◦
연봉 상승 및 저축 계산
▪
매년 연봉이 5% 상승하고, 저축액은 연봉의 10%, 은행 이율 5%로 복리 계산.
◦
결과
▪
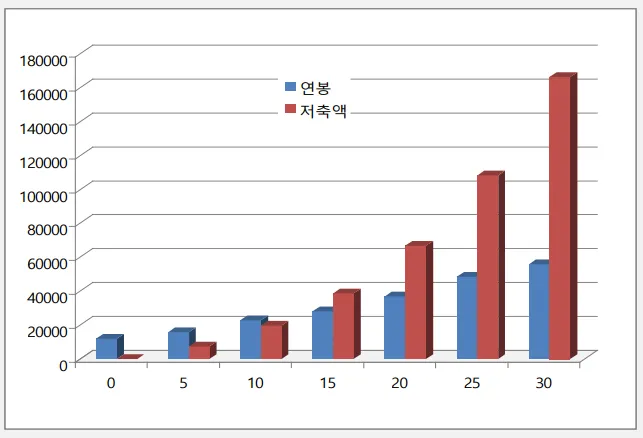
30년 후의 연봉과 저축액을 그래프로 시각화
•
공의 탄성 문제
◦
중력 가속도 및 반동
▪
공이 튀면서 속도가 매번 25% 감소.
◦
알고리즘
▪
초기 속도와 각도를 설정하고, 중력과 반동을 계산하여 공의 위치를 추적.
3. 확률적 시뮬레이션 (Probabilistic Simulation)
3.1. 확률적 시뮬레이션의 정의
•
시스템이나 과정에서 발생할 수 있는 불확실성을 반영하기 위해 확률 변수를 사용하여 여러 가능한 시나리오와 결과를 모사하는 시뮬레이션 기법
•
확률 변수를 사용하여 불확실성을 포함한 시뮬레이션
•
변수들이 일정한 확률 분포에 따라 무작위로 선택되므로 동일한 입력 조건에서도 매번 다른 결과가 나올 수 있음
3.2. 확률 분포의 정의
•
확률변수 X 가 특정한 값을 가질 확률을 나타내는 분포로 X의 함수
•
확률 변수가 취할 수 있는 모든 가능한 값과 그 값들이 발생할 확률을 정의한 함수나 규칙
3.3. 확률 분포의 종류
•
일양 분포 (Uniform Distribution)
◦
모든 값이 동일한 확률로 발생 (균등 분포)
◦
예) 승객들이 전철역에 도착해서 기다리는 시간 (전철 간격 7분)
▪
어떤 구간이든 동일한 확률을 가짐 (연속형 일양 분포)
•
정규 분포 (Normal Distribution)
◦
평균과 표준편차로 표현되는 분포
◦
예) 시뮬레이션 성적 분포
•
지수 분포 (Exponential Distribution)
◦
독립적인 사건들이 발생하는 간격을 설명
◦
예) 은행에 도착하는 고객의 도착시간 간격
•
포아송 분포 (Poisson Distribution)
◦
일정 시간 내에 발생하는 사건 수를 설명
◦
예) A회사의 단위 시간당 전화문의
3.4. 난수
•
정의
◦
특정 패턴이나 규칙 없이 무작위로 생성된 숫자를 의미
•
특징
◦
발생확률은 같음
◦
예측할 수 없으며 임의성(Randomness)을 가짐
•
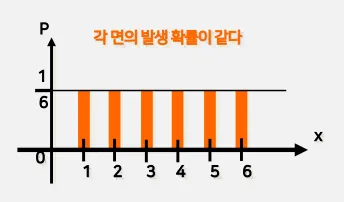
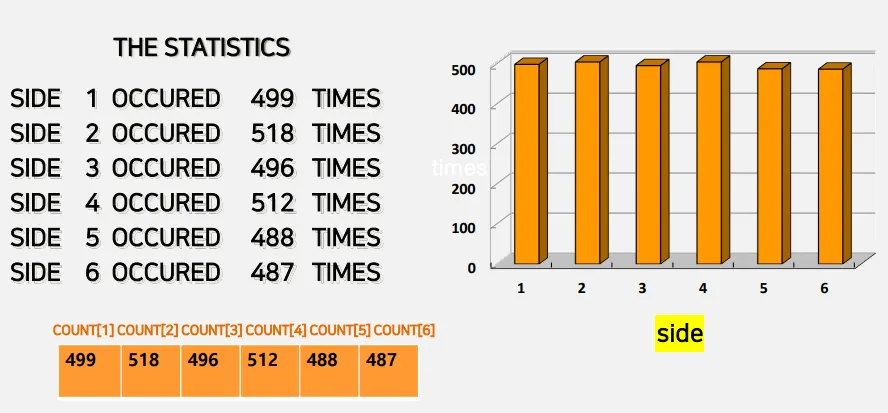
예) 주사위 던지기
◦
주사위를 충분히 많이 던지면 각 면이 나올 확률이 유사해짐
◦
그러나, 각 시도 횟수때마다 어떤 면이 나올 지를 예측할 수는 없음
3.5. 난수 발생
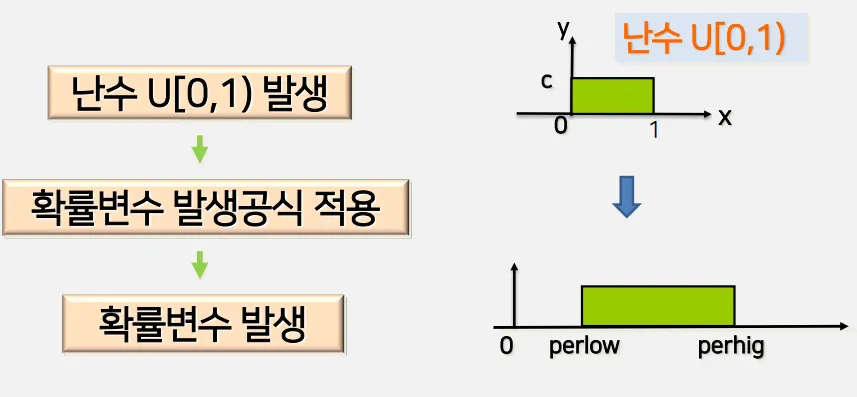
•
예) 난수 [0, 1) 발생
◦
0부터 1 범위(정확히는 1은 포함하지 않음) 구간 내에 난수가 발생
•
그 숫자들은 일양확률변수 성격을 가짐
•
원하는 공식을 적용시키면 확률 변수를 발생할 수 있음
•
난수 발생기
◦
난수를 발생시키는 프로그램
4. 확률변수의 발생
4.1. 확률변수 발생과정
•
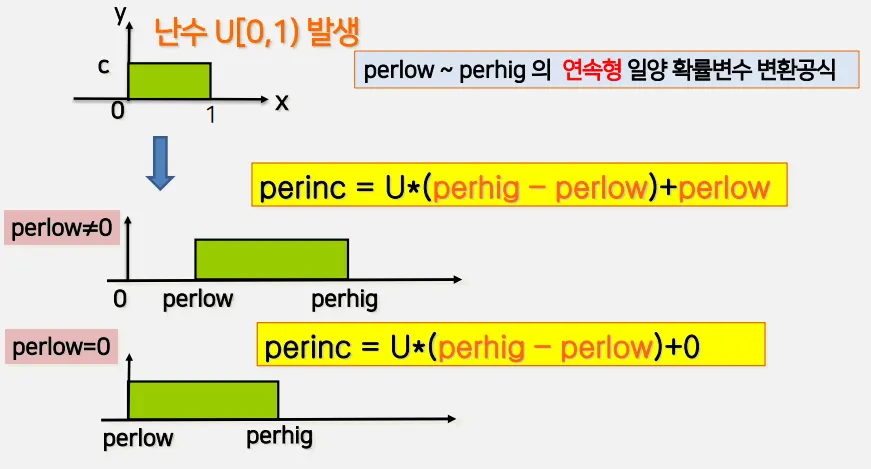
난수 U[0, 1) 발생시켜 유도 공식을 적용하여 원하는 다양한 분포의 확률 변수를 발생
•
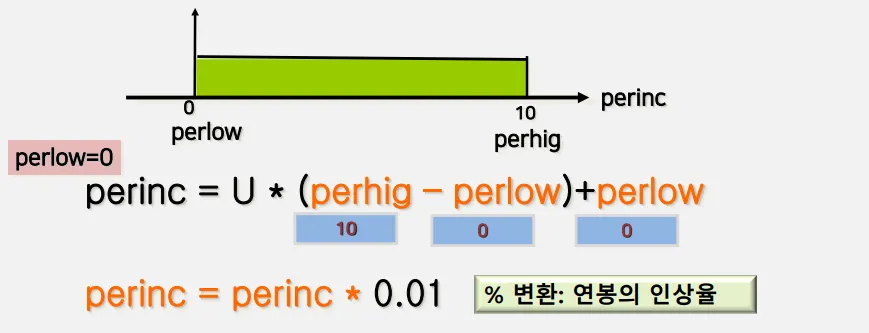
perlow ~ perhig 사이를 갖는 연속형 일양확률변수 변환공식을 이용
◦
0, 1을 각각 perlow, perhig로 변환
◦
저축문제에서는 perlow = 0, perhig가 10이됨
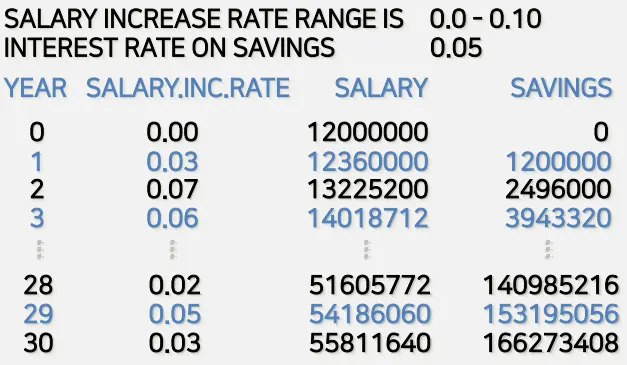
4.2. 예시 1) 저축 문제
•
배경
◦
결정적 시뮬레이션
▪
매년 연봉이 5% 상승하고, 저축액은 연봉의 10%, 은행 이율 5%로 복리 계산
▪
그러나 실제 상황은 연봉인상률, 은행 이율등이 임의적임
◦
가정
▪
연봉인상률이 0~10% 사이에 랜덤하게 적용
▪
오랫동안 관찰하면 0~10 사이가 골고루 분포 → 연속적 일양 분포
◦
연봉의 변화
▪
정확히 정수로 떨어지지 않으므로 (소수점)
▪
0~10%의 연속형 일양 확률 변수 → 0~10% 이산형 일양 확률 변수라고 가정
•
연봉 인상율 적용 → 인상율 (perinc)에 0.01 곱셈
•
이산형 일양 확률 변수
◦
0부터 10까지 정수형을 확률변수로 만들어주는 공식
•
알고리즘
◦
seed: 초기값
◦
U: 난수 - U[0, 1)
•
실행 결과
4.2. 예시 2) 주사위 문제
•
0≤ U < 1 → 난수 U[0, 1) 발생
•
call random(seed, U)
•
side = int(U * 6) + 1
•
주사위 문제 알고리즘
•
실행 결과
5. 확률변수 발생공식
•
연속형 일양 분포
•
지수 분포
•
정규 분포
•
이산형 일양 분포
•
포아송 분포