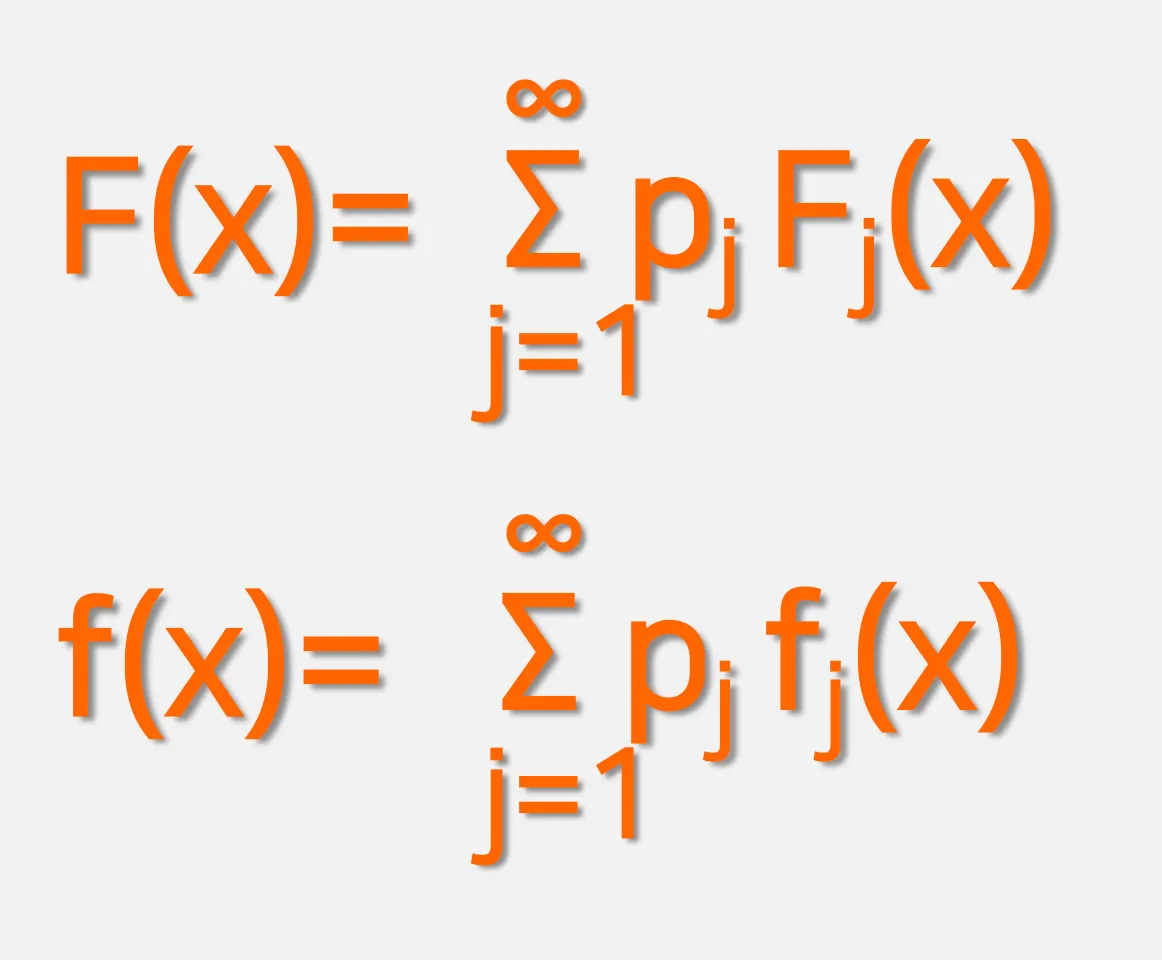Total
Search
확률변수
1. 확률변수의 기본 개념
1.1. 확률 변수 X
•
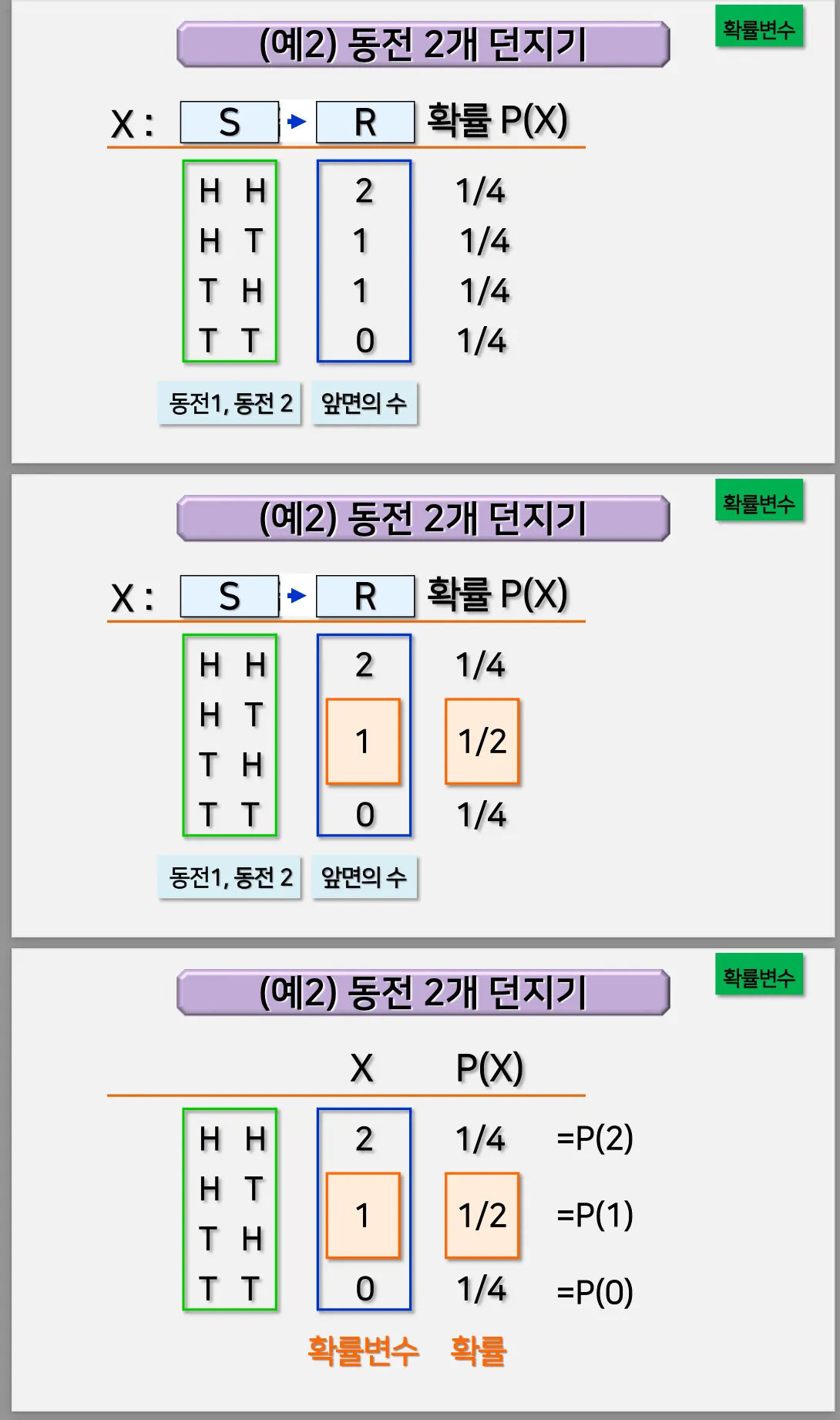
함수 X: S → R
◦
S: 표본 공간
◦
R: 실수
◦
X: 연속형 or 이산형
•
동전 1개 던지기 예시
1.2. 동전 2개 던지기 예시
2. 확률변수의 발생방법
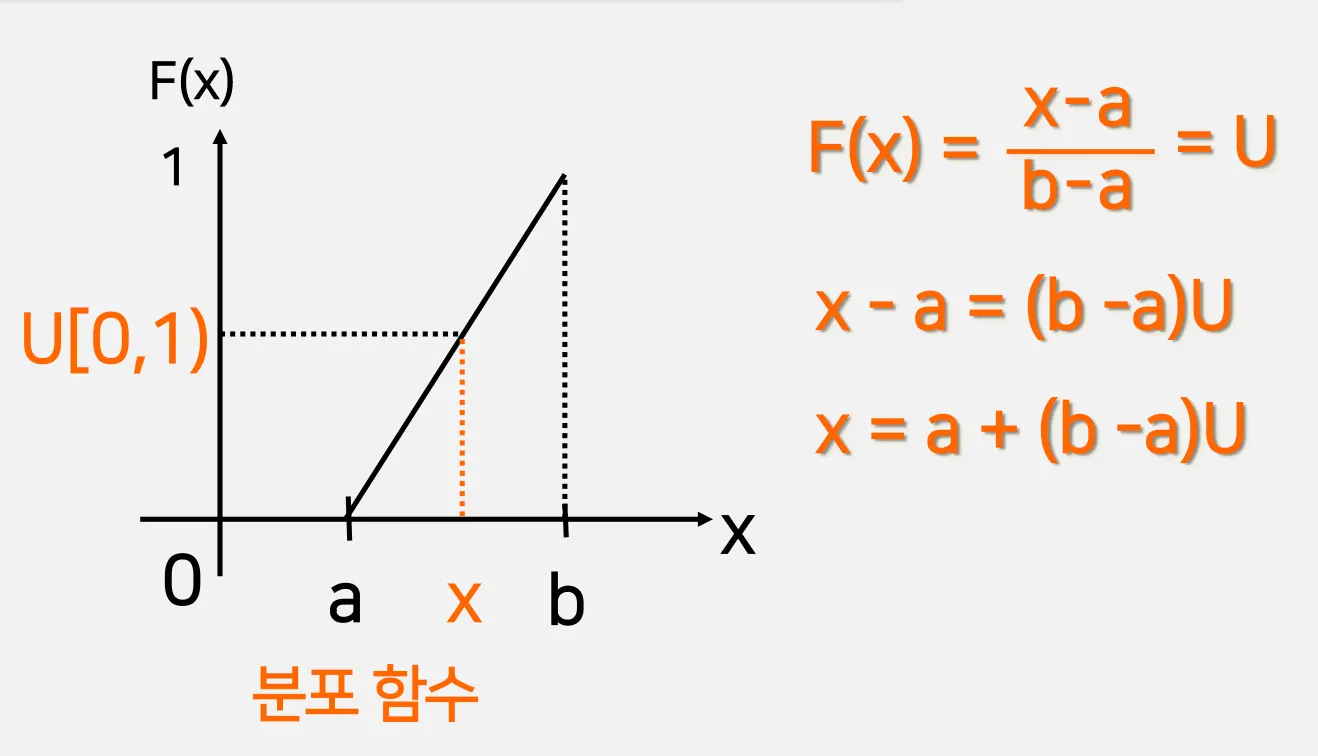
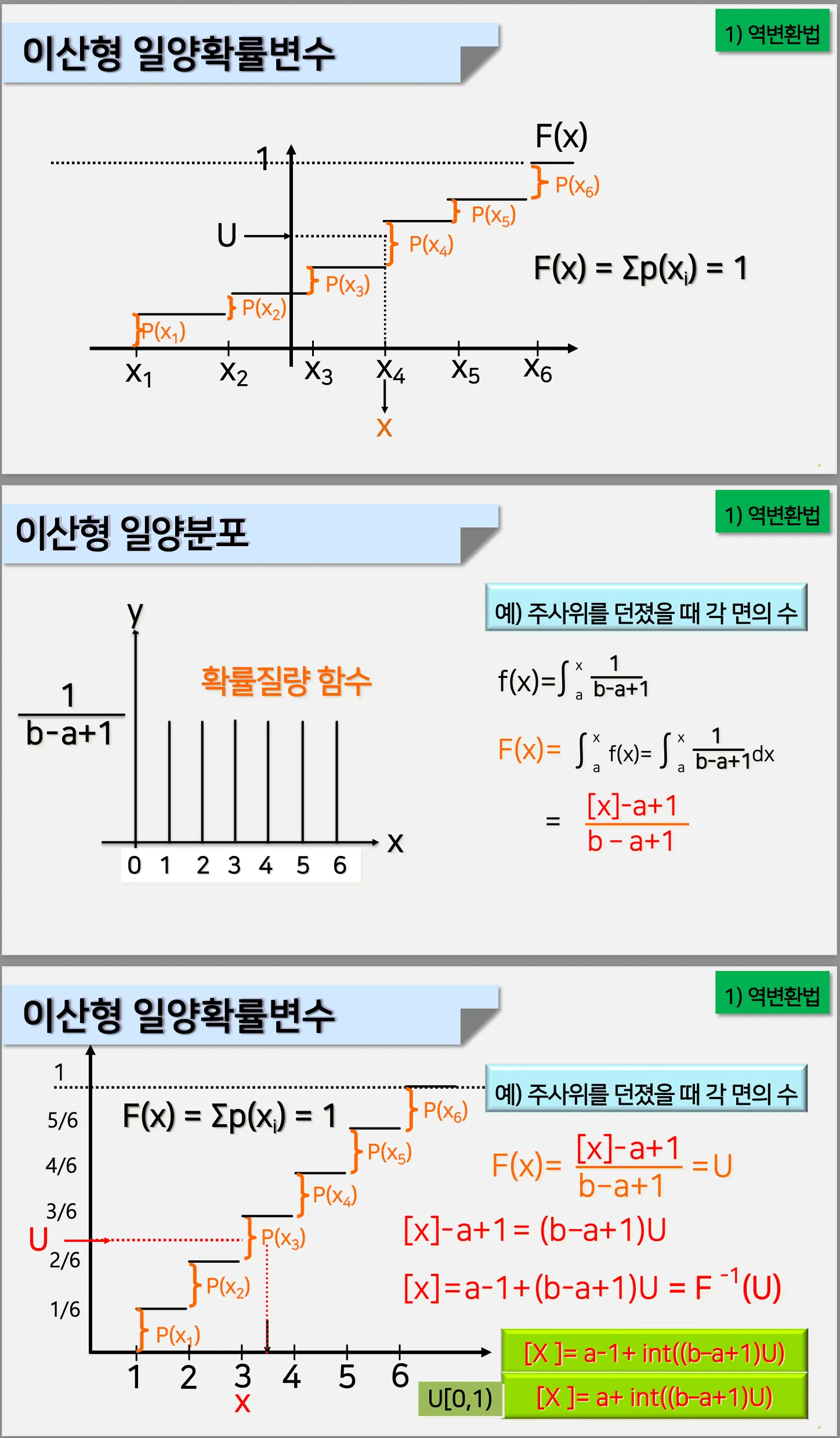
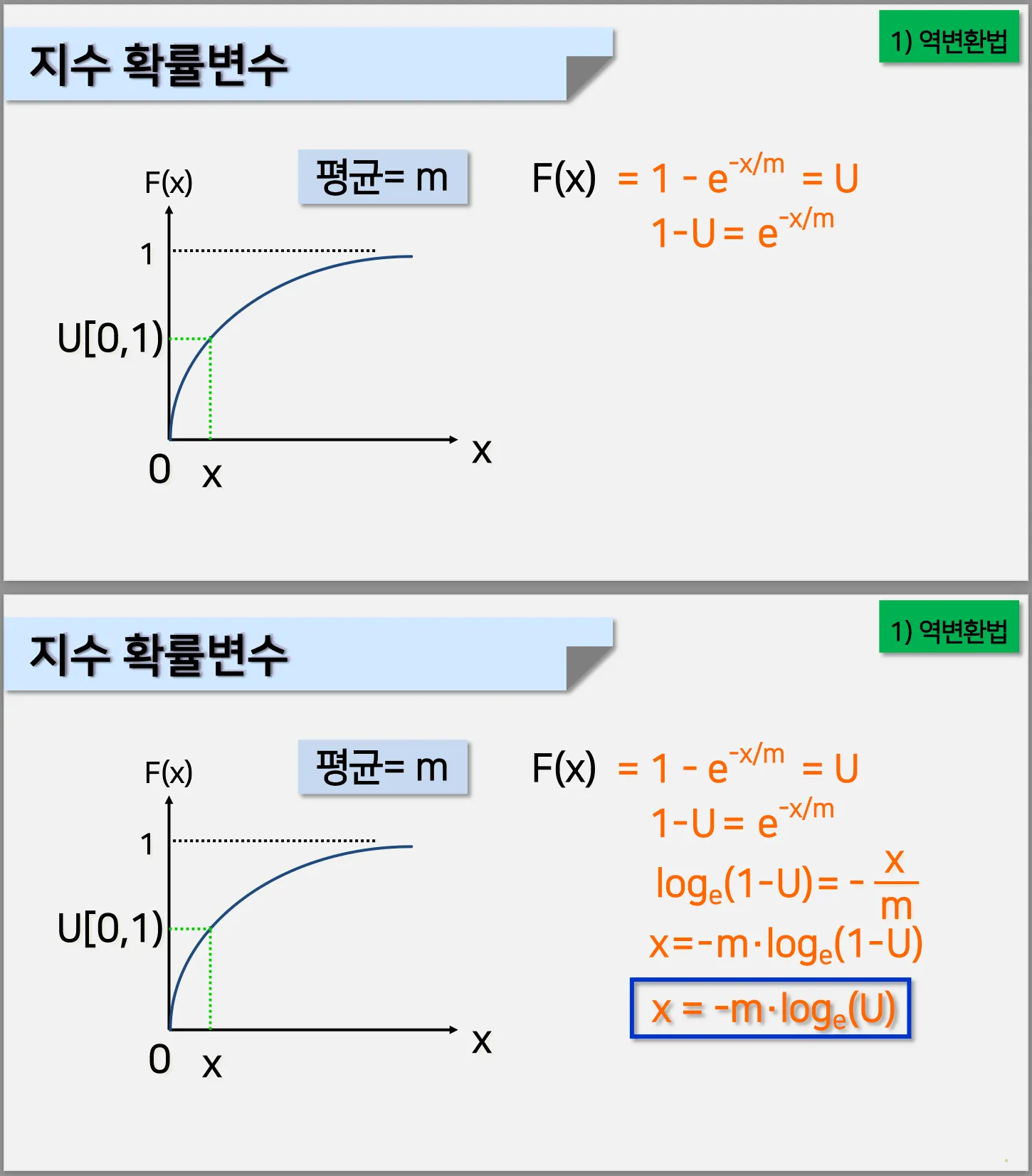
2.1. 역변환법
•
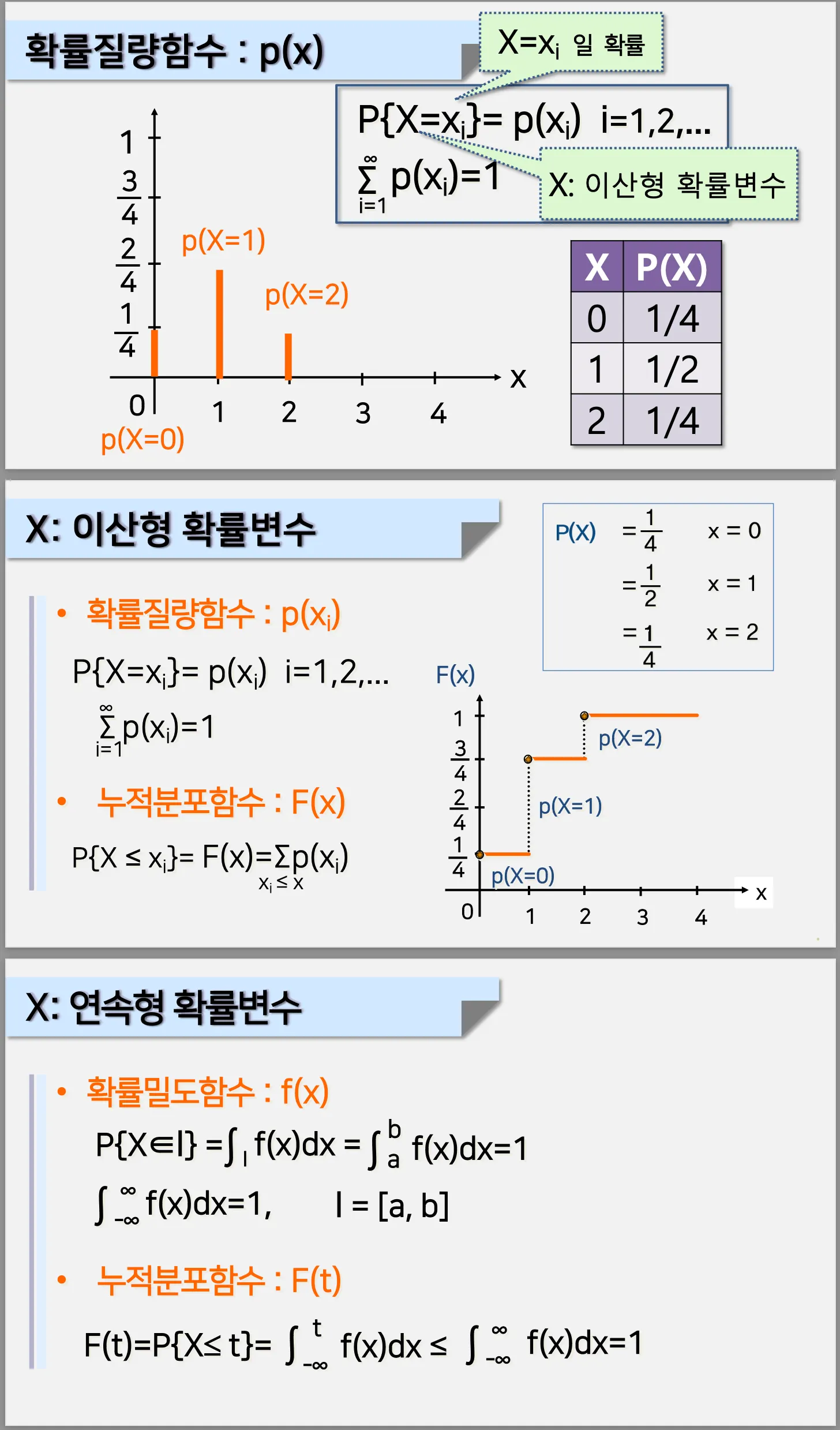
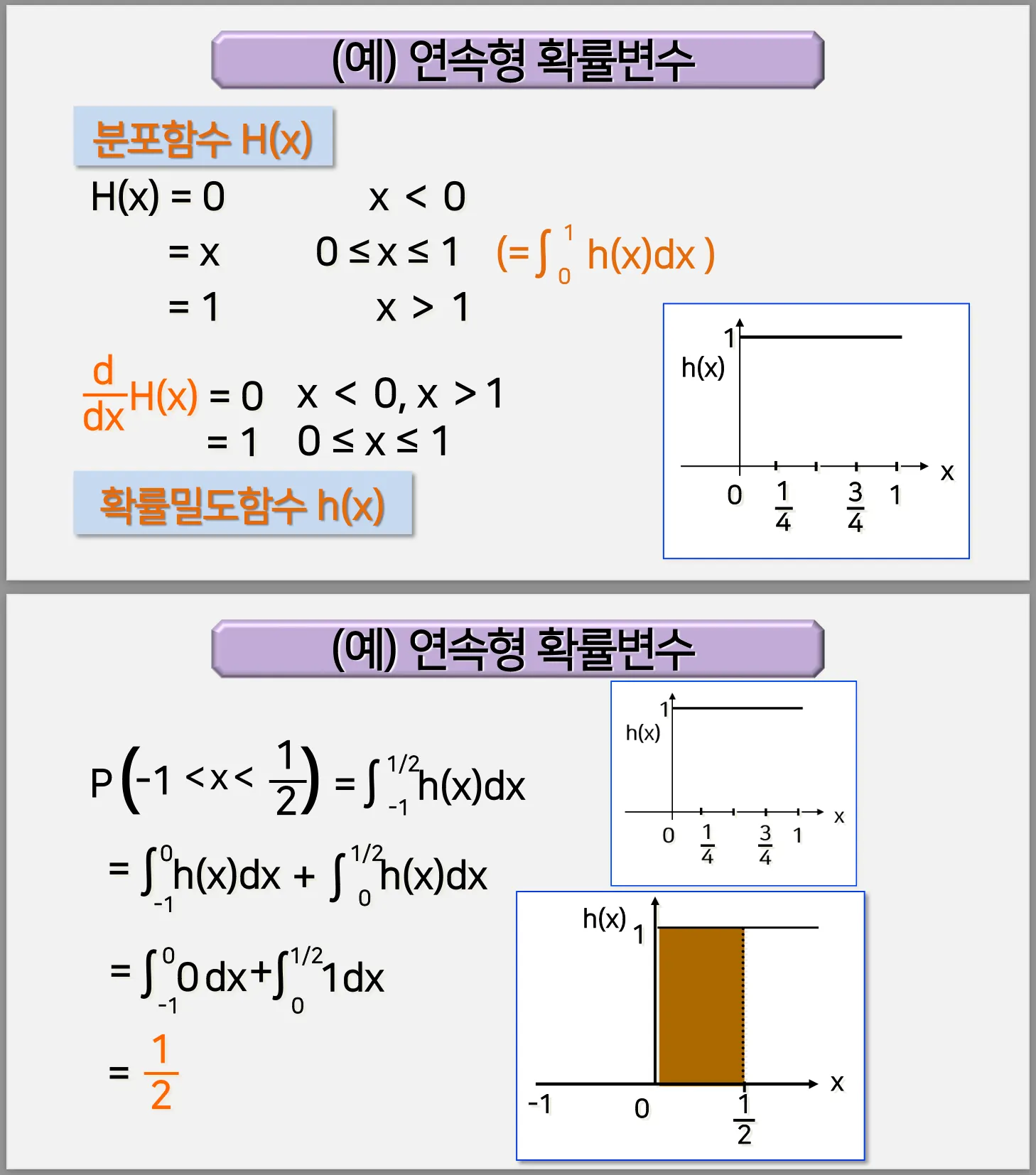
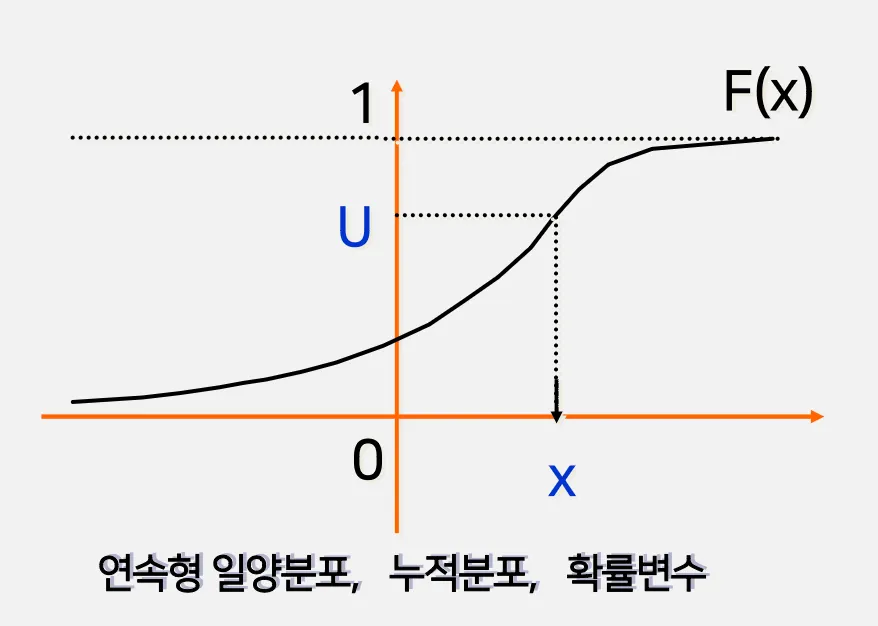
확률변수가 연속형일떄 누적분포 함수의 일반적인 형태
◦
0과 1사이의 난수 U를 구해서 그거와 매칭되는 X를 구하는 것
◦
F(x)의 역함수를 구하는 것
•
연속형 일양확률변수
•
이산형 일양확률변수
•
지수 확률변수
2.2. 합성법
•
분포함수 F가 다른 분포함수 F1, F2.. 의 조합으로 이루어진다.
2.3. 결합법
•
X = Y₁ + Y₂ + ... + Yₘ 인 경우
◦
(알고리즘)
◦
(1) 확률분포 G를 갖는 Y₁, Y₂, ..., Yₘ 발생
◦
(2) X = ∑ Yᵢ (i=1부터 m까지)
•
(예) m-Erlang 확률변수 = m 개의 지수확률변수의 합
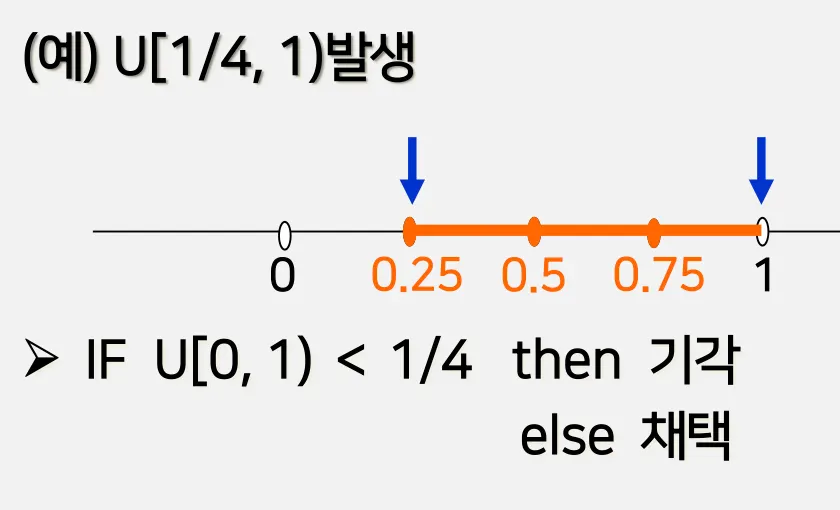
2.4. 채택기각법
1.
Uᵢ 발생
2.
IF Uᵢ ≥ 1/4 ⇒ Xᵢ = Uᵢ goto (1)
IF Uᵢ < 1/4 ⇒ goto (1)
2.5. 기타
•
정규확률변수 / 중심극한정리
•
포아송 확률변수 / 지수확률 변수와의 관계 이용
3. 확률변수의 발생공식
3.1.확률변수 발생공식
•
이론적 분포
◦
연속형 확률변수의 발생
◦
이산형 확률변수의 발생
•
경험적인 분포
◦
이론적인 분포를 구하기 어려운 경우
◦
매번 확률분포가 다르게 나온다.
◦
극한값을 구할 수 없다.
3.2. 확률변수 발생공식 선택
•
종류
◦
역변환/합성/결합/채택기각법
•
선택 기준
◦
역함수 공식이 없는 경우
◦
효율적인가?
◦
X = Y₁ + Y₂ + ... + Yₘ : m개의 Yᵢ 발생
◦
많은 Uᵢ 기각