Total
Search
난수의 발생
1. 난수 발생 알고리즘
1.1. 예제
•
알고리즘
Subprogram random(n,U)
{ n = n * 843314861 + 453816693
if (n < 0) then
{ n = n + 2147483647 + 1 }
U = n * 0.4656612E-9 }
Bash
복사
•
실행 결과
2. 난수의 성질과 발생법
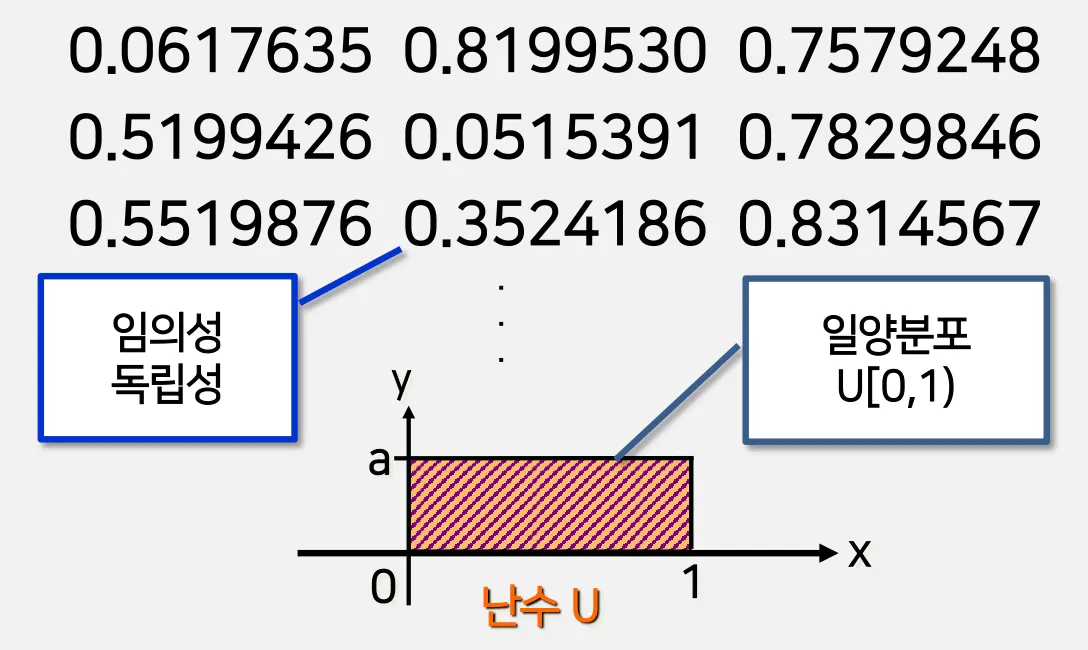
2.1. 난수의 성질
•
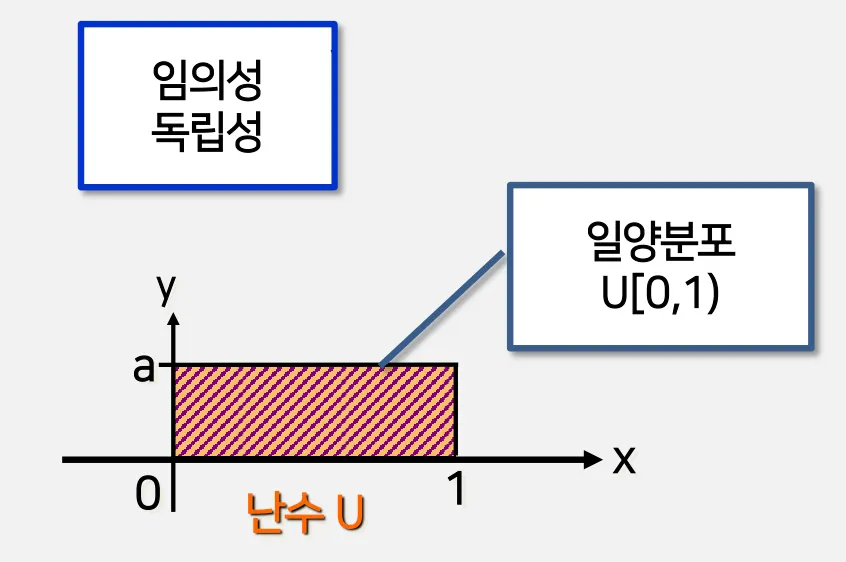
U[0,1) 일양분포
•
임의성(random)
•
상관관계가 없음
•
반복가능
•
기억용량, 발생속도
2.2. 중앙 이승법
•
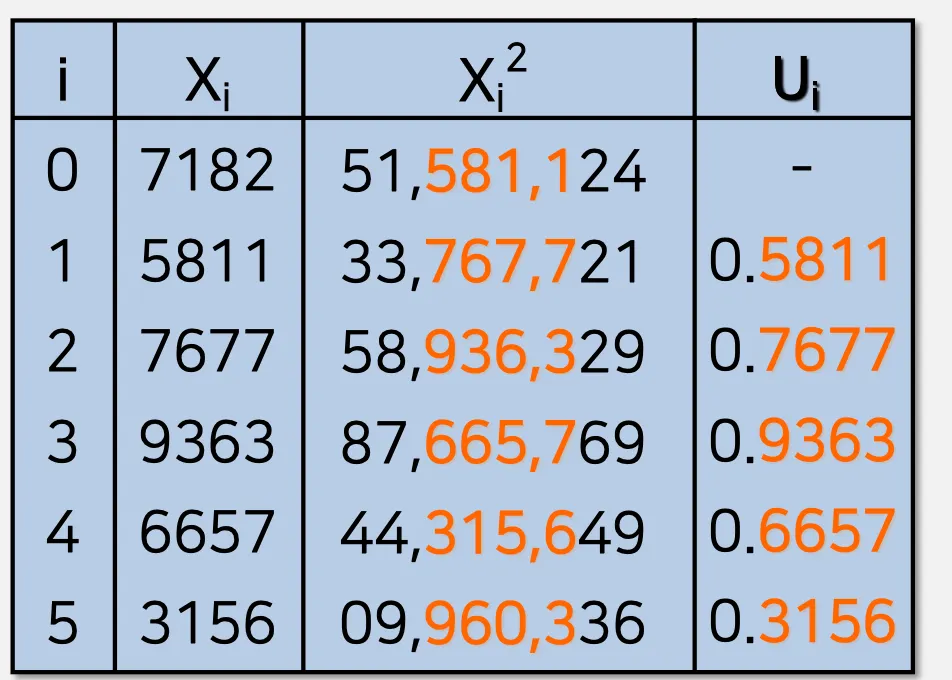
가운데 값을 활용하여 난수를 생성하는 것
•
예시)
◦
X0 = 7182
◦
X0^2 = 51,581,124
◦
X1 = 5811
◦
U1 = 0.5811
2.3. 중앙 이승법의 문제점
•
예측 가능
◦
대수적 방법
•
0으로 수렴하는 경우 중앙 이승법을 사용하기 어려움
2.4. 합동법: Lehmer의 공식
•
Xᵢ = aXᵢ₋₁ + c (mod m)
◦
a: 곱수 0 < a < m
◦
c: 증분 0 ≤ c < m
◦
m: 계수 m > 0
◦
X₀: 초기값, 0 ≤ Xᵢ ≤ m-1
2.4. 합동법 최대 주기
•
Xᵢ = aXᵢ₋₁ + c (mod m)은 다음의 경우 최대 주기를 갖는다.
•
(m, c) = 1 (서로소)
◦
m과 c는 서로 공통 인수가 없어야 함
•
q | m → q | (a-1) (q: m의 소수)
◦
m을 q로 나눈다면, q는 a-1로도 나누어져야 한다.
•
4 | m → 4 | (a-1)
◦
m을 4로 나눈다면, 4는 a-1로도 나누어져야 한다.
•
예시)
3. 컴퓨터 연산과정
3.1. 컴퓨터 연산 과정
•
Xᵢ = aXᵢ₋₁ + c (mod m)
•
m = 2ᵇ을 채택
◦
2³¹ (32bit 머신)
•
컴퓨터에서 연산을 어떻게하면 효율적으로 빨리 할 수 있을지 고민
◦
overflow 연산 활용
3.2. overflow 연산
•
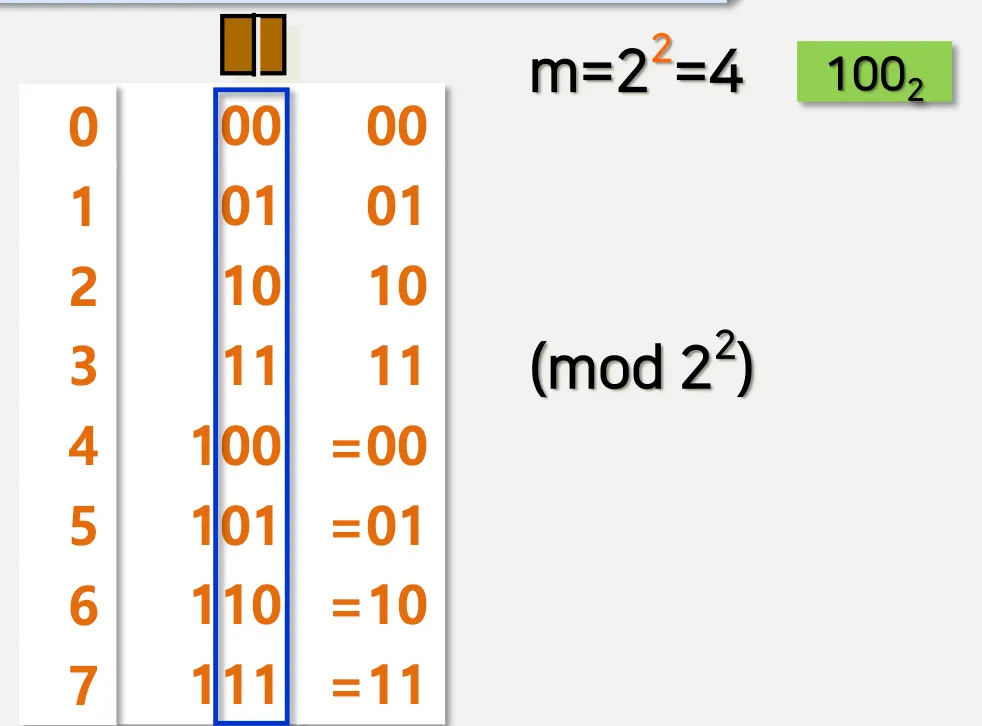
overflow 연산
◦
넘칠때 자동으로 짤리는 것이 mod와 똑같음
•
예시)
•
연산을 하지 않더라도 16을 나눴을때 오버플로우가 나머지가 됨
3.3. 컴퓨터 연산
•
컴퓨터 연산
◦
우리가 원하는 것: 2^31로 나눈 나머지
= 31개의 비트로 취한 값
= 나머지
4. 합동법
4.1. 합동법
•
혼합식 합동법 c ≠ 0 최대주기 m
◦
Xᵢ = aXᵢ₋₁ + c (mod m)
•
승산식 합동법 c = 0
◦
Xᵢ = aXᵢ₋₁ (mod m)
4.2. 승산식 합동법
•
점화식
◦
Xᵢ = aXᵢ₋₁ (mod m)
•
특징
◦
최대주기를 갖지 못함
◦
m = 2ᵇ이면 p ≤ 2ᵇ⁻²
▪
p는 주기
◦
최대주기 m-1 은 가능 (단, m 은 소수)
4.3. 합동법 문제점 Xᵢ = aXᵢ₋₁ + c (mod m)
•
Xᵢ는 결정적이다 (대수적 방법이므로)
◦
예측 가능하다.
◦
Xᵢ = [ aⁱX₀ + c(aⁱ⁻¹)/(a-1) ] (mod m)
•
Uᵢ는 유리수인 0, 1/m, 2/m, ..., (m-1)/m 값만 취한다.
◦
무리수는 표현하지 못함
•
그럼에도 의사난수, 적당한 a, c, m 선택을 선택하여 난수를 선택함
◦
m: 최대값, 검정통과
◦
Pseudo random number
난수의 검정
1. 난수의 χ² 검정 (일양분포)
•
예시)
◦
각 구간마다 30개씩 고르게 분포되어 있어야 함 (일양분포)
◦
기대값: n/ k = 30 (3000/100)
◦
실제 관측치: Oj
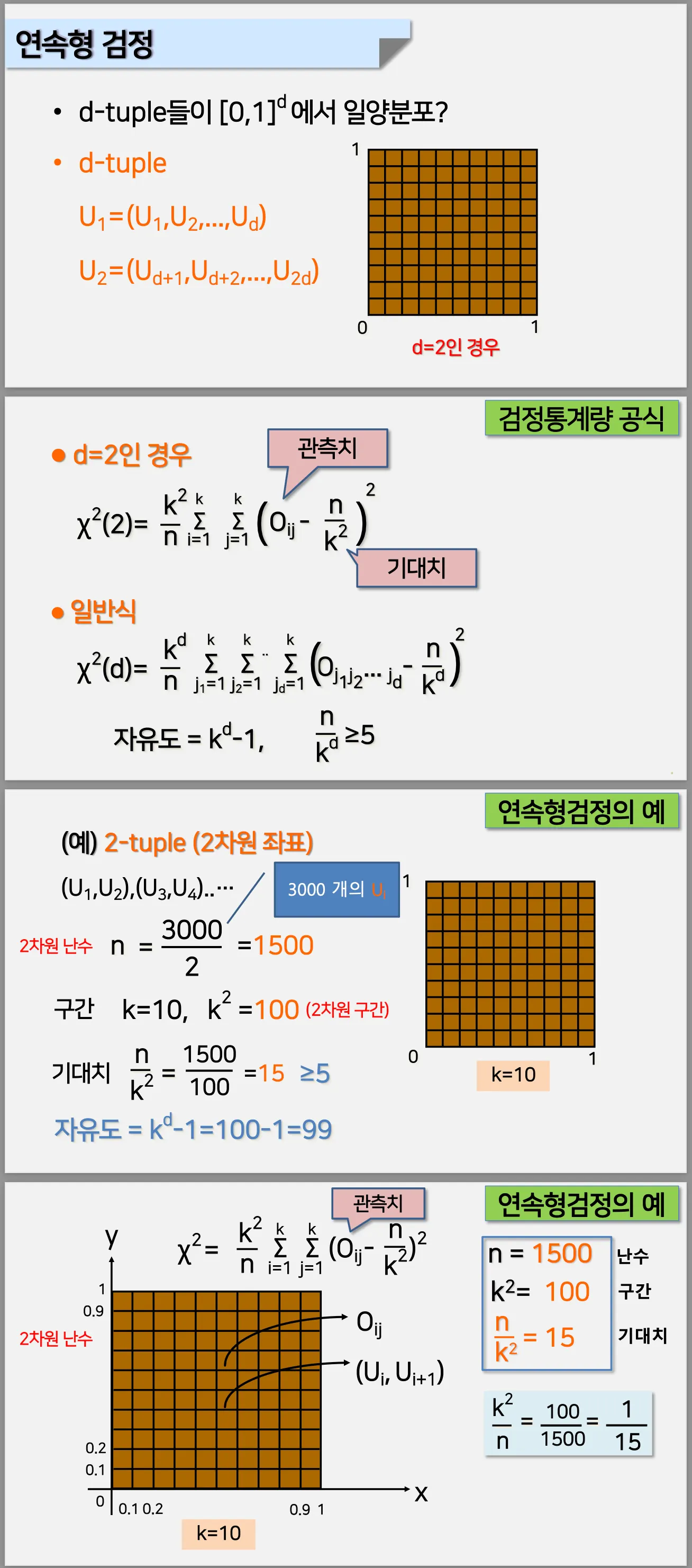
2. 연속형 검정 (d-차원)
•
2차원, 3차원 등 n 차원의 난수들에 대하여 χ² 검정을 어떻게 할 수 있을지?
3. Runs 검정 (임의성, 상관관계)
•
골고루 퍼져있더라도 난수와 난수 사이에 상관관계는 없는가?
•
독립적인가? 임의성인가?