Total
Search
1. 정렬 알고리즘 개요
1.1. 정렬
•
주어진 데이터를 값의 크기 순서에 따라 재배치하는 것
◦
오름 차순 / 내림차순
•
정렬 구분
◦
정렬 수행 시점에 데이터가 어디에 저장되어 있는가?
◦
내부 정렬
▪
정렬할 데이터를 전부 주기억장치에 올려서 정렬하는 방식
◦
외부 정렬
▪
모든 데이터를 주기억장치에 저장할 수 없는 경우, 보조기억장치에 저장해두고 그중 일부만 반복적으로 주기억장치로 옮겨와서 정렬을 수행하는 방식
1.2. 내부 정렬 알고리즘
•
정렬 방식에 따라 비교 기반 정렬 / 데이터 분포 기반 정렬로 분류
•
비교 기반 정렬
◦
값들 간의 직접적인 비교를 통해 정렬
◦
알고리즘 성능 측정 기준
▪
키값의 비교 횟수
◦
예시)
▪
선택, 버블, 삽입 정렬 O(n²)
▪
셸, 합병, 퀵, 힙 정렬 O(nlogn)
•
데이터 분포 기반 정렬
◦
데이터의 분포 정보를 활용
◦
알고리즘 성능 측정 기준
▪
데이터 이동 횟수
◦
예시)
▪
계수, 기수, 버킷 정렬 O(n)
1.3. 안정 정렬 / 제자리 정렬
•
안정적 정렬(Stable)
◦
동일한 값을 가진 데이터의 상대적 순서를 유지하는 정렬
•
제자리 정렬(In-place)
◦
추가적인 메모리를 거의 사용하지 않는 정렬 (상수 크기의 추가 공간만 사용)
◦
입력 크기 n이 증가하더라도 추가적인 저장 공간은 증가하지 않음
1.4. 정렬 알고리즘의 기본 가정
•
입력 크기: 0 ~ n-1 개까지 총 n개
•
입력 데이터: 양의 정수
•
정렬 방식: 오름 차순
2. 선택 정렬 (Selection Sort)
2.1. 개념
•
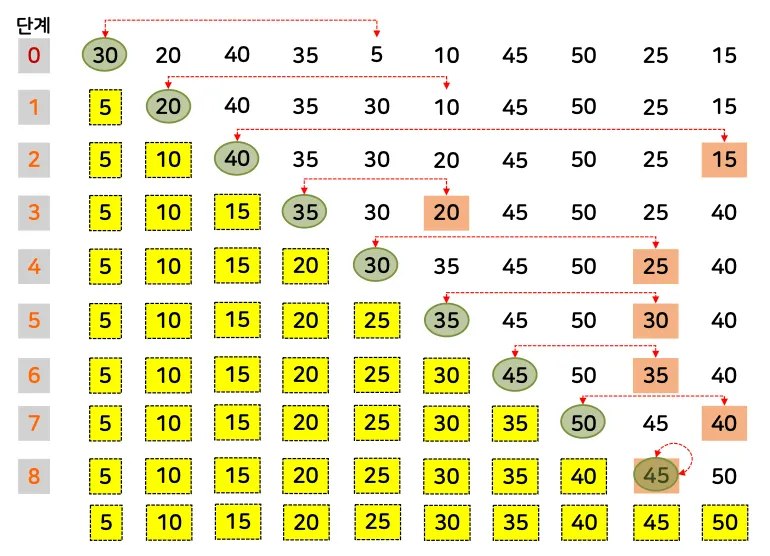
가장 작은 값부터 선택하여 맨 앞쪽에 위치시키는 정렬 방식
•
미정렬 부분에서 최솟값을 찾고, 해당 최솟값을 미정렬 부분의 첫 번째 위치와 교환하는 과정을 반복
•
예시)
2.2. 특징
•
시간 복잡도: O(n²)
•
안정성: 불안정적
•
제자리 정렬: O(1) 추가 공간 사용
◦
i, j, min,m tmp 등의 상수만 필요
•
입력 데이터 순서에 민감하지 않아, 항상 동일한 O(n²) 성능
2.3. 예시 코드
SelectionSort(A[], n) {
// (n-1)번 반복
for (i = 0; i < n-1; i++) {
min = i;
// A[i..n-1]에서 최소값 찾기
for (j = i+1; j < n; j++) {
if (A[min] > A[j])
min = j;
}
// 최소값과 A[i]의 위치 교환
Swap(A[i], A[min]);
}
return (A);
}
C
복사
def selection_sort(A):
n = len(A)
for i in range(n - 1):
min_index = i
for j in range(i+1, n):
if A[min_index] > A[j]:
min_index = j
A[i], A[min_index] = A[min_index], A[i]
return A
Python
복사
3. 버블 정렬 (Bubble Sort)
3.1. 개념
•
인접한 두 데이터를 비교하며 정렬을 수행
•
왼쪽에서 오른쪽으로 진행하며, 더 큰 데이터를 오른쪽으로 이동시키는 과정을 반복
•
예시)
3.2. 특징
•
시간 복잡도: O(n²)
•
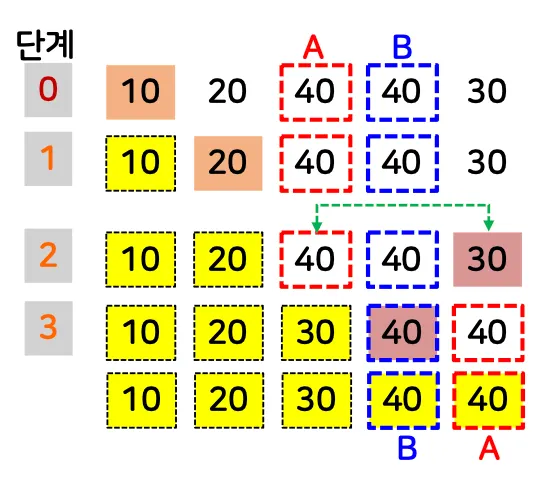
안정성: 안정적
◦
인접한 두 데이터가 동일한 경우 → 위치 교환 X
•
제자리 정렬: O(1) 추가 공간 사용
•
개선 가능
◦
이미 정렬된 상태라면 O(n), 역순이면 O(n²)
•
선택 정렬에 비해 데이터 교환 횟수가 많음
◦
선택 정렬보다 비효율적
3.3. 개선된 버블 정렬 알고리즘
•
각 루프의 반복 횟수를 줄여서 개선 가능
◦
처리단계의 수
▪
자리 바꿈이 발생하지 않으면 이미 정렬된 상태임
▪
이후 처리 단계를 수행하지 않고 종료
◦
인접한 두 데이터 비교 횟수
▪
각 단계에서 무조건 오른쪽/왼쪽 끝까지 이동하면서 인접한 두 데이터의 비교가 불필요
→ 이미 제자리를 잡은 데이터에 대해서는 비교를 수행하지 않음
•
입력된 데이터의 상태에 따라 성능이 달라질 수 있음
◦
O(n) ~ O(n²)
3.4. 예시 코드
BubbleSort(A[], n) {
for (i = 0; i < n-1; i++) { // 단계: (n-1)번 반복
for (j = 0; j < n-1; j++) { // 왼쪽에서 오른쪽으로 진행
if (A[j] > A[j+1]) {
// '왼쪽 데이터 > 오른쪽 데이터'이면 자리바꿈
Swap(A[j], A[j+1]);
}
}
}
return (A);
}
Advanced_BubbleSort(A[], n) {
for (i = 0; i < n-1; i++) { // 단계: 0, 1, ..., (n-2)
Sorted = TRUE; // 이미 정렬되었다고 가정
for (j = 0; j < (n-1)-i; j++) { // 왼쪽에서 오른쪽으로 진행
if (A[j] > A[j+1]) {
// 왼쪽 데이터 > 오른쪽 데이터이면 교환
Swap(A[j], A[j+1]);
Sorted = FALSE; // 자리바꿈 발생 → 미정렬 상태
}
}
if (Sorted == TRUE) break; // 이미 정렬된 상태라면 종료
}
return (A);
}
C
복사
def bubble_sort(A):
n = len(A)
for i in range(n - 1): # (n-1)단계 반복
for j in range(n - 1): # 각 단계마다 왼쪽에서 오른쪽으로 진행
if A[j] > A[j + 1]:
# 왼쪽 데이터가 오른쪽 데이터보다 크면 교환
A[j], A[j + 1] = A[j + 1], A[j]
return A
def advanced_bubble_sort(A):
n = len(A)
for i in range(n - 1): # 단계: 0, 1, ..., (n-2)
sorted_flag = True # 이미 정렬되었다고 가정
for j in range(n - 1 - i): # 각 단계마다 비교 범위 축소
if A[j] > A[j + 1]:
A[j], A[j + 1] = A[j + 1], A[j] # 자리바꿈
sorted_flag = False # 자리바꿈 발생 → 미정렬 상태
if sorted_flag: # 자리바꿈이 없었다면 이미 정렬 완료
break
return A
Python
복사
4. 삽입 정렬(Insertion Sort)
4.1. 개념
•
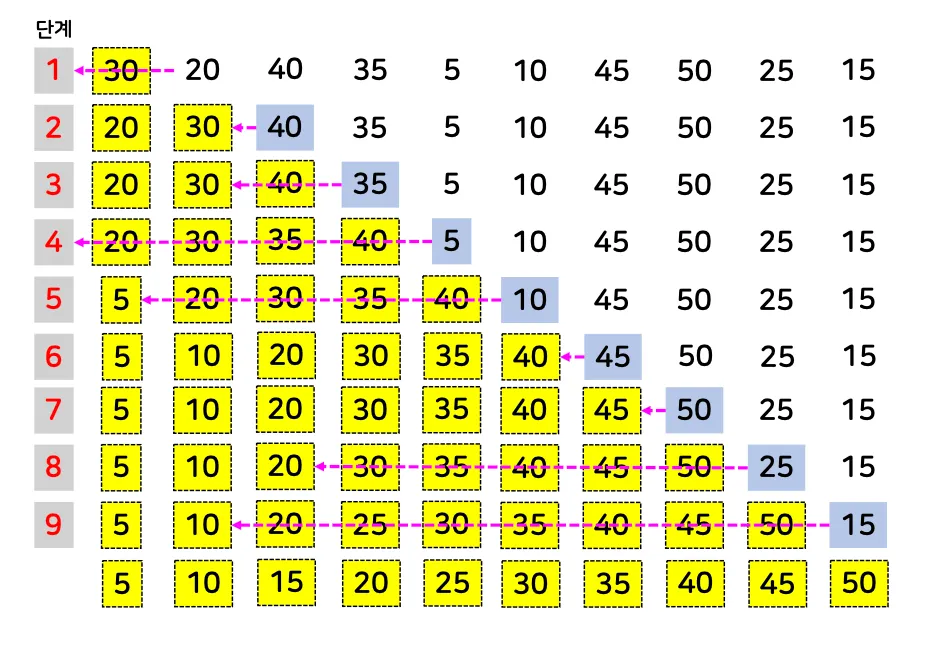
주어진 데이터를 하나씩 뽑은 후 이미 나열된 데이터가 항상 정렬된 상태를 유지하도록 뽑은 데이터를 바른 위치에 삽입해서 나열하는 방식
•
항상 정렬된 상태를 유지하도록 새로운 데이터를 알맞은 위치에 삽입
•
예시)
4.2. 특징
•
시간 복잡도: 평균 O(n²), 최선 O(n) (거의 정렬되어 있을 때)
•
안정성: 안정적
◦
인접한 두 데이터가 정렬되지 않은 경우에만 위치 교환 발생
•
제자리 정렬: O(1)
•
데이터 순서에 민감 → 역순 정렬 시 O(n²)
4.3. 예시 코드
InsertionSort(A[], n) {
for (i = 1; i < n; i++) { // A[0]은 이미 정렬된 상태로 가정
val = A[i]; // 미정렬 부분 A[i..n-1]에서 첫 번째 데이터 선택
j = i;
// 삽입 위치 찾기
while (j > 0 && A[j - 1] > val) {
A[j] = A[j - 1]; // 정렬된 부분의 원소가 더 크면, 한 칸 뒤로 이동
j--;
}
A[j] = val; // 찾은 삽입 위치에 val 삽입
}
return (A);
}
C
복사
def insertion_sort(A):
n = len(A)
for i in range(1, n): # A[0]은 이미 정렬된 상태로 가정
val = A[i] # 미정렬 부분 A[i..n-1]에서 첫 번째 데이터 선택
j = i
# 삽입 위치 찾기
while j > 0 and A[j - 1] > val:
A[j] = A[j - 1] # 정렬된 부분의 원소가 더 크면, 한 칸 뒤로 이동
j -= 1
A[j] = val # 찾은 삽입 위치에 val 삽입
return A
Python
복사
5. 셸 정렬(Shell Sort)
5.1. 개념
•
삽입 정렬의 개선 버전
◦
삽입 정렬의 단점: 현재 삽입하고자 하는 데이터가 삽입될 제 위치에서 많이 벗어나 있어도 한번에 한 자리씩만 이동해서 찾아가야함
•
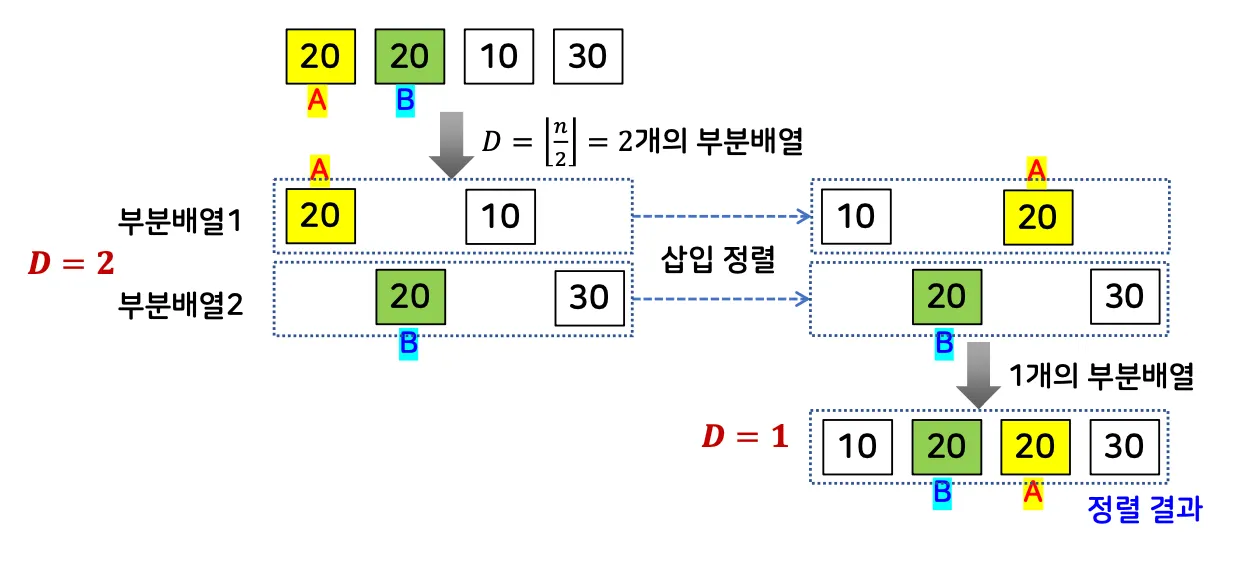
먼 거리에 있는 원소들을 먼저 정렬한 뒤, 점차 간격을 줄여가며 정렬 수행
•
압력 배열을 부분 배열로 나누어 삽입정렬을 수행하는 과정을 부분 배열의 크기와 개수를 변화시켜 가면서 반복
5.2. 특징
•
시간 복잡도: 평균적으로 O(n^(3/2)) ~ O(n^(5/4)) 등, 일반적으로 O(n²) 이하로 개선 가능, 하지만 단순 구현 시 O(n²)로 보기도 함
•
안정성: 불안정적
•
제자리 정렬: O(1) 추가 공간 사용
•
사용되는 '순열(간격)'에 따라 성능 차이 발생
◦
가장 좋은 간격을 찾는 것은 아직 미해결 과제
5.3. 예시 코드
•
비고
◦
하나의 입력 배열을 물리적으로 여러 개의 부분 배열로 분할하지 않음
◦
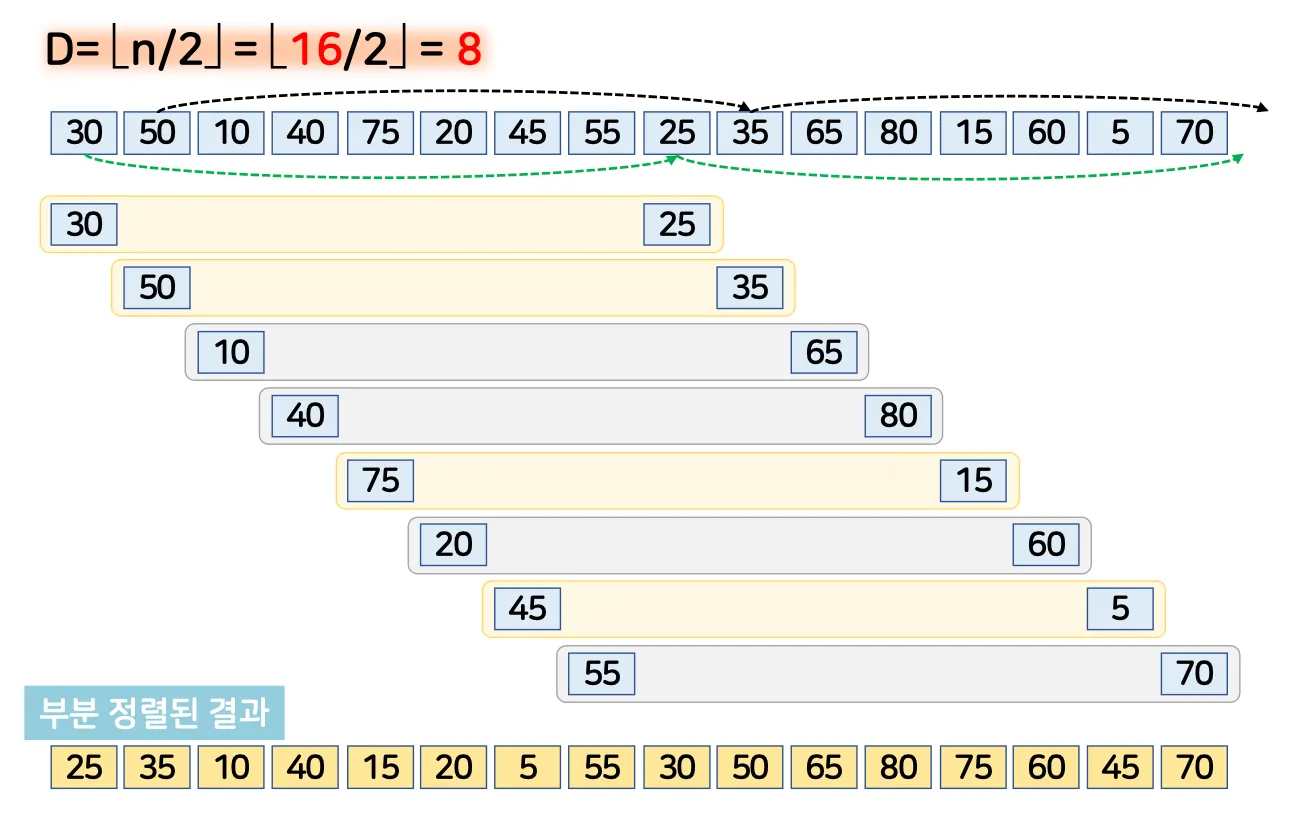
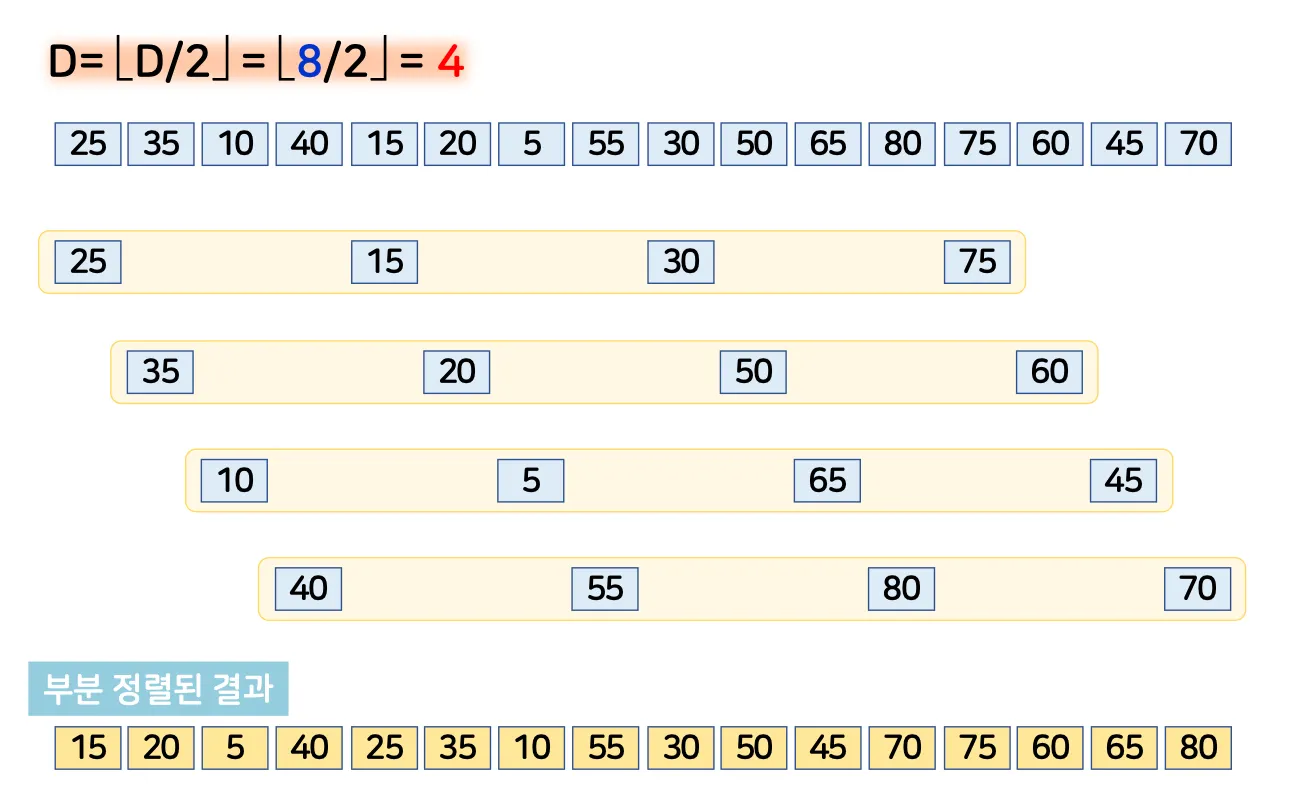
각 부분배열을 번갈아 가면서 미정렬 부분의 첫번째 데이터를 뽑은 후 D 만큼 떨어진 정렬 부분에서 제자리를 찾아서 삽입하는 방식
•
변수 D
◦
부분 배열의 갯수
◦
각 부분배열 내에서 이웃한 데이터간의 거리
ShellSort(A[], n) {
// D: 부분배열(간격) 크기 설정
for (D = n / 2; D >= 1; D = D / 2) {
for (i = D; i < n; i++) {
val = A[i];
j = i;
// 삽입할 위치를 찾으며, 간격 D만큼 떨어진 요소들과 비교
while (j >= D && A[j - D] > val) {
A[j] = A[j - D];
j = j - D;
}
A[j] = val;
}
}
return (A);
}
C
복사
def shell_sort(A):
n = len(A)
D = n // 2 # 초기 간격 설정
while D >= 1:
for i in range(D, n):
val = A[i]
j = i
# 간격 D만큼 떨어진 원소들과 비교하며 삽입할 위치 찾기
while j >= D and A[j - D] > val:
A[j] = A[j - D]
j -= D
A[j] = val
D //= 2 # 간격을 줄여가며 반복
return A
Python
복사