Total
Search
1. 스트링 알고리즘 관련 기본 개념
•
스트링(String)
◦
문자가 연속적으로 나열된 문자열
•
알파벳 ∑
◦
스트링에 사용되는 문자들의 집합
•
스트링 알고리즘
◦
스트링에 대한 다양한 문제를 해결하는 알고리즘 통칭
◦
예) 스트링 매칭, 스트링 압축, 최장 공통 부분 수열 등
•
스트링 매칭
◦
텍스트에서 패턴이 나타나는 위치를 찾는 문제
2. 브루트-포스 스트링 매칭 알고리즘
2.1. 개념
•
텍스트의 각 위치에서부터 패턴의 길이만큼 문자를 비교하며 매치를 찾음
2.2. 알고리즘
•
성능 O(nm)
BruteForce(n, T[], m, P[])
{
for (i = 0; i <= n - m; i++) { // 텍스트의 가능한 모든 위치에서 O(n)
flag = true;
for (j = 0; j < m; j++) { // 패턴의 길이만큼 O(m)
if (T[i + j] != P[j]) { // 텍스트와 패턴의 문자를 비교
flag = false; // 일치하지 않으면 플래그를 false로 설정
break;
}
}
if (flag) 위치 i 출력; // 플래그가 true면 매치 위치 출력
}
}
C
복사
2.3. 스트링 매칭 알고리즘 고도화
•
패턴 전처리
◦
라빈-카프 알고리즘
◦
KMP 알고리즘
◦
보이어-무어 알고리즘
•
텍스트 전처리
◦
접미부 트리
◦
접미부 배열
3. 라빈-카프 알고리즘 (Rabin-Karp)
3.1. 개념
•
방법
◦
패턴의 해시값을 먼저 계산
◦
패턴의 해시값으로 매치의 후보를 찾음
◦
후보에 대해서만 문자별로 비교하여 매치를 확인
◦
텍스트의 각 위치마다 해시값 계산이 필요하지만, 직전 위치의 해시값을 이용하여 상수 시간에 계산 가능
•
해시 함수
◦
문자열을 위한 가중합 활용
◦
예시)
▪
a~z: 총 26개
▪
패턴의 길이: 5 → 해시 함수의 지수 값이 4부터 시작
•
위와 같은 방식은 모든 경우의 수를 해시값 후보를 찾아서 비교하므로 브루트 포스 스트링 비교 알고리즘과 크게 다르지 않음 → 고도화
3.2. 텍스트 위치별 해시값 계산
•
위치 0: O(m)
•
위치 1~n-m: O(1)
◦
해시 함수의 특징을 이용
◦
직전에 계산했던 해시 값을 활용
▪
지수 값을 1씩 더 증가
▪
누락되는 값은 제거: 0 x 26^5
3.3. 알고리즘
RabinKarp(n, T[], m, P[])
{
int hp = 0, ht = 0; // 패턴과 텍스트의 초기 해시값
int dm = pow(26, m) % M; // 패턴 길이에 따른 상수값 계산
// 초기 해시값 계산 (패턴과 텍스트의 첫 부분)
for (j = 0; j < m; j++) {
hp = (hp * 26 + P[j] - 97) % M; // 패턴의 해시값
ht = (ht * 26 + T[j] - 97) % M; // 텍스트의 위치 0 해시값
}
// 텍스트의 가능한 모든 위치에서 해시값 비교
for (i = 0; i <= n - m; i++) {
// 현재 해시값이 일치하는 경우
if (hp == ht) {
flag = true;
for (j = 0; j < m; j++) { // 패턴의 길이만큼 문자 비교
if (T[i + j] != P[j]) {
flag = false;
break;
}
}
if (flag) 위치 i 출력; // 일치하는 위치 출력
}
// 다음 위치의 해시값 계산
if (i < n - m) {
ht = (ht * 26 - dm * (T[i] - 97) + (T[i + m] - 97)) % M;
if (ht < 0) ht += M; // 음수 값 방지
}
}
}
C
복사
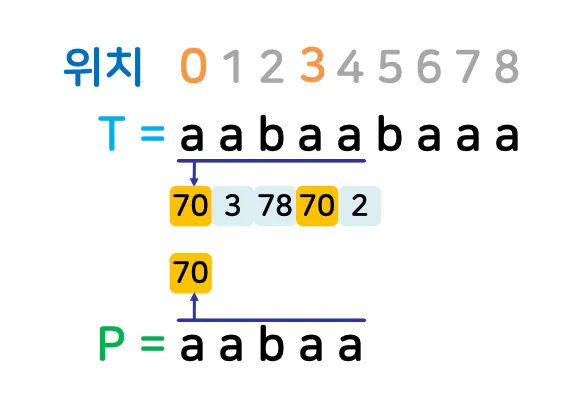
3.4. 예시
•
텍스트 T=10011100에서 패턴 P=0011이 매치되는 모든 위치?
◦
1번째 위치 h(1001) 해시 값 9, 패턴의 해시 값과 일치 X → 매칭 X
◦
2번째 위치 h(0011) 해시 값 계산 시 직전 계산 값 활용
▪
이전 해시값 9에 2를 곱함
▪
직전 위치에서 사라지는 문자열 1을 빼줌 -1 x 2^4
▪
새롭게 추가되는 문자열에 대하여 계산
◦
마찬가지로 반복
3.5. 성능과 특징
•
성능 → O(n+km)
◦
전처리 → O(m)
▪
m은 패턴의 길이
◦
텍스트에서 해시값 계산 → O(n)
▪
n은 텍스트의 길이
◦
후보 위치는 문자 직접 비교. 매치 후보의 개수 k → O(km)
•
최선의 시간 복잡도 O(n)
◦
매치 개수가 상수
•
최악의 시간 복잡도 O(nm)
◦
모든 위치에서 매치
4. KMP 알고리즘 (Knuth-Morris-Pratt)
4.1. 개념
•
패턴 내 문자 관계를 이용하여 중복된 비교를 줄임
•
텍스트의 첫 위치에서 패턴의 앞부분부터 문자 비교
•
불일치 발생 시
◦
이미 일치한 서브스트링 정보를 활용
◦
접두부와 접미부의 최대 일치 정보를 이용해 다음 위치로 이동
4.2. 일치한 서브스트링에 대한 접두부와 접미부의 최대 일치 정보
•
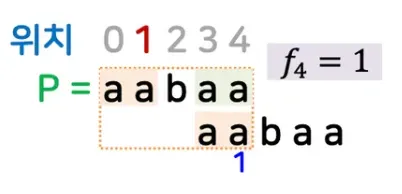
첫번째 케이스
◦
패턴의 제일 마지막 위치: 4
◦
접두부와 접미부의 최대 일치 정보?
▪
접두부 aa, 접미부 aa
◦
접두부의 제일 마지막 위치는? 1
◦
위치 4에서 접두부의 제일 마지막 위치인 1을 저장하자 → f4 = 1
◦
이용 방법?
▪
매치 할때, f4라는 곳에 일치가 발생하면, 패턴의 위치를 f4 라는 값만큼 이동
▪
f4라는 값을 1이라고 했으니, 패턴의 위치인 1이 현재 4위치 하도록 이동
•
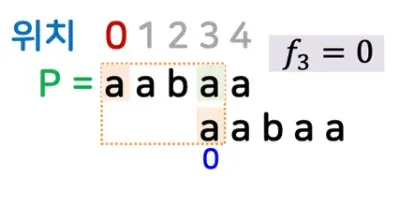
두번째 케이스
◦
접두부와 접미부 최대 일치 정보
▪
접두부 a, 접미부 a
◦
마지막 위치 3: f3
◦
접두부의 마지막 위치: 0
→ f3 = 0
•
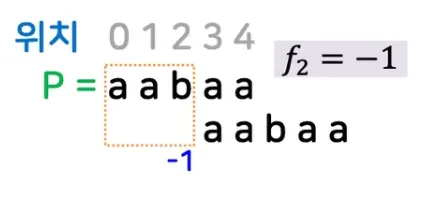
세번째 케이스
◦
접두부와 접미부의 최대 일치가 없는 경우 → -1
◦
f 값으로 저장된 값이 현재 위치로 와야함
◦
패턴의 -1을 여기에 두겠다는 것은, 매치를 건너뛰고 그다음 위치에 두겠다는 의미
•
최종 요약
4.2. 알고리즘
•
KMP 전처리 알고리즘
◦
패턴의 위치 0부터 m-1까지 차례대로 F[i], 즉 최대 일치 정보 𝑓𝑖 구함
PreKMP(m, P[])
{
// idx 변수: 직전 위치에서 찾은 f 값.
int F[m], idx = -1;
F[0] = -1;
for (i = 1; i < m; i++) {
while (idx >= 0 && P[i] != P[idx + 1])
idx = F[idx]; // 최대 접두부 찾기
if (P[i] == P[idx + 1])
idx++; // 마지막 문자 일치
F[i] = idx; // i에서의 최대 접두부 설정
}
return (F);
}
C
복사
•
KMP 알고리즘
KMP(n, T[], m, P[])
{
F[0..m-1] = PreKMP(m, P); // 패턴 전처리
int j = -1;
for (i = 0; i < n; i++) {
while (j >= 0 && T[i] != P[j + 1])
j = F[j]; // 최대 접두부로 이동
if (T[i] == P[j + 1])
j++; // 패턴 문자 일치
if (j == m - 1) { // 패턴 끝까지 일치
위치 i - j 출력; // 매칭 위치 출력
j = F[j]; // 다음 매칭을 위해 이동
}
}
}
C
복사
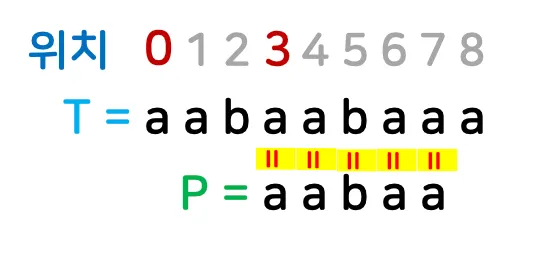
4.3. 예시
텍스트 T=aabaabaaa에서 패턴 P=aabaa가 매치되는 모든 위치?
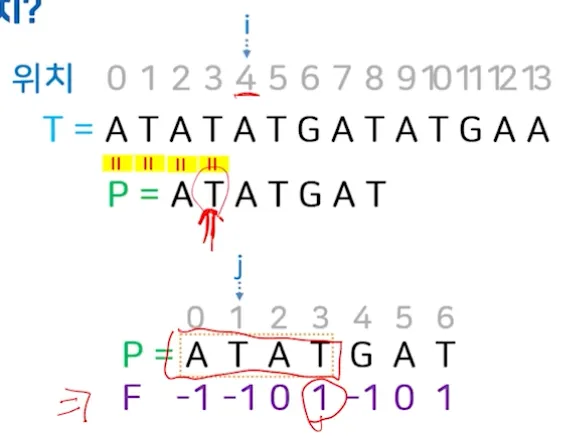
텍스트 T=ATATATGATATGAA에서 패턴 P=ATATGAT가 매치되는 모든 위치?
1.
패턴에 대하여 최대일치정보(F) 계산
2.
텍스트에 대한 위치 확인
a.
위치 0에서 일치 확인 (i=4, i는 일치하는 패턴의 길이를 의미)
i.
텍스트 4에서 불일치 확인
ii.
패턴기준으로는 ATAT 까지만 일치 ( j = 3)
iii.
이때의 접두부/접미부의 최대일치정보 f = 1
1.
최대 일치 정보인 1에 해당하는 위치로 j 이동
iv.
패턴의 위치 이동
1.
최대 일치 정보인 1에 해당하는 패턴 값 T를 마지막 위치로 이동
b.
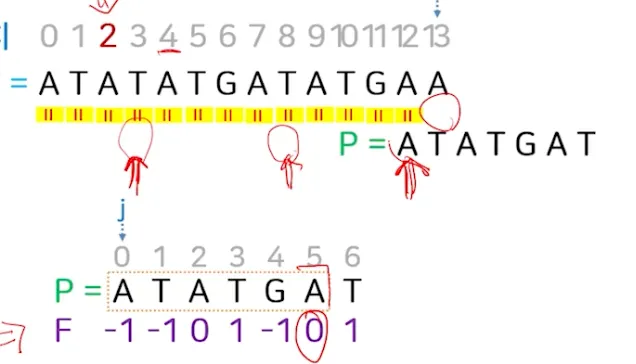
위치 4에서 일치 확인
i.
앞에 AT는 이미 일치하므로 비교 X
ii.
패턴의 마지막까지 모두 일치 확인
1.
i = 8, j = 6
2.
위치 2에서 하나의 매치 찾음
iii.
마지막 위치 (j=6)에서의 f 값(1)을 가지고 패턴의 이동 진행
1.
f = 1에 해당되는 패턴 값 = T
c.
위치 7에서 일치 확인
i.
마지막 위치에서 불일치 발생
1.
마지막 위치가 빠진 j = 5에서 일치 발생
2.
이때 f= 0
ii.
f = 0 에 하는 패턴 값이 마지막 일치 위치로 이동
d.
또다시 불일치 발생
i.
일치된 패턴이 첫번째 문자 1개밖에 없음
ii.
이 경우 f = -1 이므로 1칸만 이동
e.
전체 인덱스를 초과하므로 탐색 종료
4.4. 성능과 특징
•
전처리 O(m)
•
매칭 O(n)
•
n≥m → 전체 성능 O(n)
4.5. 레퍼런스
•
KMP 알고리즘 설명 참고하면 좋은 블로그
5. 보이어-무어 알고리즘 (Boyer-Moore)
5.1. 개념
•
패턴 내의 문자들의 관계를 이용하여 매칭 시 중복된 비교를 줄임
•
텍스트의 첫 위치에서 패턴의 뒷부분부터 문자 비교
•
불일치 또는 매치 발생 → 패턴 이동
◦
불일치 문자 방법, 일치 접미부 방법 중 더 많이 이동시킬 수 있는 값 선택
5.2. 불일치 문자 방법 (bad character)
•
불일치가 발생한 텍스트의 문자가 패턴에서 가장 마지막에 나타나는 위치가 불일치가 발생한 곳으로 오도록 패턴을 이동
•
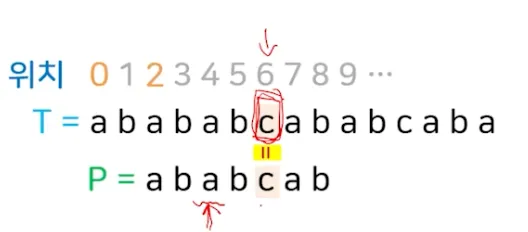
예시)
◦
불일치가 발생한 텍스트의 문자 C
◦
패턴에서 텍스트 C의 마지막 위치는 뒤에서 3번째
◦
C라는 텍스트의 문자가 서로 일치되도록 2칸 만큼 이동
5.3. 일치 접미부 방법 (good suffix)
•
일치한 서브스트링(접미부)에 대한 접두부와 접미부의 최대 일치 정보 활용
◦
KMP 알고리즘과 유사하면서도 다름
◦
KMP는 왼쪽(앞쪽)부터 비교 / 보이어 무어는 항상 뒤에서부터 비교
5.4. 알고리즘
•
불일치 문자
◦
예시)
BadChar(m, P[], Σ)
{
for (알파벳의 각 문자 c)
δ₁[c] = -1; // -1로 배열 초기화 (패턴에 없는 경우 대비)
for (i = 0; i < m; i++)
δ₁[P[i]] = i; // 패턴에서 가장 마지막에 나타나는 위치만 남김
return (δ₁);
}
C
복사
•
일치 접미부
GoodSuf (m, P[])
{
revP = P를 뒤집은 문자열;
revF[0..m-1] = PreKMP (m, revP); // 뒤집은 패턴의 최대 일치 정보 찾기
for (i=-1; i < m; i++)
δ₂[i] = m-1 - revF[m-1]; // 전체 일치인 경우의 이동값으로 배열 초기화
for (k=m-1; k >= 0; k--)
δ₂[m-1-revF[k]-1] = k - revF[k];
return (δ₂);
}
C
복사
•
보이어 무어
BM(n, T[], m, P[], Σ)
{
δ₁ = BadChar(m, P, Σ);
δ₂ = GoodSuf(m, P);
i = m - 1;
while (i < n) {
j = m - 1; // 패턴의 마지막 문자부터 시작
while (j >= 0 && P[j] == T[i]) {
i--;
j--;
}
if (j == -1) {
위치 i+1 출력; // 매치 발견
i += δ₂[-1] + m; // 전체 일치인 경우로 이동
} else {
// 불일치 문자 정보와 일치 접미부 정보 중
i += max(j - δ₁[T[i]], δ₂[j]) + m - 1 - j; // 큰 값만큼 이동
}
}
}
C
복사
5.5. 성능과 특징
•
전처리 O(m)
◦
불일치 문자 방법 O(m+|∑|)
▪
알파벳 크기(|∑|)와 패턴 길이(m)만큼 반복
◦
일치 접미부 방법
▪
KMP 알고리즘의 전처리 → O(m)
▪
패턴의 길이(m)만큼 두 번 반복
•
최악의 시간 복잡도 O(nm)
◦
텍스트 길이 x 패턴의 길이
◦
모든 위치에서 매치가 발생하는 경우
•
최선의 시간 복잡도 O(n/m)