Total
Search
1. 탐색
•
탐색이란?
◦
여러 개의 원소로 구성된 데이터에서 원하는 값을 갖는 원소를 찾는 것
▪
데이터의 형태 → 리스트, 트리, 그래프 등
▪
내부 탐색 vs 외부 탐색
▪
관련 연산 → 탐색 + (초기화, 삽입, 삭제)
•
탐색 방법
◦
리스트: 순차 탐색, 이진 탐색
◦
트리: 이진 탐색 트리, 2-3-4 트리, 레드-블랙 트리, B-트리
◦
해시 테이블: 해시 함수, 충돌 해결 방법
2. 순차 탐색
2.1. 개념
•
리스트에 있는 원소를 처음부터 차례대로 비교하여 원하는 값을 가진 원소를 찾는 방법
2.2. 특징
•
시간 복잡도
◦
탐색, 삭제 연산 시간 복잡도 O(n)
◦
삽입 연산 시간 복잡도 O(1)
•
특징
◦
정렬 되지 않고 크기가 작은 데이터에 적합
◦
모든 형태의 리스트(정렬·비정렬)에 적용 가능
◦
데이터 크기가 커질수록 탐색 시간이 급격히 증가(선형 탐색)
2. 이진 탐색
2.1. 개념
•
정렬된 리스트에서 중간값을 기준으로 원소를 찾고자 하는 값과 비교하여 탐색 범위를 절반씩 줄여 나가는 방법
•
분할 정복(divide and conquer) 기법 적용.
2.2. 탐색 방법
•
배열의 가운데 원소 A[mid]와 찾고자 하는 키(key)를 비교
1.
A[mid] == key인 경우 → 탐색 성공 (인덱스 mid를 반환 후 종료)
2.
key < A[mid]인 경우 → 왼쪽 절반 구간으로 탐색을 범위 축소
3.
A[mid] < key인 경우 → 오른쪽 절반 구간으로 탐색을 범위 축소
•
이 과정을 반복할 때마다 탐색 대상의 원소 개수가 절반씩 줄어듦
◦
탐색 시간 복잡도는 O(logn)
2.3. 특징
•
시간 복잡도
◦
탐색: O(logn)
◦
리스트 초기 정렬: O(nlogn)
◦
삽입/삭제: O(n) (정렬 유지 필요로 인한 데이터 이동 발생)
•
장단점
◦
정렬된 상태라면 빠른 탐색 가능
◦
정렬된 리스트에만 적용 가능하며, 삽입/삭제 연산이 잦은 경우 비효율적(데이터 이동 비용 큼)
•
기타
◦
주어진 배열이 정렬되어 있지 않으면 정렬 수행 필요
◦
연결 리스트 구조에서는 이진 탐색 자체가 불가능
▪
중간 값을 찾기 위해서는 직접 접근이 필요한데 연결 리스트에서는 불가
▪
따라서 항상 정렬된 배열에서만 가능
2.4. 예시 코드
def binary_search(A, key, left, right):
"""
A: 정렬된 리스트
key: 찾고자 하는 값
left: 탐색 범위의 시작 인덱스
right: 탐색 범위의 끝 인덱스
반환값: key를 가진 원소의 인덱스 (없으면 -1)
"""
if left > right: # 탐색 범위가 없는 경우
return -1
mid = (left + right) // 2 # (left + right) / 2 의 정수 몫
if A[mid] == key: # 원하는 값을 찾았으면 인덱스 mid 반환
return mid
elif key < A[mid]: # 왼쪽 부분을 재귀 탐색
return binary_search(A, key, left, mid - 1)
else: # 오른쪽 부분을 재귀 탐색
return binary_search(A, key, mid + 1, right)
# 테스트 코드 예시
if __name__ == "__main__":
# 정렬된 리스트 (예시)
arr = [2, 4, 7, 12, 15, 21, 32, 47]
key = 15
index = binary_search(arr, key, 0, len(arr) - 1)
if index != -1:
print(f"값 {key} 은(는) 인덱스 {index} 에서 찾았습니다.")
else:
print(f"값 {key} 을(를) 찾을 수 없습니다.")
Python
복사
3. 이진 탐색 트리
3.1. 개념
•
이진 트리
◦
왼쪽 서브트리에 있는 모든 키 값은 해당 노드의 키 값보다 작다.
◦
오른쪽 서브트리에 있는 모든 키 값은 해당 노드의 키 값보다 크다.
•
이진 트리 노드 구조
◦
키 값(key)
◦
왼쪽 자식 포인터(left)
◦
오른쪽 자식 포인터(right)
struct node {
struct node *left; // 왼쪽 자식 노드를 가리키는 포인터
int key; // 노드에 저장되는 실제 데이터(키 값)
struct node *right; // 오른쪽 자식 노드를 가리키는 포인터
};
C
복사
3.2. 연산
•
탐색
◦
루트 노드부터 시작하여 값의 크기에 따라 왼쪽/오른쪽 서브트리로 내려감
•
삽입
◦
삽입 위치를 먼저 탐색한 뒤(탐색 실패 지점), 해당 위치에 새 노드를 추가
•
삭제
◦
후속자(successor) 노드
▪
어떤 노드의 바로 다음 키 값을 갖는 노드
◦
삭제 노드의 자식 노드 개수에 따라 3가지 경우 (자식 0/1/2개)로 나누어 처리
▪
자식 노드가 없는 경우 (리프 노드)
•
남는 노드가 없어 위치 조절이 불 필요
▪
자식 노드가 하나인 경우
•
자식 노드를 삭제되는 노드의 위치로 올리면서 서브트리 전체도 따로 올림
▪
자식 노드가 2개인 경우
•
삭제되는 노드의 후속자 노드를 삭제되는 노드의 위치로 올리고
•
후속자 노드를 삭제되는 노드로 취급하여 자식의 노드 개수에 따라 다시 처리
3.3. 특징
•
성능
◦
평균: O(logn)
◦
최악(경사 트리 형태): O(n)
•
장단점
◦
삽입/삭제 시 전체 노드를 재정렬하거나 이동할 필요가 거의 없음(트리 구조)
◦
삽입/삭제가 반복되어 트리가 한쪽으로 치우치면 성능이 급격히 나빠질 수 있음
→ 경사 트리가 만들어지지 않도록 트리 균형을 위해 O(logn)을 보장
▪
균형 탐색 트리 (2-3-4 트리, 레드-블랙 트리, B-트리)
4. 2-3-4 트리
4.1. 개념
•
다음 성질을 만족하는 균형 탐색 트리
◦
2-노드 → 1개의 키와 2개의 자식을 갖는 노드
◦
3-노드 → 2개의 키와 3개의 자식을 갖는 노드
◦
4-노드 → 3개의 키와 4개의 자식을 갖는 노드
◦
각 노드의 한 키의 왼쪽 서브트리에 있는 모든 키 값은 그 키 값보다 작다.
◦
각 노드의 한 키의 오른쪽 서브트리에 있는 모든 키 값은 그 키 값보다 크다.
◦
모든 리프 노드의 레벨은 동일
•
예시)
4.2. 연산
•
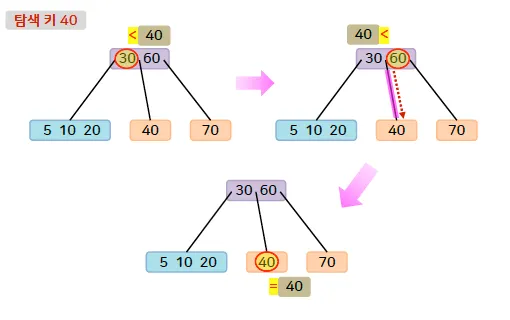
탐색 연산
•
삽입 연산
◦
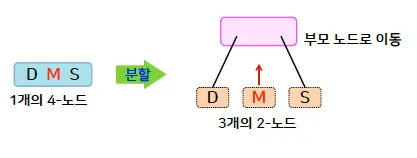
탐색 과정에서 4-노드를 만나면 항상 노드 분할을 우선 수행
◦
노드 분할
◦
노드 분할의 유형
4.3. 특징
•
성능
◦
탐색/삽입/삭제: O(logn)
•
장단점
◦
항상 균형 상태를 유지하므로 삽입·삭제·탐색 모두 안정적인 O(logn) 보장
◦
노드 구조가 복잡하여 실제 구현 시 오버헤드가 많을 수 있으며, 단순 이진 탐색 트리보다 느려질 가능성이 있음