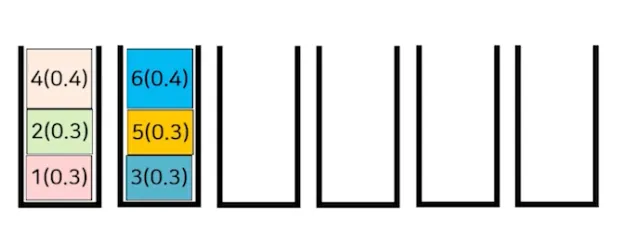Total
Search
1. 기본 개념
1.1. NP-완전문제?
•
다음을 모두 만족하는 문제 A
◦
클래스 NP에 속하는 모든 문제가 문제 A로 다항 시간에 변환됨
◦
문제 A가 클래스 NP에 속함
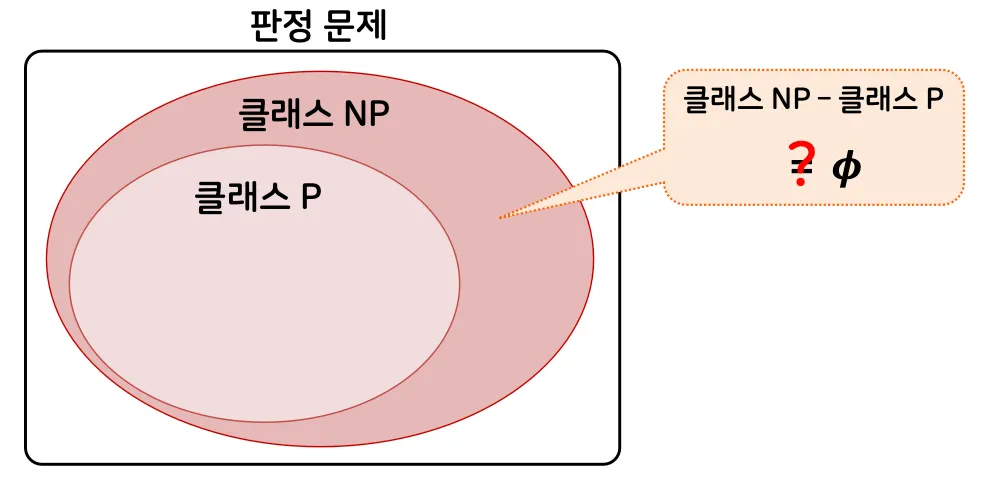
1.2. 클래스 NP
•
개념
◦
비결정론적 튜링 기계를 이용하여 다항 시간에 해결할 수 있는 모든 판정 문제의 집합
•
비결정론적 튜링 기계
◦
헤드의 위치를 바꾸거나 테이프에 쓰인 기호를 바꿀 때 하나 이상의 상태로 바뀔 수 있거나 혹은 바뀔 상태가 없을 수 있는 튜링 기계
•
다항 시간 알고리즘
◦
알고리즘의 수행시간이 입력 크기에 대한 다항식으로 표현됨
◦
예) O(1), O(logn), O(n), O(nlogn), O(n^2), O(n^3)
◦
cf) 지수 시간 알고리즘 O(2^n), O(3^n)
▪
다항 시간의 반대
•
판정 문제
◦
‘예’ 또는 ‘아니요’ 중 하나를 답으로 요구하는 문제
◦
cf) 최적화 문제
▪
최솟값 또는 최댓값을 구하는 형태의 문제
•
클래스 P
◦
결정론적 튜링 기계를 이용하여 다항 시간에 해결할 수 있는 모든 판정 문제의 집합
•
판정문제의 다이어그램
1.3. 변환
•
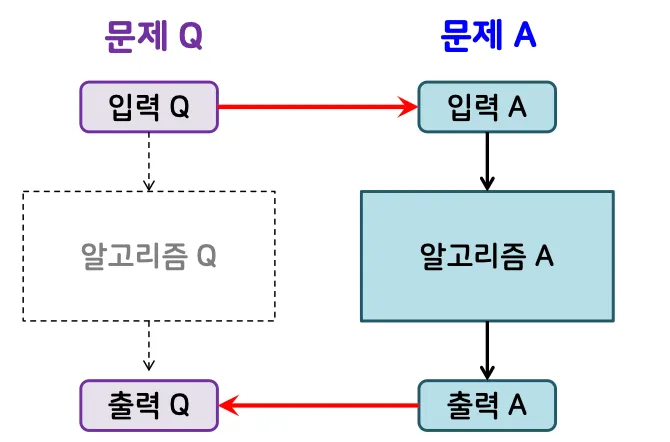
문제 Q가 문제 A로 변환됨
◦
문제 Q의 입력과 출력을 문제 A의 입력과 출력 형태로 바꿀 수 있고
◦
여기에 문제 A를 해결하는 알고리즘을 적용하여 문제 Q를 해결 가능
•
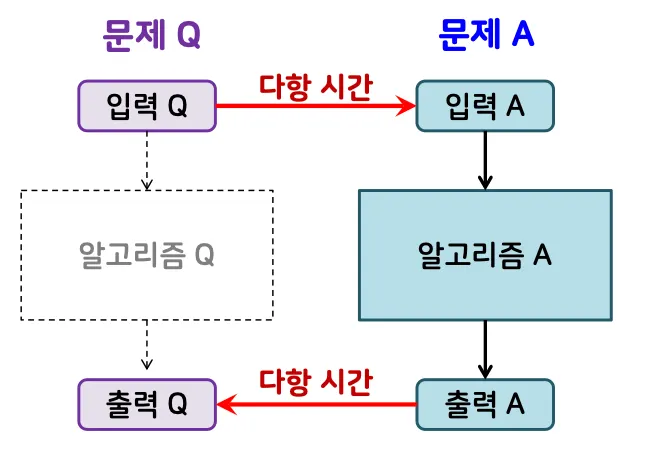
문제 Q가 문제 A로 다항시간에 변환됨
◦
문제 Q의 입력과 출력을 문제 A의 입력과 출력 형태로 다항 시간에 바꿀 수 있고
◦
여기에 문제 A를 해결하는 알고리즘을 적용하여 문제 Q를 해결 가능
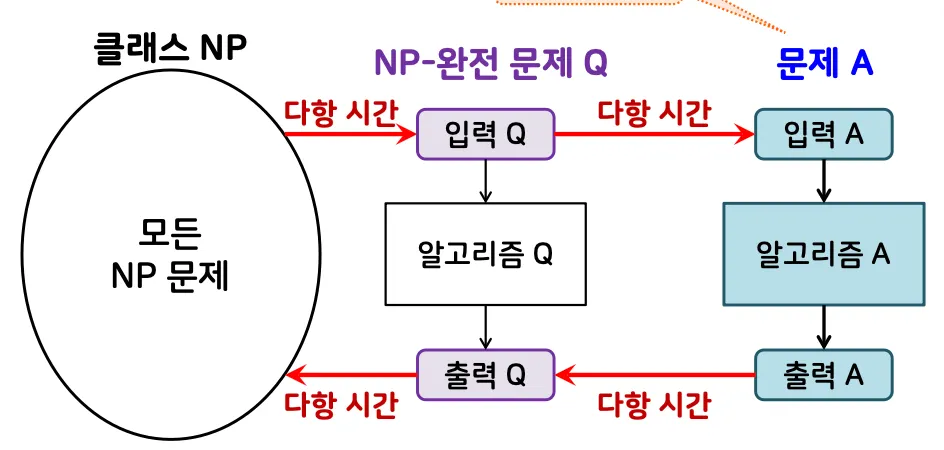
1.4. NP-완전 문제
•
다음을 모두 만족하는 문제 A
◦
클래스 NP에 속하는 모든 문제가 문제 A로 다항 시간에 변환됨
◦
문제 A가 클래스 NP에 속함 → 문제 A는 판정 문제이어야 함
•
NP-완전 문제 예시
◦
CNF 만족성 문제
◦
클리크 판정 문제
◦
버텍스 커버 문제
◦
해밀토니언 사이클 문제
◦
외판원 문제
◦
통 채우기 문제
2. 근사 알고리즘
2.1. 개념
•
최적화 문제에 대하여 최적의 해에 가까운 근사해를 다항 시간에 구하는 알고리즘
•
NP-하드 문제에 많이 이용됨
•
NP-하드 문제
◦
클래스 NP에 속하는 모든 문제가 그 문제로 다항 시간에 변환되는 문제
◦
모든 NP-완전 문제는 NP-하드 문제임
•
cf) NP-하드 문제이지만 NP-완전 문제가 아닌 경우
◦
판정 문제가 아닌 최적화 문제
◦
판정 문제이지만 클래스 NP에 속하지 못하는 정지(halting) 문제 등
2.2. 버텍스 커버 문제
•
주어진 그래프의 모든 간선과 맞닿은 최소 크기의 정점의 부분 집합을 찾는 문제
◦
{a,c}, {b,c}, {b,d} 크기가 2 (최소 크기) 이며 모든 간선과 맞닿음
•
근사 알고리즘
◦
선택한 간선의 양 끝 정점을 포함시키는 방식
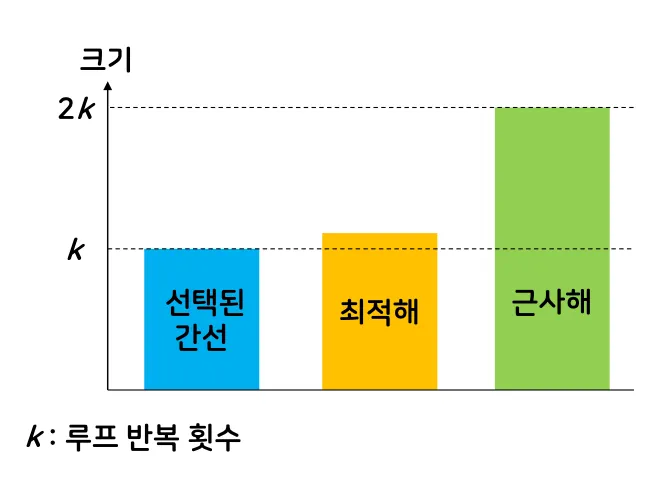
◦
근사해는 최적해의 두 배가 넘지 않음
◦
시간 복잡도 O(|E|)
ApproxVertexCover (G)
{
int Size = 0;
while (E ≠ ∅) { // C[]와 맞닿지 않은 간선이 존재하는 동안
e = E에 속하는 임의의 간선 (u, v);
// 선택한 간선의 두 정점을 C[]에 추가
C[++Size] = e.u;
C[++Size] = e.v;
E에서 u에 맞닿은 모든 간선과 v에 맞닿은 모든 간선을 제거;
}
return C[];
}
C
복사
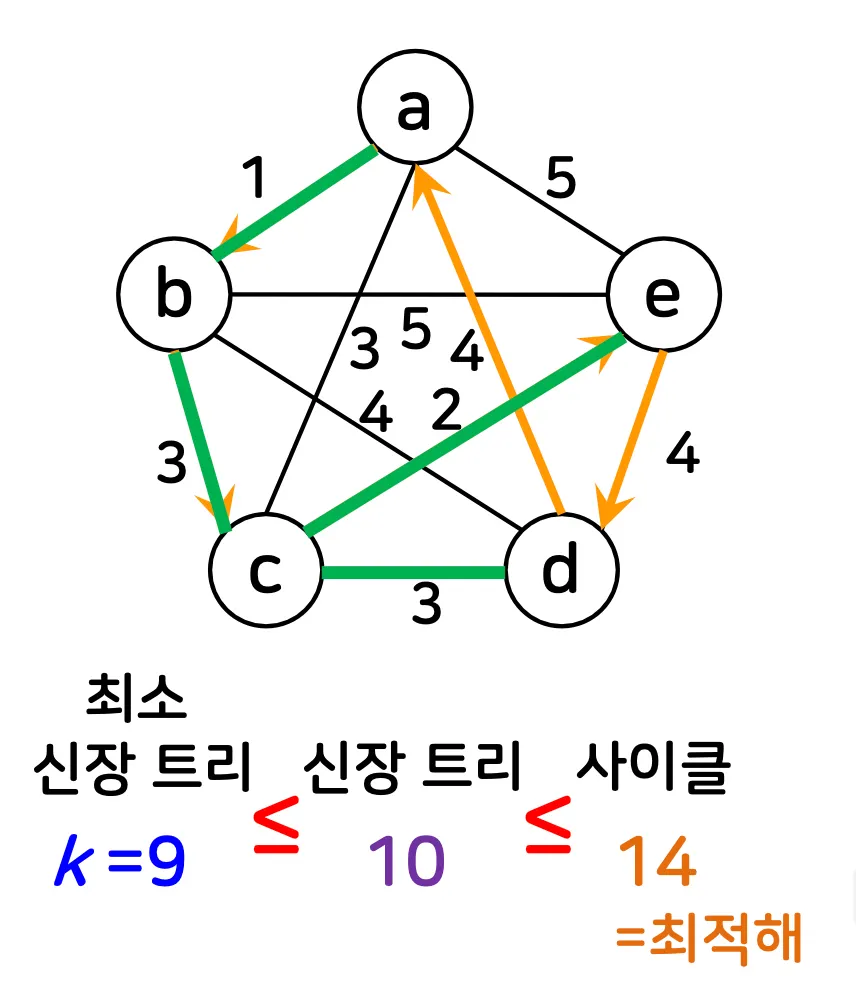
2.3. 외판원 문제 (TSP)
•
개념
◦
여러 도시 및 도시 간의 이동에 필요한 비용이 주어진 경우 최소 비용으로 모든 도시를 한 번씩만 방문하고 처음 도시로 돌아오는 방법을 찾는 문제
•
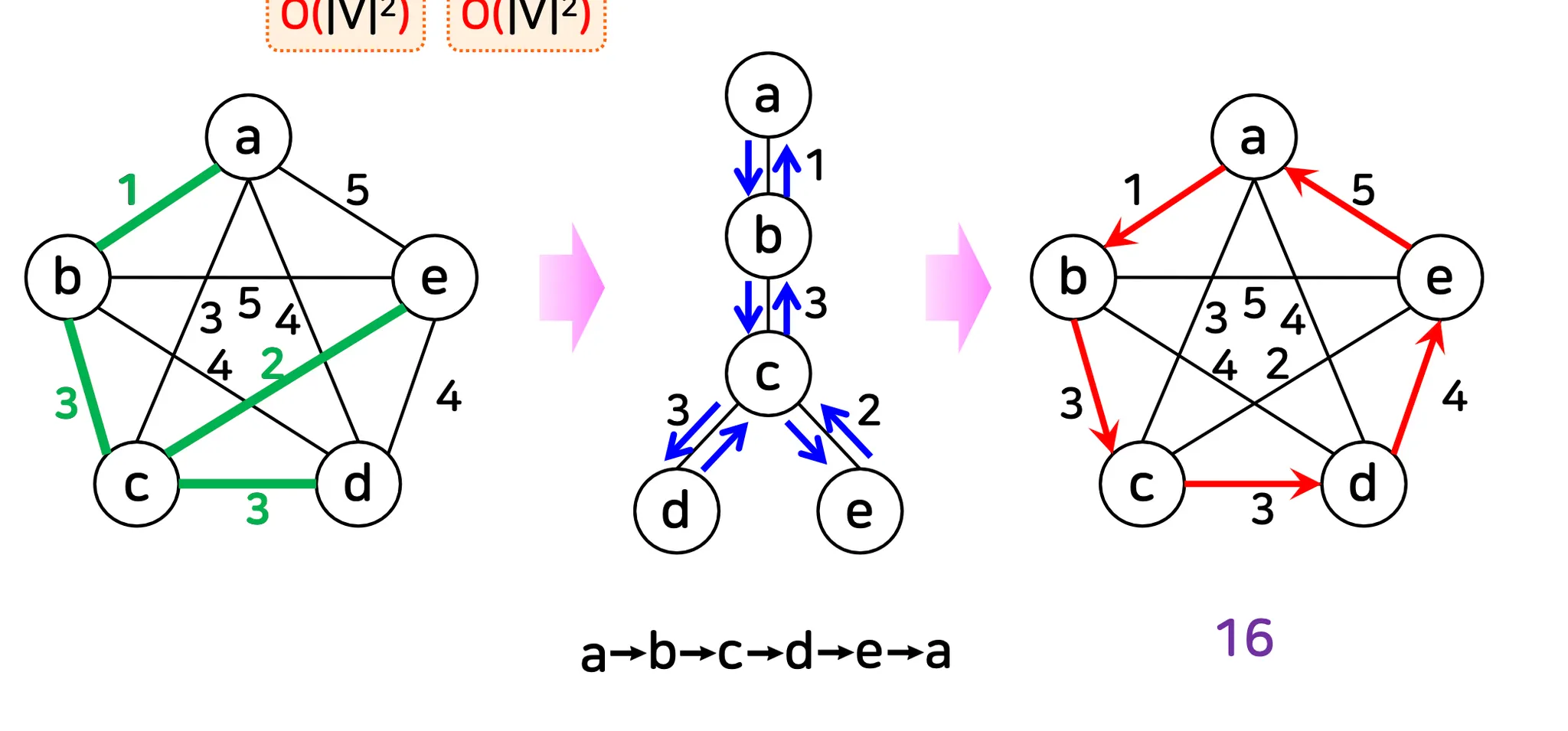
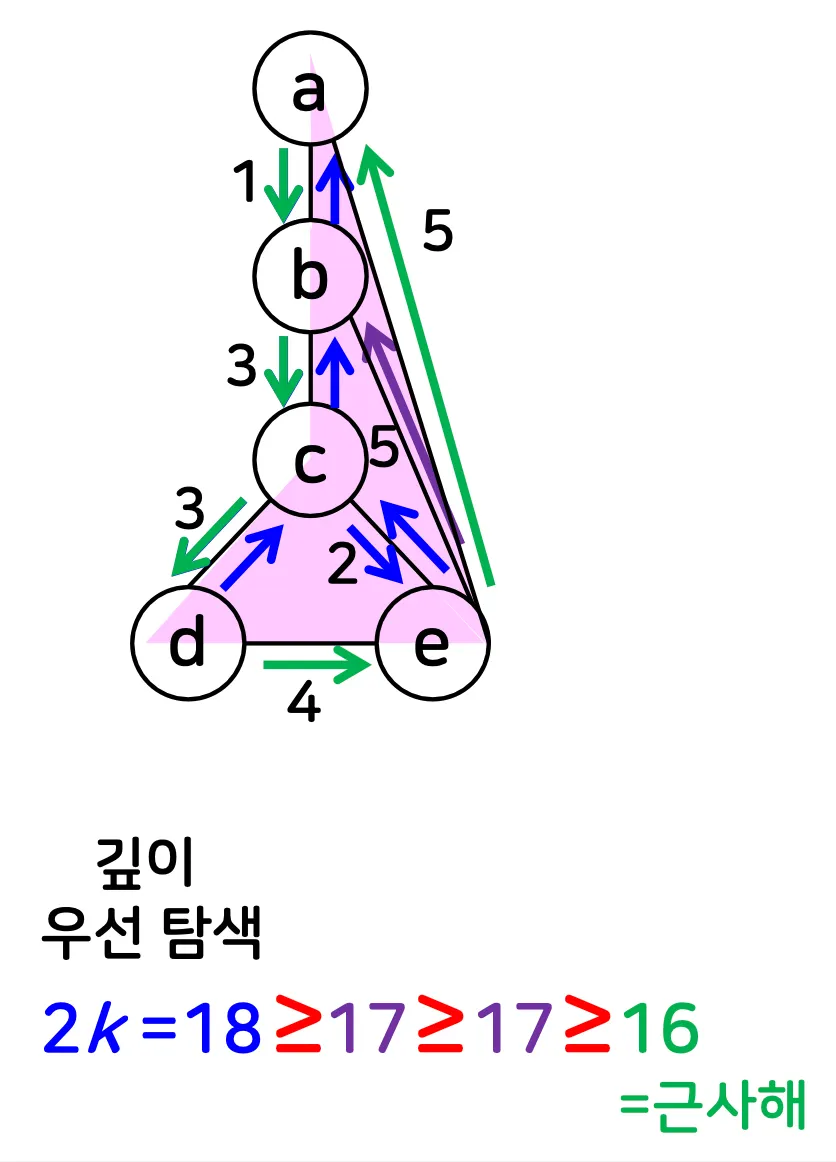
근사 알고리즘
◦
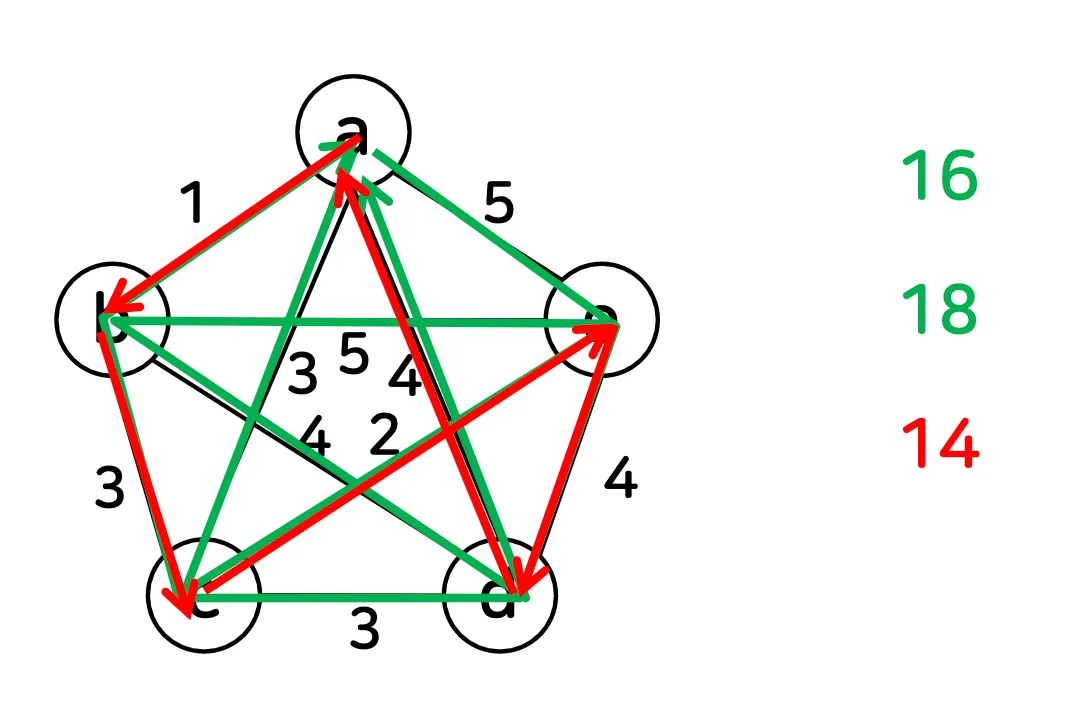
최소 신장 트리(O(|V|^2)와 깊이 우선 탐색(O(|V|^2)을 이용하는 방식
◦
cf) 최척해: 14
•
근사 알고리즘의 특징
◦
가정 → 이동 비용이 삼각부등식을 만족
▪
삼각부등식
•
삼각형의 두변의 합이 다른 한변보다 크거나 같다.
•
a + b ≥ c
•
b + c ≥ a
•
c + a ≥ b
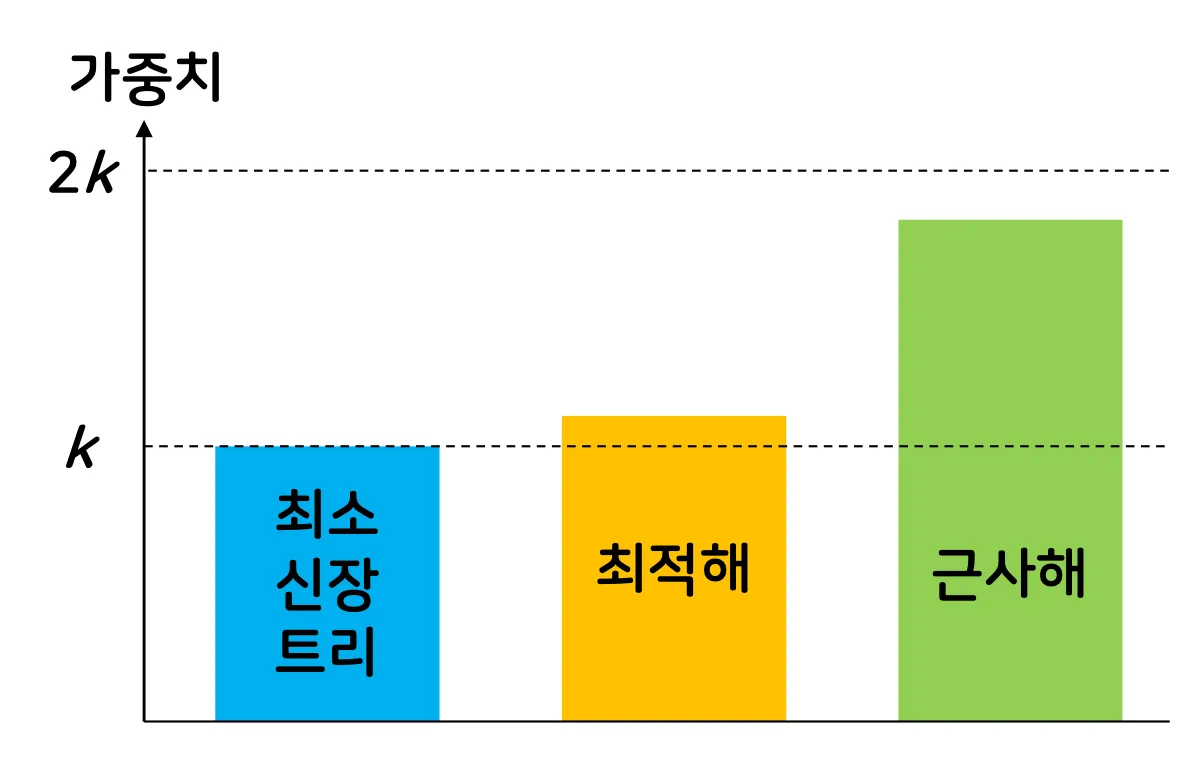
◦
근사해는 최적해의 두 배가 넘지 않음
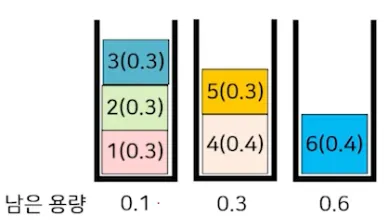
2.4. 통 채우기 문제
•
주어진 다양한 크기의 물체 n개를 최소 개수의 통에 넣는 문제
◦
가정 → 통 크기 1, 물체 크기 0 이상 1 이하
•
근사 알고리즘
◦
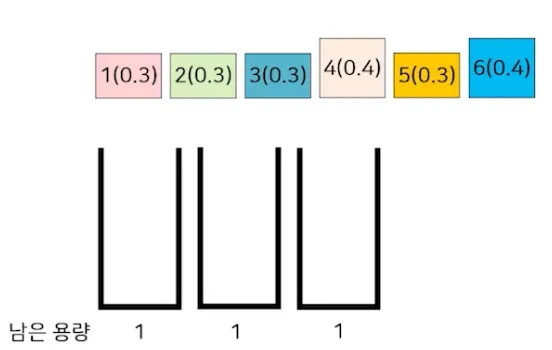
최초법
▪
선택한 물체O(n))를 넣을 수 있는 최초의 통에 넣는 (O(n)) 방식
▪
선택할 물체 탐색 O(n) + 넣을 통 탐색 O(n) → O(n^2)
◦
감소순 최초법
▪
물체들을 크기의 감소순으로 정렬 후 최초법을 적용하는 방식
▪
감소순 정렬 O(nlogn) + 최초법 O(n^2) → O(n^2)
◦
최선법
▪
선택한 물체를 넣었을 때 남는 부분이 가장 작은 통에 넣는 방식
▪
선택할 물체 탐색 O(n) + 남는 부분이 가장 작은 넣을 통 탐색 O(n) → O(n^2)
◦
감소순 최선법
▪
물체들을 크기의 감소순으로 정렬 후 최선법을 적용하는 방식
▪
감소순 정렬 O(nlogn) + 최선법 O(n^2) → O(n^2)
•
근사 알고리즘의 특징
◦
근사해는 최적해의 두 배가 넘지 않음
◦
최초법, 최선법 → 근사해는 최적해의 약 1.7배가 넘지 않음
◦
감소순 최초법, 감소순 최선법 → 근사해는 최적해의 약 1.3배가 넘지 않음