Total
Search
1. 동적 프로그래밍의 기본 개념
1.1. 개념
•
정의
◦
문제를 작은 소문제(sub-problems)로 나누고, 이들의 해를 테이블에 저장하여 상위 문제의 해를 점진적으로 도출하는 상향식(bottom-up) 접근법
◦
소문제는 원래 문제와 동일하지만 입력 크기만 작음.
◦
최적화 문제(최솟값 또는 최댓값을 구하는 문제)에 주로 사용됨.
•
핵심 특징
◦
소문제는 독립적일 필요가 없으며 중복 가능.
◦
최적성의 원리(Principle of Optimality)
▪
"큰 문제의 최적해는 작은 소문제의 최적해로 구성됨."
•
처리 과정
1.
최적성 원리 확인: 문제의 특성 분석
2.
점화식 도출: 문제의 최적해를 정의
3.
소문제 계산: 점화식을 이용해 작은 소문제부터 테이블에 값 저장
4.
큰 문제 해결: 테이블 값을 참조해 최종 문제 해를 구함
1.2. 예제: 피보나치 수열
•
DP를 활용한 경우
•
재귀를 사용한 경우 → 중복된 계산으로 인해 비효율적
2. 행렬의 연쇄적 곱셈
2.1. 개념
•
정의
◦
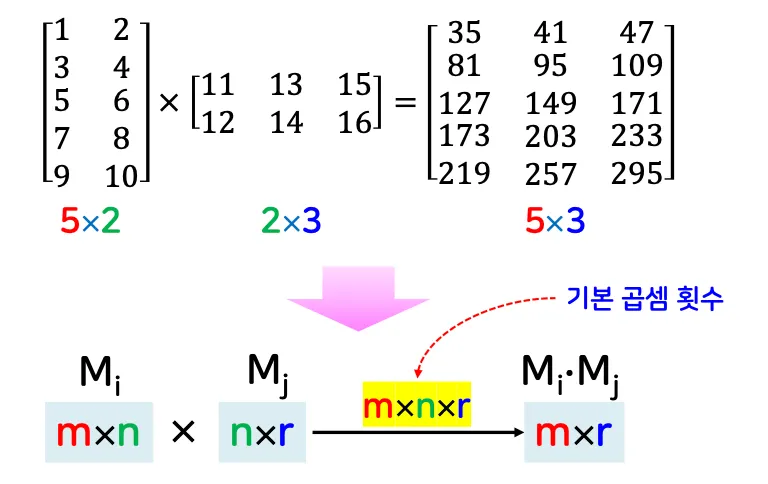
n개의 행렬 (M1,M2,...,Mn)의 곱셈에서 기본 곱셈 횟수를 최소화하는 최적의 곱셈 순서를 찾는 문제
◦
여러가지 다른 곱셈 순서가 존재할때, 순서를 어떻게 설정하냐에 따라 곱셉 횟수가 달라짐
▪
결합법칙 성립.
▪
M1*M2*M3 = (M1*M2)*M3 = M1*(M2*M3)
•
기본 곱셈
◦
행렬 원소끼리 곱셈
◦
예시
▪
결합법칙에 따라 2가지 선택지가 있음
▪
기본 곱셈 횟수가 낮은 방법을 선택하는 것이 좋음
2.2. 최적성의 원리
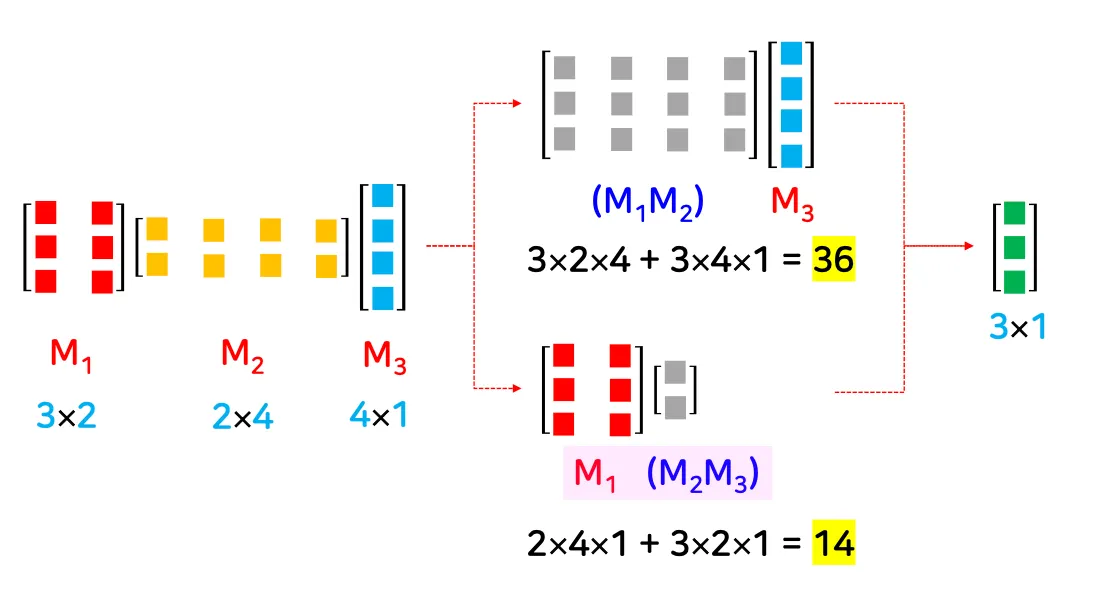
•
n개의 행렬을 곱하는 최적의 순서는 n개의 행렬의 연쇄적 곱셈 중 일부분에서 최적의 곱셈 순서를 포함
◦
부분 문제들의 최적해로 n개 행렬을 곱하는 최적의 순서를 구할 수 있음
◦
최적성의 원리 성립
◦
동적 프로그래밍으로 해결 가능
2.3. 점화식과 알고리즘
•
점화식
◦
C(i, j)에 기본 곱셈의 최소 횟수 저장
◦
가장 작은 위치의 k를 찾아야 함
▪
어디서 끊어서 2개의 곱으로 나타낼건지를 찾아야 함
▪
P(i, j) = k
•
알고리즘
// 입력: 행렬의 개수 n, 행렬의 크기 d[0..n] (i번째 행렬의 크기 d[i-1]×d[i])
// 출력: C[1][n] : n개의 행렬을 곱하는 데 필요한 기본 곱셈 횟수의 최소값
// P[1..n][1..n] : 최적의 곱셈 순서를 구할 수 있는 배열
MinMatMult(n, d[])
{
int i, j, k, s;
int C[n+1][n+1];
for (i = 1; i <= n; i++) C[i][i] = 0;
for (s = 1; s <= n-1; s++)
for (i = 1; i <= n-s; i++) {
j = i + s;
C[i][j] = min_{i ≤ k < j}(C[i][k] + C[k+1][j] + d[i-1]d[k]d[j]);
P[i][j] = 최소값이 되는 k의 값;
}
return (C[1][n], P[1..n][1..n]);
}
C
복사
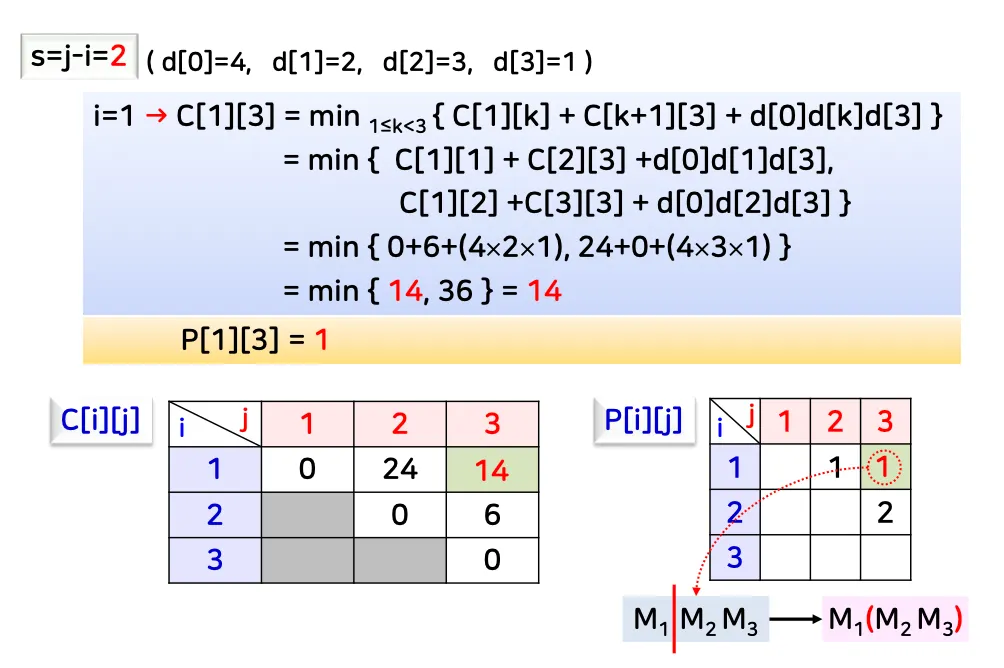
2.4. 예시
[예시 1]
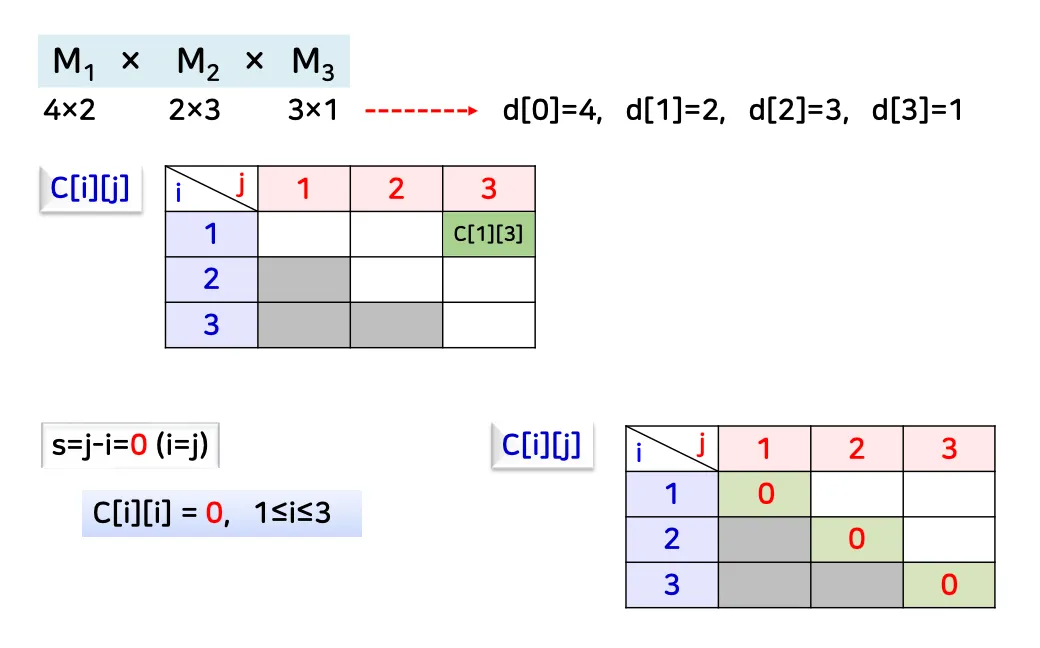
•
d: 행렬의 크기
•
c[1][3]: 우리가 찾고 싶은 값
•
c[i][i]는 기본적으로 0 (동일한 행렬이므로 곱셈의 횟수는 0)
•
k의 범위: i≤k<j
•
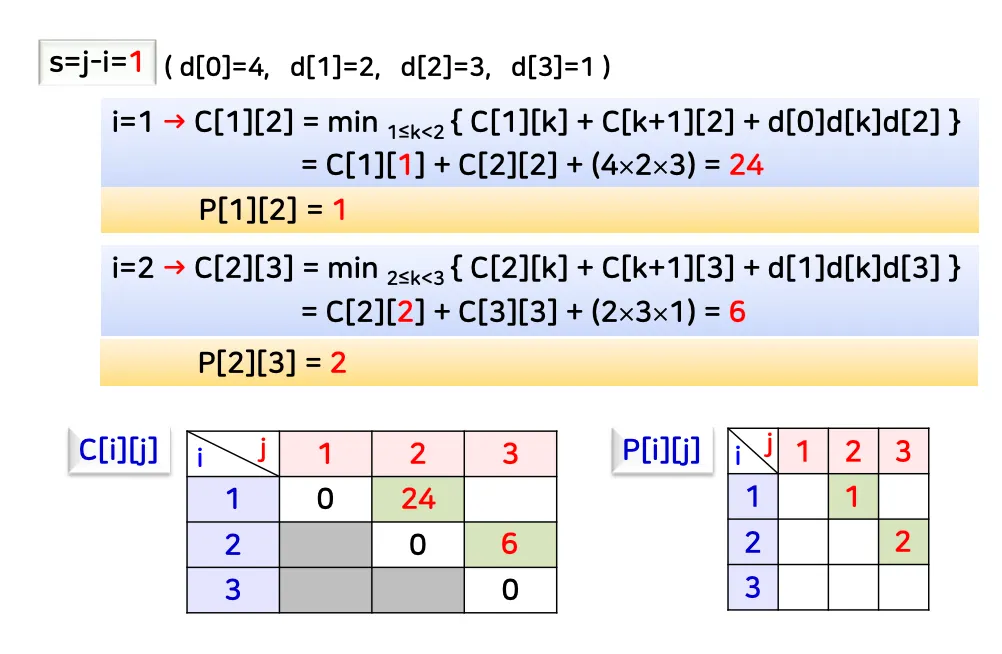
그대로 대입해서 저장
•
P[i][j]에 행렬 곱을 어디서 분리할건지를 저장
•
k의 범위가 1~3이므로 1일때, 2일때를 각각 계산하여 최소값 도출
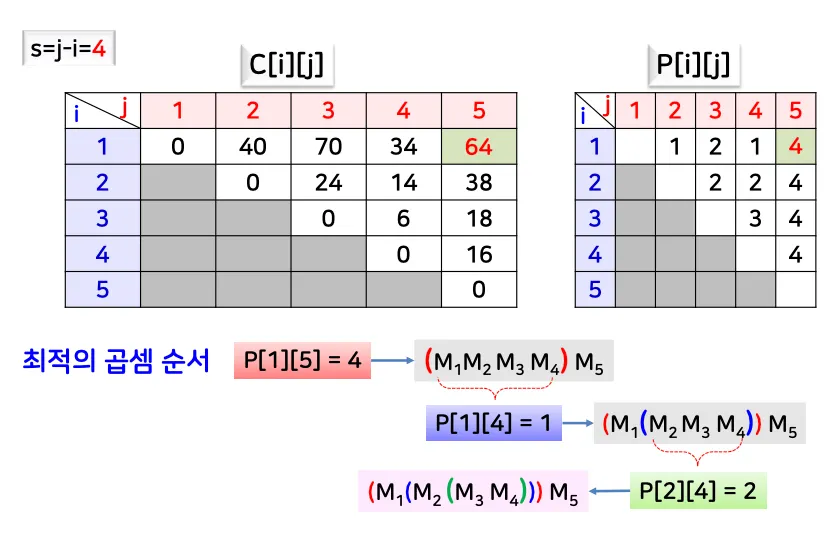
[예시 2]
•
최종 결과
2.5. 성능 및 특징
•
시간 복잡도: O(n^3)
•
최적의 행렬 곱셈 순서를 구하는 알고리즘 O(n)
◦
P[i][j]를 이용할 때마다 나뉠 부분이 하나씩 줄어듦
◦
n개 행렬의 곱셈 순서에는 n-2번의 분할 지점이 필요 O(n)
3.최장 공통 부분 수열 (LCS)
3.1. 개념
•
정의
◦
두 문자열 XX와 YY의 공통된 부분 수열 중 가장 긴 수열 찾기.
◦
부분 수열
▪
스트링에서 연속일 필요 없지만 순서는 유지되는 스트링의 일부분
•
예시
◦
X = "SNOWY", Y = "SUNNY"
◦
LCS = "SNY"
3.2. 최적성의 원리
•
두 스트링 X와 Y사이의 LCS는 이들의 어떤 서브스트링 사이의 LCS를 포함
1.
X의 마지막 글자와 Y의 마지막 글자가 같은 경우
•
X1 ~ Xn-1와 Y1 ~ Ym-1 의 LCS에 마지막 글자를 추가한 것과 같음
•
SNOWY / SNNNY → SNY
2.
X의 마지막 글자가 Y의 마지막 글자와 다르며, LCS에 사용되지 않은 경우
•
X1 ~ Xn-1와 Y1 ~ Ym 의 LCS와 동일
•
SNOW / SNNN → SN
3.
X의 마지막 글자가 Y의 마지막 글자와 다르며 LCS에 사용된 경우
(이 경우 X의 마지막 글자는 Y의 마지막 글자 이전의 다른 글자와 일치)
•
X1 ~ Xn와 Y1 ~ Ym-1 의 LCS와 동일
•
SUN / SNO → SN
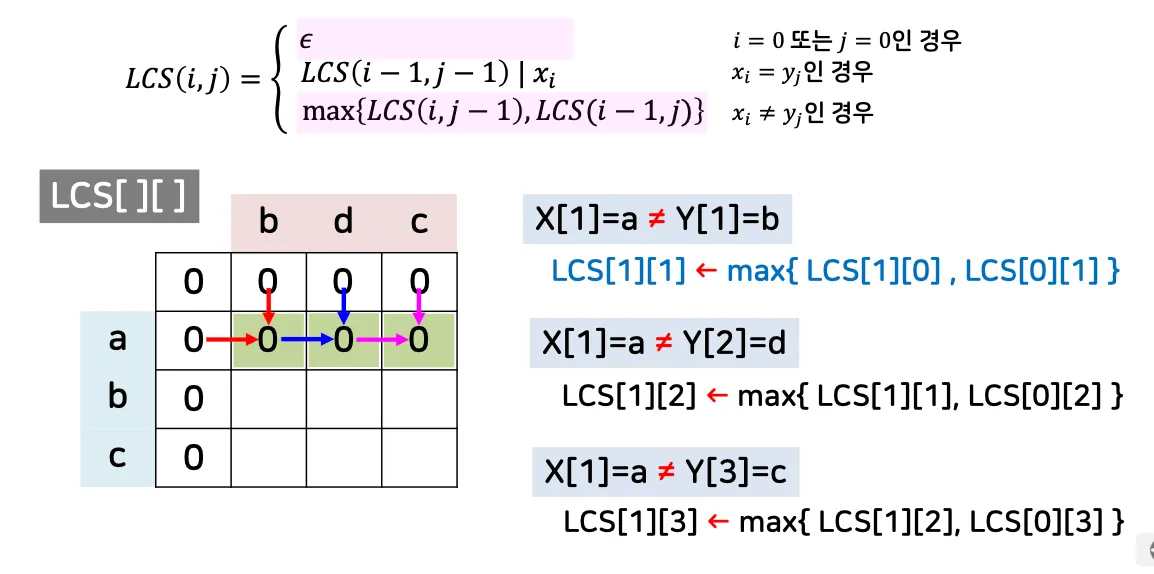
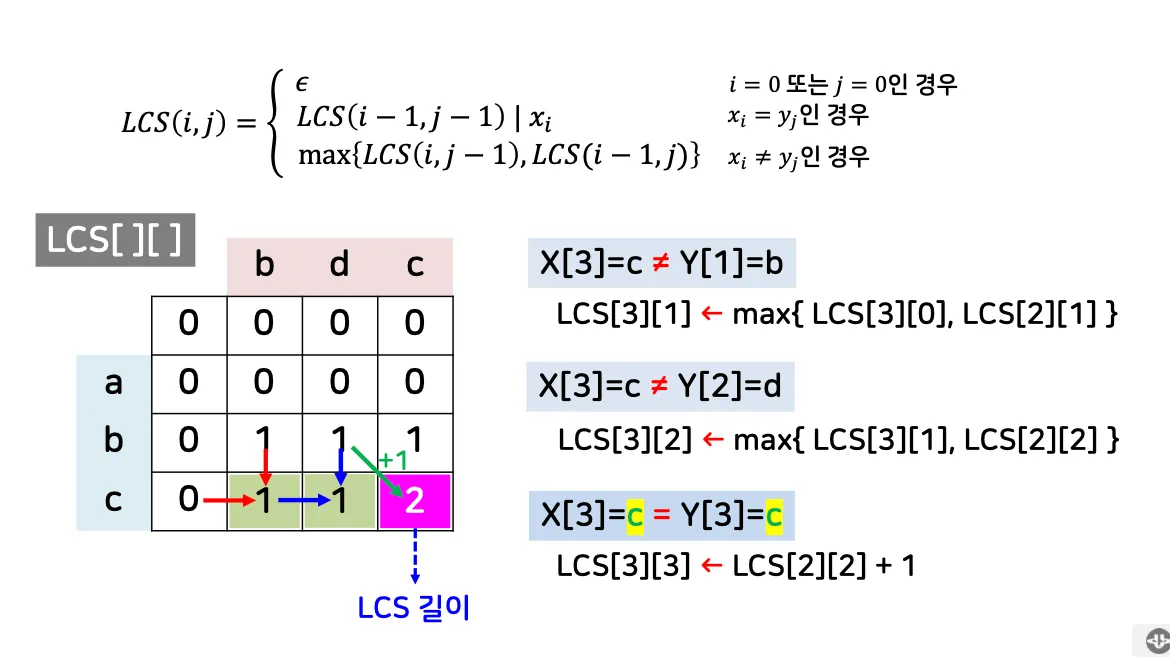
3.3. 점화식과 알고리즘
•
점화식
◦
Xi = Yi : 마지막 문자열이 같다는 것을 의미
•
알고리즘
// 입력: X[1..n], Y[1..m] : 두 스트링
// 출력: LCS[n][m] : LCS 길이
// LCS[0..n][0..m] : LCS를 구할 수 있는 배열
LCS(n, X[], m, Y[])
{
int LCS[n+1][m+1];
int i, j;
LCS[0][0] = 0; // LCS 길이 테이블 초기화
for (i = 1; i <= n; i++) LCS[i][0] = 0; // 첫 열의 초기화
for (j = 1; j <= m; j++) LCS[0][j] = 0; // 첫 행의 초기화
for (i = 1; i <= n; i++)
for (j = 1; j <= m; j++)
if (X[i] == Y[j])
LCS[i][j] = LCS[i-1][j-1] + 1;
else
LCS[i][j] = max(LCS[i-1][j], LCS[i][j-1]);
return (LCS[n][m], LCS[0..n][0..m]); // LCS 길이와 테이블 반환
}
// 입력: X[1..n], Y[1..m] : 두 스트링
// LCS[0..n][0..m] : LCS를 구할 수 있는 배열
// 출력: L : LCS
GetLCS(n, X, m, Y, LCS[][])
{
int i = n, j = m, idx = LCS[n][m];
char L[idx+1]; // LCS를 저장할 배열
while (idx > 0) { // LCS 길이만큼 반복
if (X[i] == Y[j]) {
L[idx] = X[i]; // 공통 문자를 LCS에 추가
idx--; i--; j--;
} else if (LCS[i][j-1] > LCS[i-1][j])
j--; // 큰 값 쪽으로 이동
else
i--;
}
return (L[1..LCS[n][m]]); // LCS 반환
}
C
복사
3.4. 예시
•
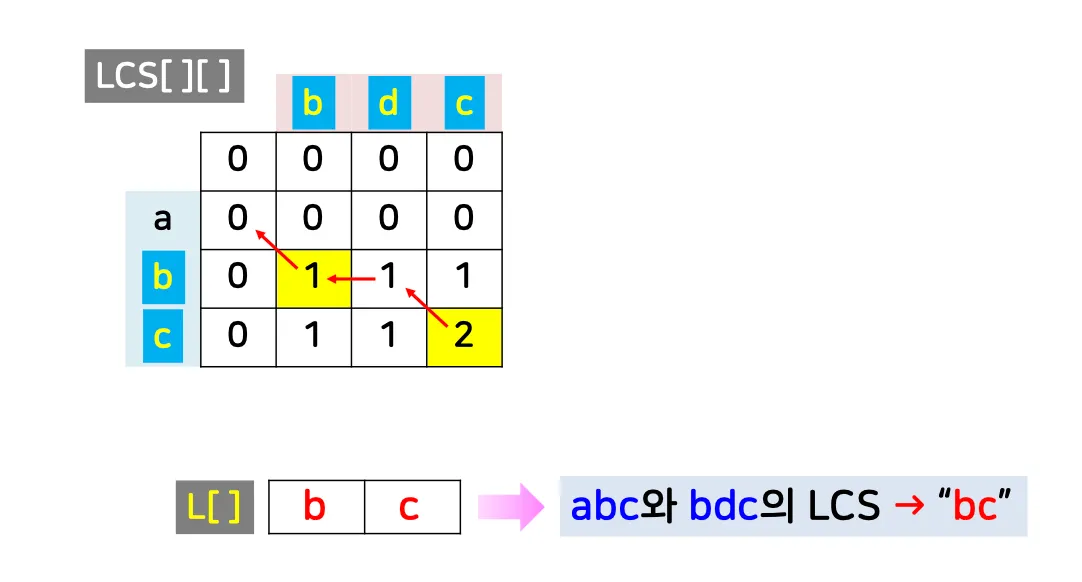
[예시 1] 스트링 X=abc와 Y=bdc의 LCS?
•
[예시 2] 스트링 X=SNOWY와 Y=SUNNY의 LCS?
3.5. 성능 및 특징
•
길이 n과 m인 두 스트링의 LCS 길이 → O(nm)
◦
각각 길이 n과 m을 사용하는 중첩된 이중 루프
•
테이블 LCS[][]로부터 LCS를 구하는 알고리즘 → O(n+m)
◦
idx가 LCS 길이만큼 줄어들 때까지 반복하는 형태의 루프로 구성
◦
실제로는 i=n, j=m부터 최대 i=0, j=0까지 도달 가능