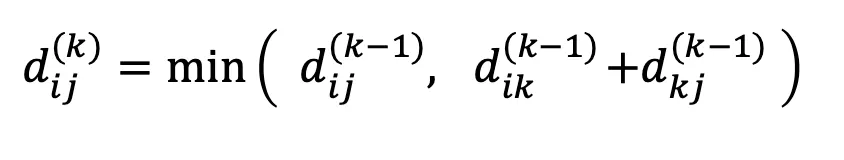Total
Search
1. 최단 경로
•
최단 경로 정의
◦
두 정점 u와 v 간의 최단 경로
◦
가중 그래프에서 두 정점 u에서 v를 연결하는 경로 중 간선의 가중치 합이 가장 작은 경로
•
최단 경로 문제 유형
◦
단일 출발점 최단 경로 문제
▪
다익스트라, 벨만 포드 알고리즘
◦
단일 도착점 최단 경로 문제
◦
단일 쌍 최단 경로 문제
◦
모든 쌍 최단 경로 문제
▪
플로이드 알고리즘
2. 데이크스트라 알고리즘
2.1. 개념
•
정의
◦
단일 출발점 최단 경로를 찾는 알고리즘.
◦
하나의 출발점 S에서 모든 정점으로의 최단 경로를 계산
◦
욕심쟁이 방법을 적용한 알고리즘으로, 음수 가중치가 없는 그래프에서만 동작
•
동작 원리
1.
초기화
•
출발점 s의 거리 d[s] = 0
•
나머지 모든 정점 v의 거리 d[v]=∞
•
선택된 정점의 집합 S = {}
2.
아직 선택되지 않은 정점 (V-S) 중에서 d[]값이 최소인 정점 u 를 선택
3.
정점 u의 인접 정점 v에 대해:
•
d[v]=min(d[v],d[u]+w(u,v))
4.
모든 정점을 처리할 때까지 반복
•
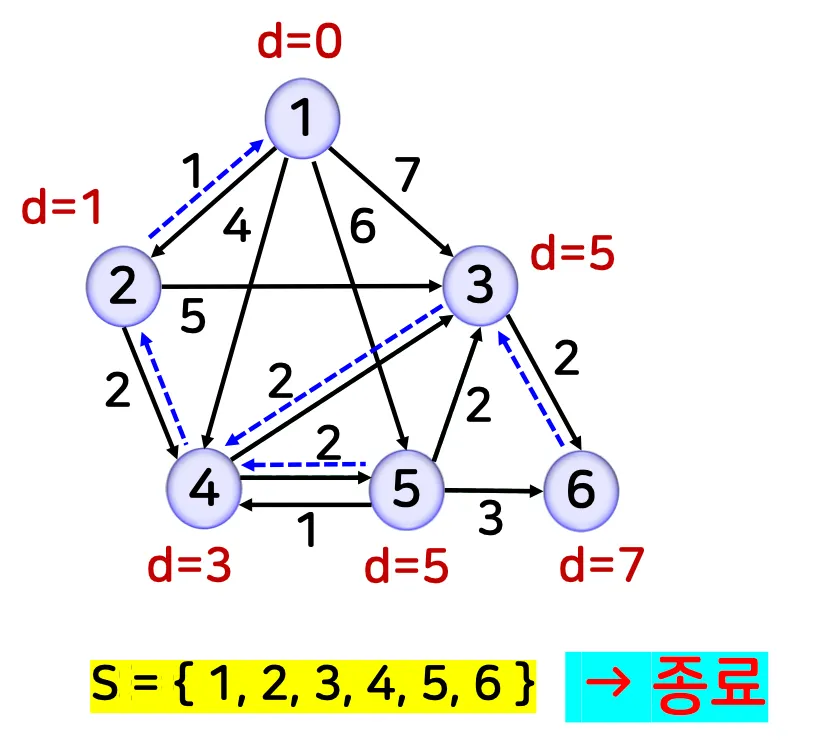
예시 1
•
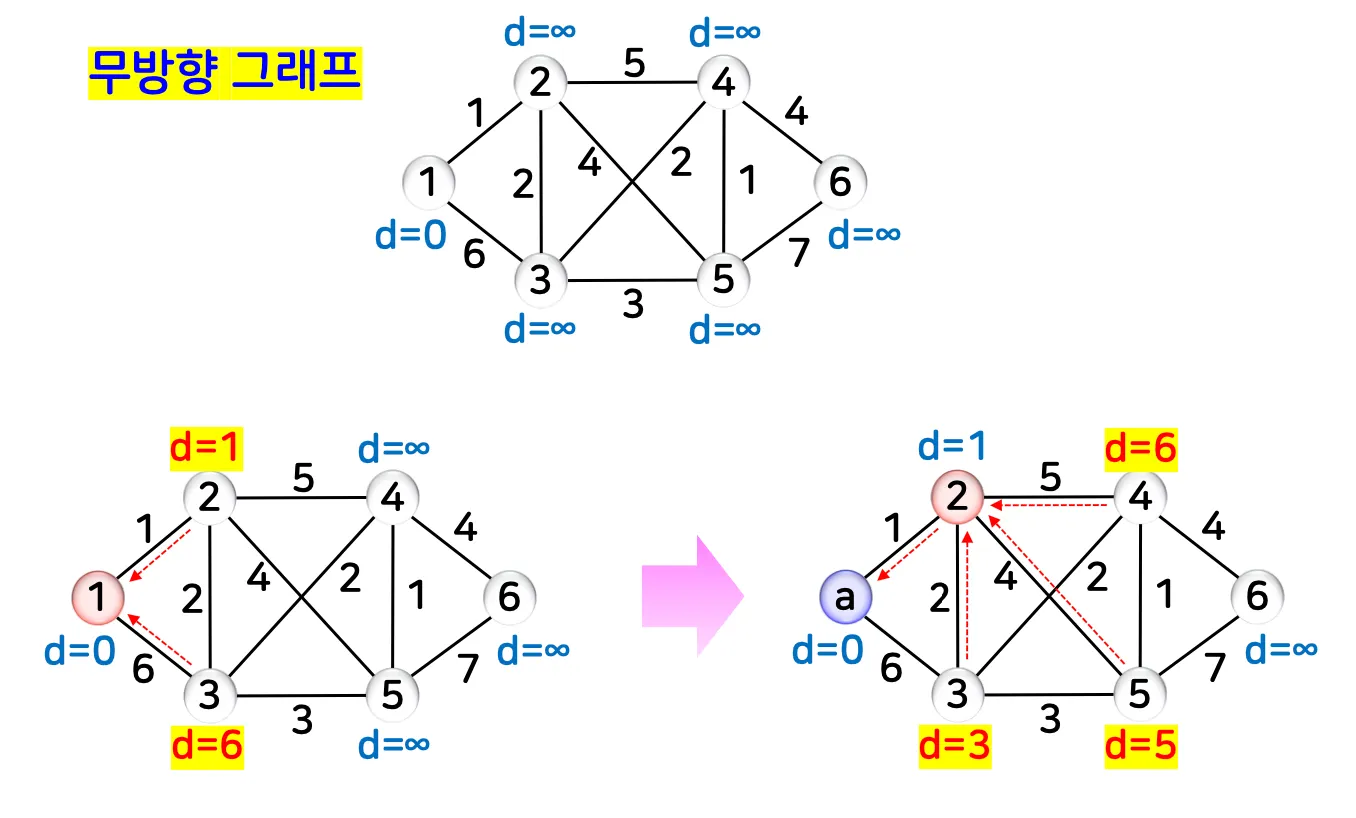
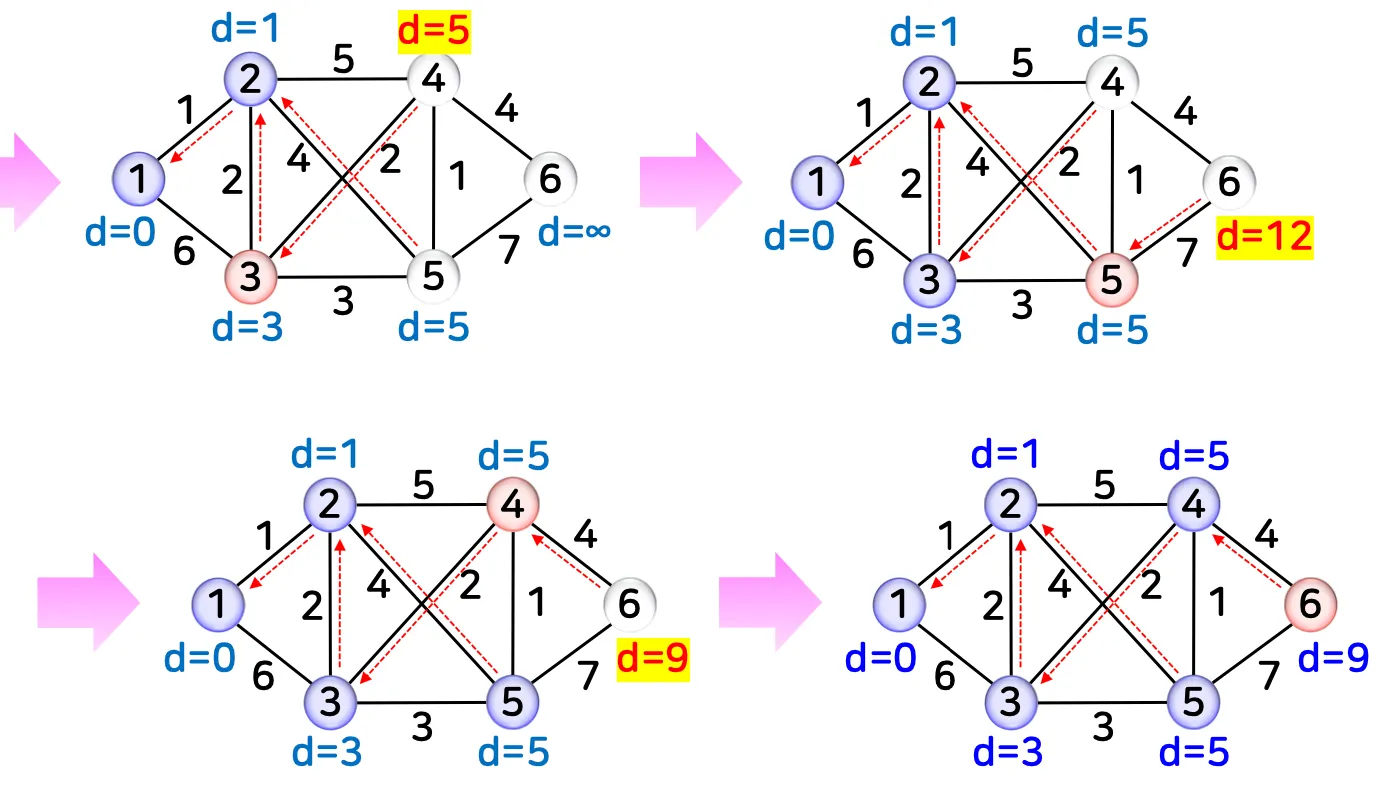
예시 2
2.2. 예시 코드
// 입력: G=(V,E), s : 시작 정점
// 출력: d[] : s로부터 다른 모든 정점으로의 최단 경로의 길이
// prev[] : 최단 경로를 만드는 선행 정점
Dijkstra (G, s)
{
S = { };
d[s] = 0;
for ( 모든 정점 v ∈ V ) {
d[v] = ∞;
prev[v] = NULL;
}
while ( S != V ) {
d[u]가 최소인 정점 u ∈ V-S를 선택;
S = S ∪ { u };
for ( u에 인접한 모든 정점 v ) {
if ( d[v] > d[u] + W(u, v) ) {
d[v] = d[u] + W(u, v);
prev[v] = u;
}
}
}
return ( d[], prev[] );
}
C
복사
import heapq
def dijkstra(graph, start):
"""
graph: 딕셔너리 형태의 인접 리스트
예) graph[u] = [(가중치, 인접정점), (가중치, 인접정점), ... ]
start: 시작 정점
return: d, prev
d[v]: start에서 v까지의 최단 거리
prev[v]: start->...->v 최단 경로에서 v 직전에 방문한 정점
"""
# 모든 정점에 대해 최단 거리 d[v] = 무한대로 초기화
d = {node: float('inf') for node in graph}
prev = {node: None for node in graph}
# 시작 정점의 거리만 0으로 설정
d[start] = 0
# 최소 힙(우선순위 큐)에 (거리, 정점) 형태로 삽입
pq = []
heapq.heappush(pq, (0, start))
# 아직 방문하지 않은 정점들을 관리 -> (pq가 빌 때까지)
while pq:
# 현재 거리가 최소인 정점을 꺼냄
current_dist, u = heapq.heappop(pq)
# 이미 저장된 최단 거리보다 크면 무시(과거 정보)
if current_dist > d[u]:
continue
# u와 인접한 각 정점 v에 대해 거리 갱신 시도
for w, v in graph[u]: # (가중치, 인접정점)
if d[v] > d[u] + w:
d[v] = d[u] + w
prev[v] = u
# 거리 갱신되면 우선순위 큐에 새로 삽입
heapq.heappush(pq, (d[v], v))
return d, prev
if __name__ == "__main__":
# 예시 그래프 (인접 리스트)
# graph[u] = [(가중치, 인접정점), ...]
graph = {
1: [(2, 2), (4, 3)],
2: [(2, 1), (3, 3), (1, 4)],
3: [(4, 1), (3, 2), (5, 4)],
4: [(1, 2), (5, 3)]
}
start_node = 1
dist, prev = dijkstra(graph, start_node)
print(f"최단 거리 배열 (d[]) = {dist}")
print(f"선행 정점 배열 (prev[]) = {prev}")
# dist[v]를 통해 "start_node에서 v까지의 최단 거리" 확인 가능
# prev[v]를 이용하면 역추적하여 경로를 복원할 수 있음.
(1)
/ \
2 4
/ \
(2)---3---(3)
\ /
1 5
\ /
(4)
Python
복사
2.3. 성능 및 특징
•
시간 복잡도
◦
인접 행렬 O(|V|^2)
◦
인접 리스트 + 힙 O((|V| + |E|) log |V|)
•
음의 가중치를 갖는 간선이 없어야 함
3. 벨만-포드 알고리즘
3.1. 개념
•
정의
◦
단일 출발점 최단 경로를 찾는 알고리즘
•
특징
◦
음의 가중치를 갖는 간선을 포함한 그래프에서도 적용 가능.
▪
음의 사이클이 없는 경우에 한함
◦
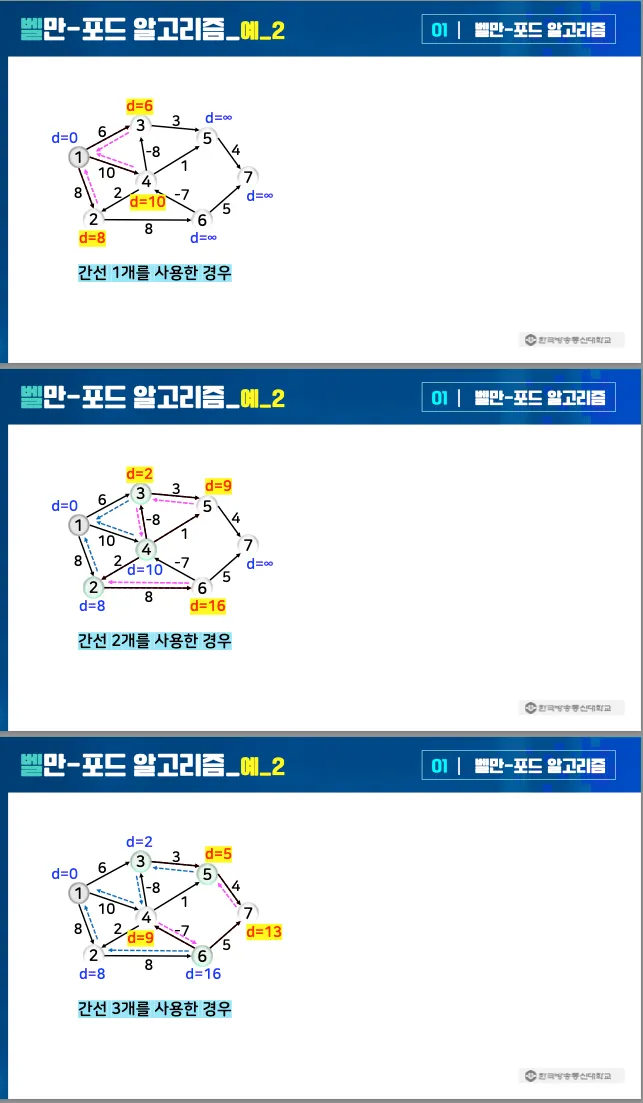
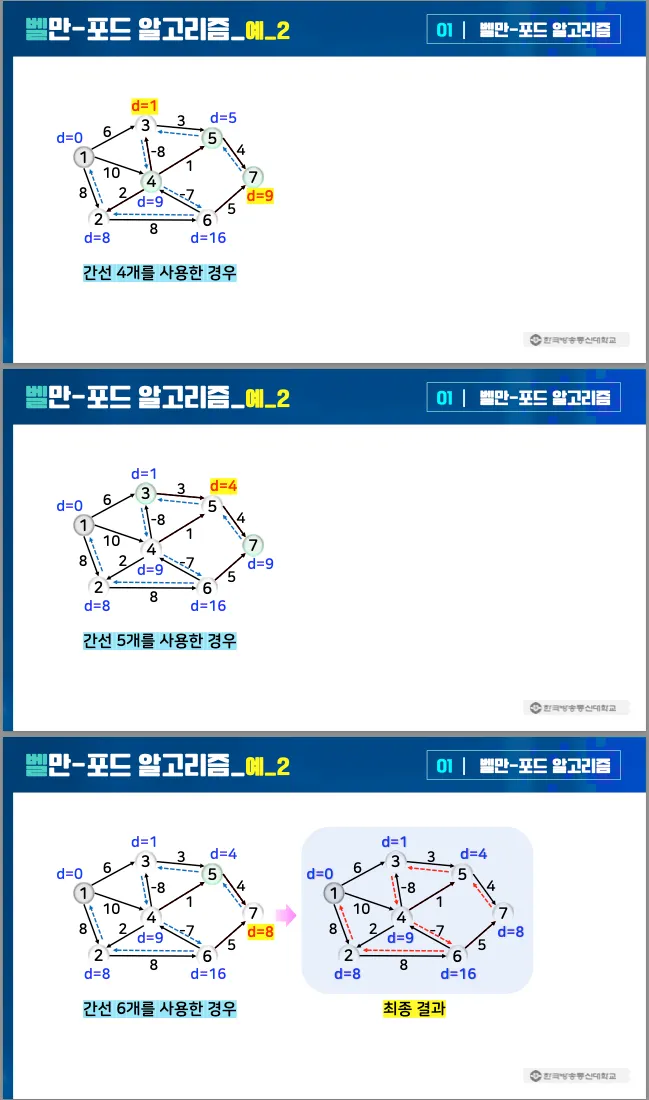
G = (V, E) 에서 |V| = n 일때 단계적으로 최단 경로를 구해나가는 방법
▪
단계적으로 간선 개수를 늘려가며 최단 경로를 계산
▪
최대 (n-1)개의 간선을 사용하는 최단 경로를 구함
•
동작 원리
◦
초기화:
▪
출발점 s의 거리를 0으로 설정 (d[s]=0).
▪
나머지 모든 정점의 거리는 ∞로 설정 (d[v]=∞).
1.
반복:
•
총 |V|-1번의 반복 과정에서 각 간선을 순회하며 거리값을 갱신
•
거리 갱신 식: d[v] = min(d[v], d[u] + w(u, v)).
2.
최종 거리 갱신
•
마지막 단계에서 거리값 조정이 발생한다면 음의 사이클 존재
•
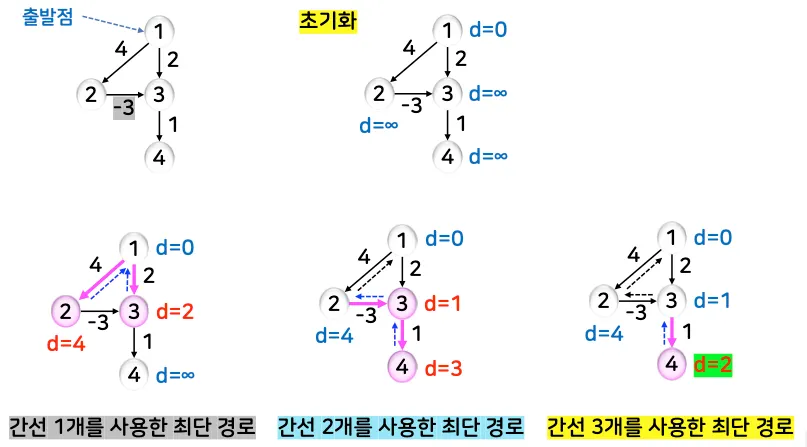
예시 1
•
예시 2
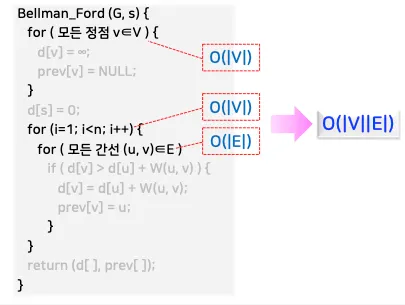
3.2. 예시 코드
Bellman_Ford(G, s) {
for ( 모든 정점 v ∈ V ) {
d[v] = ∞;
prev[v] = NULL;
}
d[s] = 0;
for ( i = 1; i < n; i++ ) {
for ( 모든 간선 (u, v) ∈ E )
if ( d[v] > d[u] + W(u, v) ) {
d[v] = d[u] + W(u, v);
prev[v] = u;
}
}
return ( d[], prev[] );
}
C
복사
def bellman_ford(V, E, s):
"""
벨만-포드 알고리즘 (단일 시작점 s 로부터의 최단 경로)
:param V: 정점들의 리스트 혹은 집합 (ex. [1,2,3,4,...])
:param E: 간선들의 리스트 (ex. [(u, v, w), (u2, v2, w2), ...])
:param s: 시작 정점
:return: (d, prev)
d[v] : s 로부터 v 까지의 최단 경로 거리
prev[v]: s -> ... -> v 최단 경로 상에서 v 바로 이전 정점
"""
# 1. 거리 배열 d, 이전 정점 배열 prev 초기화
d = {v: float('inf') for v in V}
prev = {v: None for v in V}
# 시작 정점 s의 거리는 0으로 설정
d[s] = 0
# 2. 모든 간선에 대해 (V-1)번 반복하여 거리 완화(Relaxation)
for _ in range(len(V) - 1):
for (u, v, w) in E:
# 현재 기록된 거리보다 u -> v를 거쳐 가는 경로가 더 짧다면 갱신
if d[u] != float('inf') and d[u] + w < d[v]:
d[v] = d[u] + w
prev[v] = u
# 3. 음수 사이클(Negative Cycle) 검사
# (추가로 원하는 경우, 음수 사이클 존재 여부 확인 가능)
for (u, v, w) in E:
# 더 갱신될 수 있다면, 음수 사이클 존재
if d[u] != float('inf') and d[u] + w < d[v]:
print("Error: 음수 사이클(Negative Cycle)이 존재합니다.")
# 필요 시 여기서 별도로 처리(예: 예외 발생, 사이클에 속한 정점 추적 등)
break
return d, prev
# 예시 실행
if __name__ == "__main__":
# 예: 정점이 1~5, 간선이 아래와 같다고 가정
V = [1, 2, 3, 4, 5]
E = [
(1, 2, 6),
(1, 3, 7),
(2, 4, 5),
(2, 3, 8),
(2, 5, -4),
(3, 4, -3),
(3, 5, 9),
(4, 2, -2),
(5, 1, 2),
(5, 4, 7)
]
s = 1 # 시작 정점
d, prev = bellman_ford(V, E, s)
print("최단 거리 d:", d)
print("이전 정점 prev:", prev)
Python
복사
3.3. 성능 및 특징
•
시간 복잡도
◦
최악의 경우: O(|V||E|) (모든 간선을 반복적으로 검사).
•
장점
◦
음의 가중치를 갖는 간선이 있는 경우에도 최단 경로를 계산할 수 있음
◦
모든 간선을 매번 조사하는 대신, 이전 단계에서 거리값이 조정된 정점에 연결된 간선만 조사하여 효율 개선 가능
•
특징
◦
음의 가중치를 갖는 간선이 있는 경우
▪
데이스크트라 알고리즘 적용 불가
▪
벨만-포드 알고리즘 적용 가능
•
단 음의 사이클이 존재하면 적용 불가
◦
음이 가중치를 갖는 간선이 없는 경우
▪
데이스크트라 알고리즘 → 바람직
▪
벨만-포드 알고리즘
4. 플로이드 알고리즘
4.1. 개념
•
정의
◦
모든 정점 쌍 간의 최단 경로를 찾는 알고리즘
•
특징
◦
동적 프로그래밍 기반의 알고리즘
◦
중간에 거쳐 갈 수 있는 정점을 하나씩 추가하면서 경로를 계산
◦
음의 가중치를 포함할 수 있지만, 음의 사이클이 존재하면 안 됨
•
수행 과정
1.
초기화
•
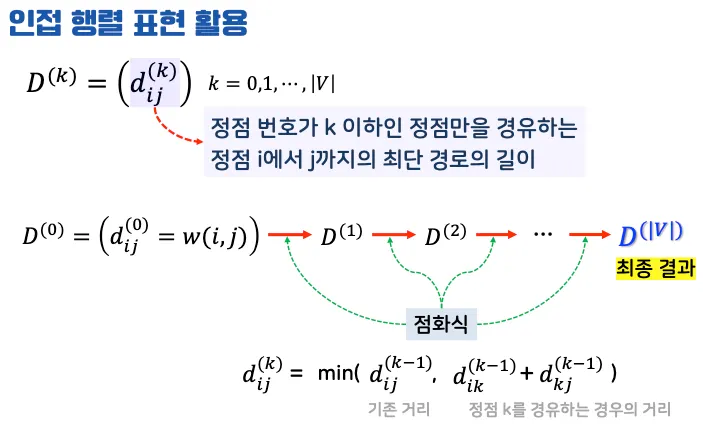
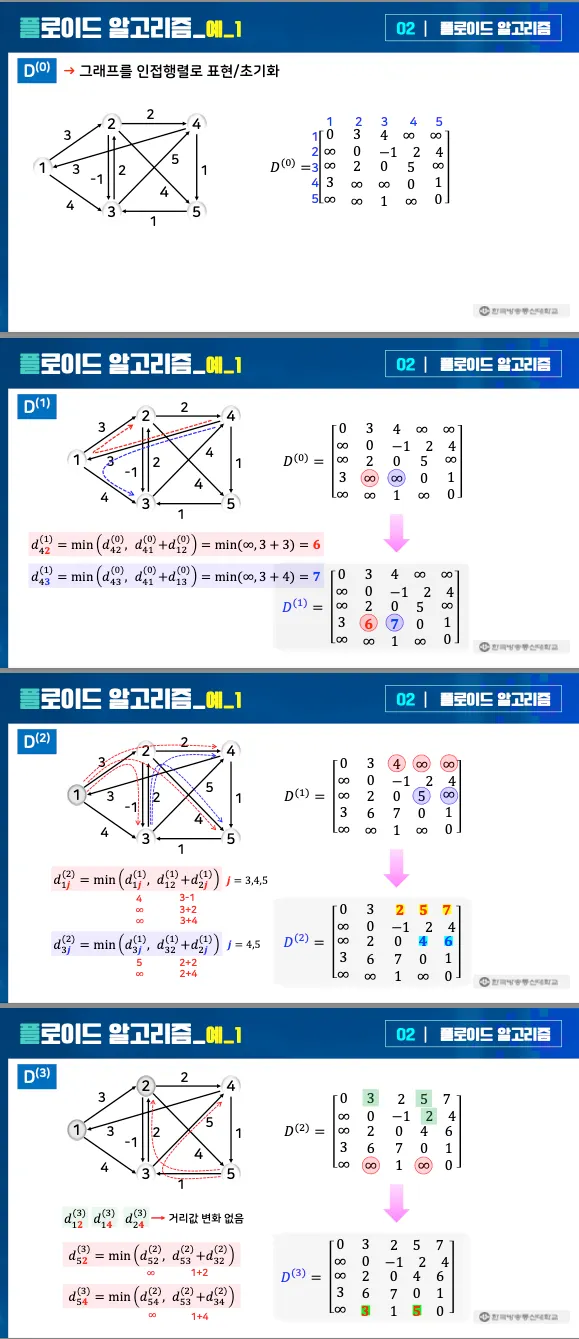
그래프를 인접 행렬로 표현: 초기 행렬 D[0]은 각 간선의 가중치를 나타냄.
•
없는 간선은 ∞, 자기 자신으로 가는 경로는 0.
2.
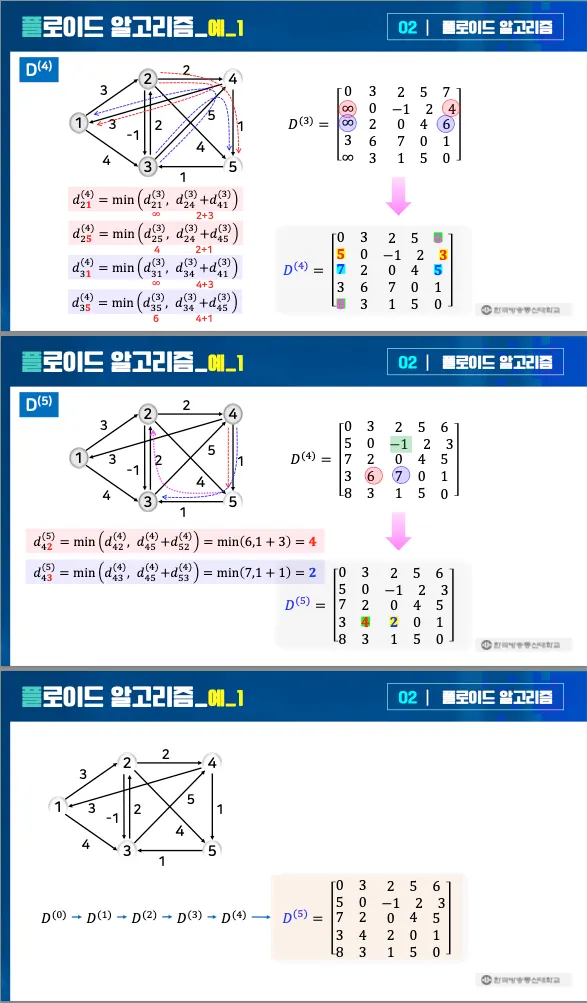
중간 정점 추가
•
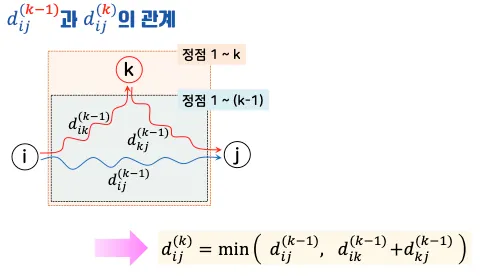
정점 k까지를 포함한 최단 경로 계산.
•
점화식: d[i][j] = min(d[i][j], d[i][k] + d[k][j]).
3.
최종 행렬 반환
•
최단 경로를 나타내는 최종 거리 행렬 D[n]
•
인접 행렬 표현 활용
•
예시
4.2. 예시 코드
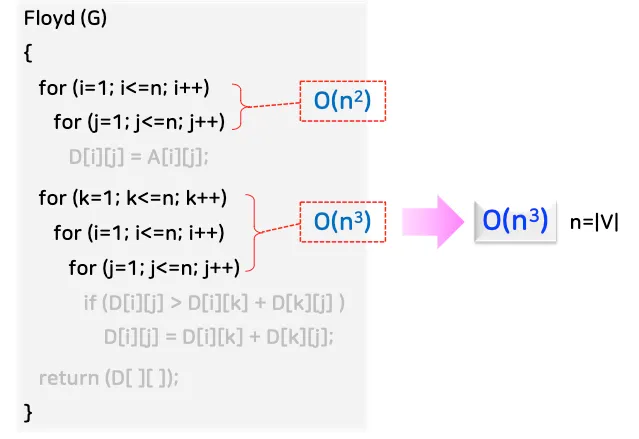
// 입력: G=(V,E), 인접 행렬 A[1..n][1..n]
// 출력: D[][] : 모든 정점 쌍 간의 최단 경로의 길이
Floyd (G)
{
// D^(0) = ( d_ij^(0) = w_ij )
for (i=1; i<=n; i++)
for (j=1; j<=n; j++)
D[i][j] = A[i][j];
// D^(k): 경유하는 정점 k
for (k=1; k<=n; k++)
for (i=1; i<=n; i++) // D_ij
for (j=1; j<=n; j++)
if (D[i][j] > D[i][k] + D[k][j]) // 경유하는 경우
D[i][j] = D[i][k] + D[k][j];
return (D[][]);
}
C
복사
def floyd_warshall(matrix):
"""
플로이드-워셜 알고리즘을 이용해 모든 정점 쌍 최단 경로를 구한다.
:param matrix: 그래프의 인접 행렬 (list of lists),
matrix[i][j]는 정점 i -> j 로의 가중치
:return: dist (list of lists), dist[i][j]는 i에서 j로 가는 최단 거리
"""
# 정점 개수 n
n = len(matrix)
# dist 배열을 초기 행렬(matrix)로 복사
dist = [row[:] for row in matrix]
# 모든 정점 k(경유지)에 대해
for k in range(n):
# 모든 출발점 i에 대해
for i in range(n):
# 모든 도착점 j에 대해
# 경유지 k를 거치는 경로가 기존보다 더 짧다면 갱신
if dist[i][j] > dist[i][k] + dist[k][j]:
dist[i][j] = dist[i][k] + dist[k][j]
return dist
# 예시 사용
if __name__ == "__main__":
import math
# 예시: 4개의 정점(0,1,2,3)이 있다고 가정
# 초기 인접 행렬 (가중치)
# ∞는 math.inf 로 표현
matrix = [
[0, 5, math.inf, 10],
[math.inf, 0, 3, math.inf],
[math.inf, math.inf, 0, 1],
[math.inf, math.inf, math.inf, 0]
]
dist_result = floyd_warshall(matrix)
print("플로이드 알고리즘 결과 (모든 쌍 최단 거리):")
for row in dist_result:
print(row)
Python
복사
4.3. 성능 및 특징
•
시간복잡도
◦
최악의 경우 O(n^3)
•
특징
◦
동적 프로그래밍 방법을 적용한 알고리즘
◦
데이크스트라 알고리즘으로 모든 쌍 최단 경로를 구할 수있음
▪
각 정점에 대해서 반복적으로 적용해서 해결 가능
▪
플로이드 알고리즘이 더 간단하므로 빠르게 수행
◦
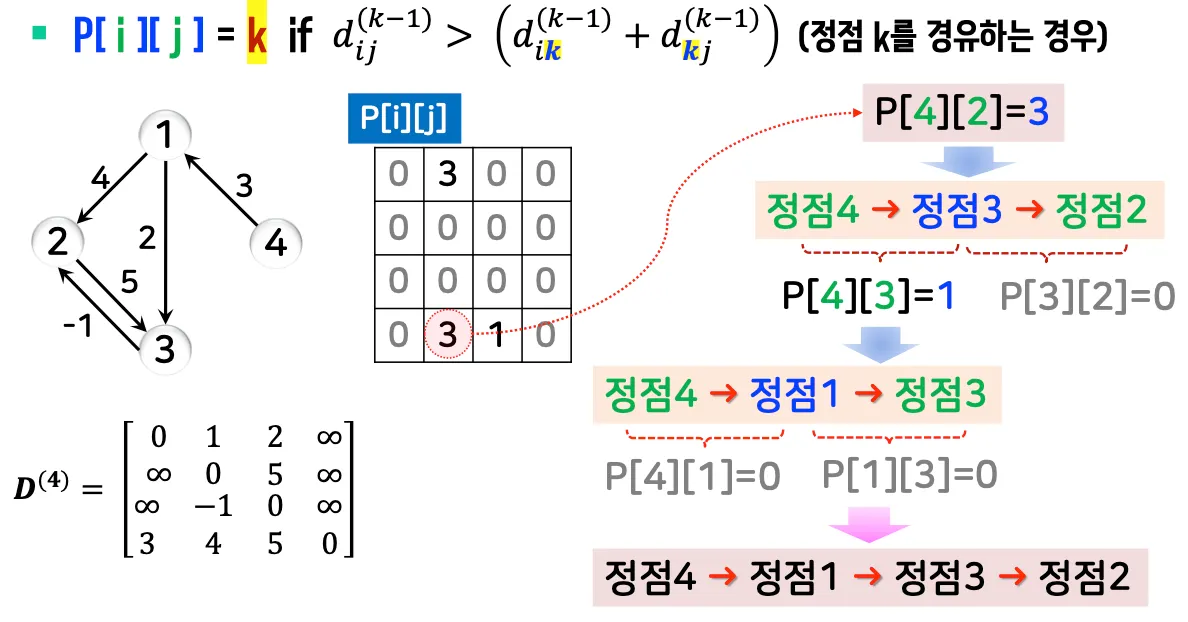
P[1..n][1..n]을 활용하면 최단 경로 자체를 구할 수 있음
3. 포드-풀커슨 알고리즘
3.1. 네트워크 플로 문제
•
주어진 네트워크에 대해서 플로를 최대로 하는 값을 찾는 문제
◦
소스에서 싱크로 보낼 수 있는 플로 값을 최대로 하는 문제 → ”최대 플로 문제”
•
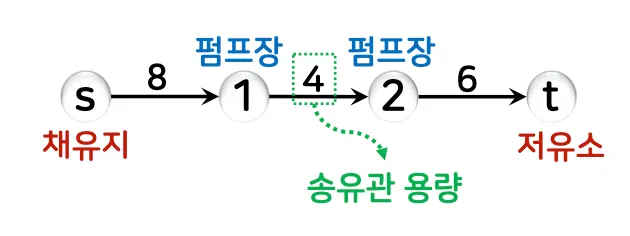
네트워크 N = (V, E, s, t, c)
◦
방향 그래프 G=(V, E)
◦
s → 소스 (시작점, 진입차수가 0인 정점)
◦
t → 싱크 (도착점, 진출차수가 0인 정점)
◦
c → 간선의 가중치 → 간선의 용량 (capacity)
▪
c(u, v) → 간선 <u, v>를 통해 보낼 수 있는 최대의 양/값
3.2. 포드-풀커슨 알고리즘 개요
•
목적: 네트워크 플로 문제에서 최대 플로 값을 찾는 방법
•
특징:
◦
증가 경로(augmenting path)를 반복적으로 찾아 플로를 증가시킴
◦
순방향 간선과 역방향 간선을 고려
◦
간선의 용량이 정수일 경우에는 종료 보장이 됨
3.3. 수행 과정
1.
초기화
•
모든 간선의 플로를 0으로 설정
2.
증가 경로 탐색
•
소스에서 싱크까지의 증가 경로를 탐색
•
증가 경로의 잔여 용량 계산: ∆ = min(r(u, v) for 모든 간선)
3.
플로 갱신
•
순방향 간선: f(u, v) += ∆
•
역방향 간선: f(u, v) -= ∆
4.
종료 조건
•
더 이상 증가 경로가 존재하지 않을 때 알고리즘 종료
3.4. 잔여 용량과 증가 경로
•
잔여 용량: r(u, v) = c(u, v) - f(u, v) (순방향 간선)
•
역방향 간선: r(v, u) = f(u, v) (간선 용량 감소 가능)
3.5. 성능
•
시간 복잡도: O(|E|F), 여기서 F는 최대 플로 값
•
개선 알고리즘: 에드몬즈-카프 알고리즘(BFS 사용)은 O(|V||E|²)
3.6. 제약 조건 및 응용
•
간선 용량이 무리수일 경우 종료 보장 없음
•
응용 사례:
◦
물류 네트워크 최적화
◦
전송 네트워크에서 최대 데이터 전송량 계산