Total
Search
1. 힙 정렬
1.1. (최대) 힙이란?
•
정의
◦
각 노드의 값이 자신의 자식 노드의 값보다 크거나 같은 완전 이진트리
•
장점
◦
임의의 값 삽입과 최댓값 삭제가 쉬움
•
구현
◦
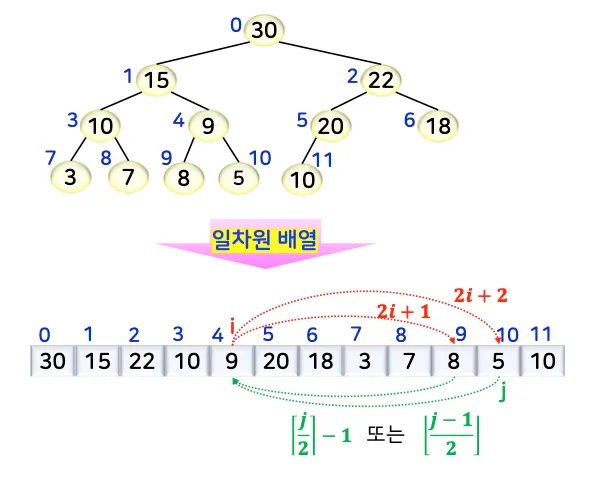
일차원 배열로 구현 가능 → 간단한 인덱스 계산을 통해 부모/자식 노드에 대한 용이한 접근
1.2. 힙 정렬의 개념과 처리 과정
힙 자료구조를 이용한 정렬 알고리즘
1.
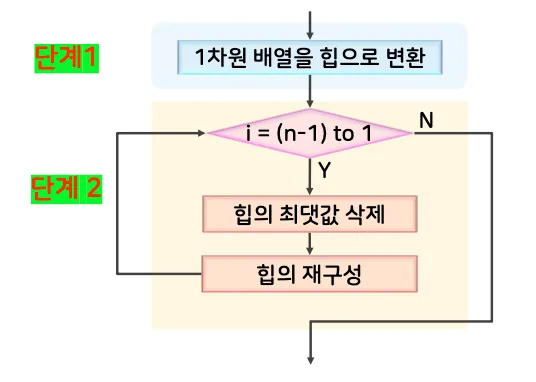
단계 1: 주어진 일차원 배열을 초기 힙으로 구축
2.
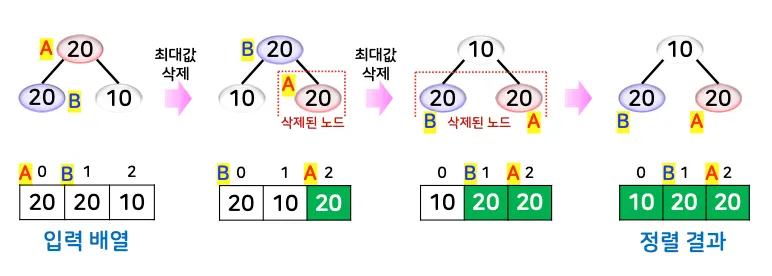
단계 2: 최댓값 삭제 및 힙으로 재구성하는 과정을 반복
•
힙의 루트 노드(최댓값)와 힙의 마지막 노드 값을 교환
•
교환한 루트 노드를 리프 노드 방향으로 내려가며 힙 조건을 만족하도록 재정비
•
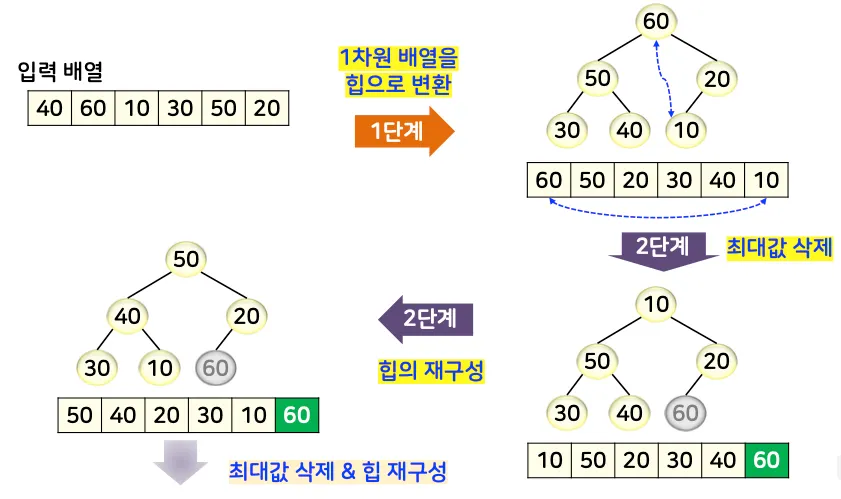
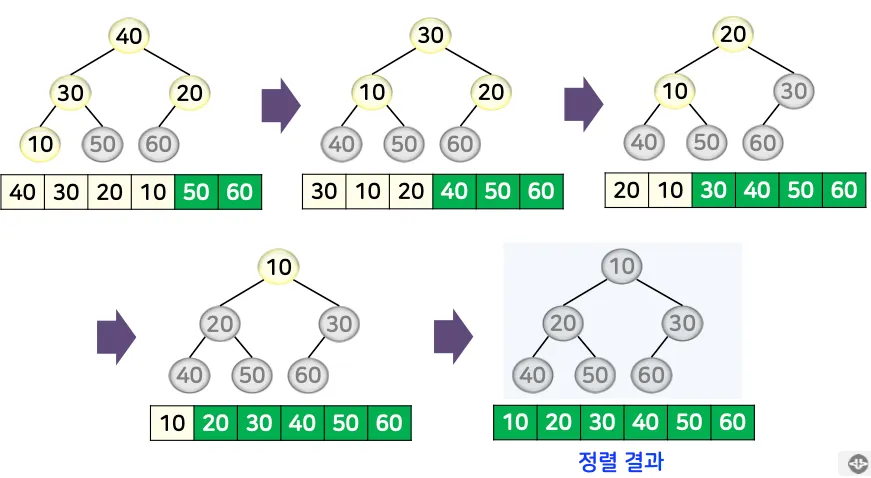
처리 과정
1.3. 힙 정렬 알고리즘
#include <stdio.h>
// A 배열을 힙 정렬하는 함수
void heapSort(int A[], int n) {
int i, par, cur, lch, rch, tmp;
// 단계 1: 0번 인덱스부터 차례대로 삽입하며 '상향식'으로 최대 힙 구성
for (i = 0; i < n; i++) {
par = (i / 2) - 1; // 부모 노드 인덱스 계산
while (par >= 0 && A[par] < A[i]) {
// 부모보다 새로 삽입된 노드가 더 크면 교환
tmp = A[par];
A[par] = A[i];
A[i] = tmp;
// 한 레벨 위로 이동해 다시 비교
i = par;
par = (i - 1) / 2;
}
}
// 단계 2: 최대값(루트)과 마지막 노드를 교환 후, 재구성 반복
for (i = n - 1; i > 0; i--) {
// A[0] (힙의 최대값)과 A[i] (현재 힙의 마지막 원소) 교환
tmp = A[0];
A[0] = A[i];
A[i] = tmp;
// 교환 후, 0번 인덱스부터 힙 재구성
cur = 0;
lch = 1;
rch = 2;
// 힙 재구성 과정
do {
// 오른쪽 자식이 존재하고, 왼쪽 자식보다 더 크면 왼쪽 자식을 rch로 갱신
if (rch < i && A[lch] < A[rch]) {
lch = rch;
}
// 더 큰 자식과 현재 노드를 비교해 교환
if (lch < i && A[lch] > A[cur]) {
tmp = A[cur];
A[cur] = A[lch];
A[lch] = tmp;
cur = lch;
lch = cur * 2 + 1;
rch = cur * 2 + 2;
}
else {
// 더 이상 재구성할 곳이 없으면 종료
lch = i;
}
} while (lch < i);
}
}
// 테스트용 main
int main() {
int A[] = {3, 1, 9, 7, 4, 10, 2};
int n = sizeof(A) / sizeof(A[0]);
heapSort(A, n);
printf("정렬 결과: ");
for (int i = 0; i < n; i++) {
printf("%d ", A[i]);
}
printf("\n");
return 0;
}
C
복사
def heap_sort(A):
n = len(A)
# 단계 1: 0번 인덱스부터 차례대로 삽입하며 '상향식'으로 최대 힙 구성
i = 0
while i < n:
par = (i // 2) - 1 # 부모 인덱스
while par >= 0 and A[par] < A[i]:
# 부모보다 새로 삽입된 노드가 더 크면 교환
A[par], A[i] = A[i], A[par]
i = par
par = (i - 1) // 2
i += 1
# 단계 2: 최대값(루트)과 마지막 원소를 교환 후, 힙 재구성 반복
for i in range(n - 1, 0, -1):
# A[0] (힙의 최대값)과 A[i] (현재 힙의 마지막 원소) 교환
A[0], A[i] = A[i], A[0]
# 교환 후, 0번 인덱스부터 힙 재구성
cur = 0
lch = 1
rch = 2
while True:
# 오른쪽 자식이 있고, 왼쪽 자식보다 값이 크다면 lch를 오른쪽 자식으로
if rch < i and A[lch] < A[rch]:
lch = rch
# 더 큰 자식과 현재 노드를 비교 후 교환
if lch < i and A[lch] > A[cur]:
A[cur], A[lch] = A[lch], A[cur]
cur = lch
lch = 2 * cur + 1
rch = 2 * cur + 2
else:
break # 재구성이 끝나면 종료
# 테스트 예시
if __name__ == "__main__":
arr = [3, 1, 9, 7, 4, 10, 2]
heap_sort(arr)
print("정렬 결과:", arr)
Python
복사
1.3. 초기 힙 구축
1.
1차원 입력 배열을 힙으로 변환하는 것
•
두 가지 접근 방법
1.
삽입 반복 방식: 입력 배열의 각 원소에 대해 힙 삽입 과정을 반복
2.
하향식 방식: 입력 배열을 완전 이진트리로 만든 뒤, 아래에서 위, 오른쪽에서 왼쪽으로 진행하면서 힙 조건을 만족하도록 조정
2.
최댓값 삭제 및 힙으로 재구성하는 과정을 반복
1.4. 시간 복잡도 및 특성
•
최선, 최악, 평균 시간 복잡도: O(nlogn)
◦
초기 힙 생성, 최댓값 삭제 및 힙 재구성
▪
바깥 루프 → 입력 크기 n에 비례
▪
안쪽 루프 → 완전 이진 트리의 높이 logn에 비례
•
안정성: 불안정적 정렬
•
추가 공간 필요 여부: 제자리 정렬 (in-place)
2. 계수 정렬
2.1. 개념
•
데이터 분포 정보를 활용하는 정렬 알고리즘 (계수 정렬, 기수 정렬, 버킷 정렬)
•
정렬 원리
◦
주어진 데이터 중에서 자신보다 작거나 같은 값을 갖는 데이터의 개수를 계산하여 정렬할 위치를 찾아 정렬하는 방식
•
입력 값이 어떤 작은 정수 범위 내에 있다는 것을 알고 있는 경우에 적용 가능
•
k보다 작거나 같은 값을 갖는 데이터의 개수
→ 정렬 순서 상의 k의 마지막 위치
•
자신보다 작거나 같은 값을 갖는 데이터의 개수의 효율적인 계산 방법
◦
입력값의 범위 a~b에 해당하는 크기의 배열 COUNT[a..b]를 할당하고, 주어진 값들을 한 번 쭉 훑으면 각 입력값의 출현횟수의 누적값 계산이 가능
2.2. 동작 방식
1.
입력값 범위만큼 배열을 할당
2.
각 입력값에 대한 출현 횟수 기록
3.
출현 횟수의 누적합 계산
4.
입력 배열을 뒤에서부터 순회하면서, 각 값이 정렬 후에 위치할 인덱스를 누적합으로 확인하여 직접 배치
2.3. 예시 코드
def counting_sort(A):
"""
A: 정렬 대상 리스트 (0-based)
return: 정렬된 새 리스트 B (0-based)
"""
# 1. A의 최솟값(MIN)과 최댓값(MAX) 찾기
MIN = min(A)
MAX = max(A)
# 2. (MIN..MAX)에 해당하는 COUNT 배열 준비
range_ = MAX - MIN + 1
COUNT = [0] * range_
# 3. 각 원소에 대한 출현 횟수 세기
for value in A:
COUNT[value - MIN] += 1
# 4. COUNT 배열에서 누적합 구하기
for i in range(1, range_):
COUNT[i] += COUNT[i - 1]
# 5. 결과를 담을 배열 B
n = len(A)
B = [0] * n
# 6. A를 뒤에서부터 읽어 B에 배치
# COUNT[value - MIN]가 B 내에서의 위치
for i in range(n - 1, -1, -1):
value = A[i]
COUNT[value - MIN] -= 1
B[COUNT[value - MIN]] = value
return B
# 사용 예시
if __name__ == "__main__":
arr = [4, 1, 3, 2, 10, 7, 2]
sorted_arr = counting_sort(arr)
print("정렬 결과:", sorted_arr)
Python
복사
2.4. 시간 복잡도 및 특성
•
전제 조건: 입력값의 범위가 데이터의 개수보다 작거나 비례 → O(n)
•
안정성: 안정적 정렬
•
추가 공간 필요 여부: 제자리 정렬이 아님(별도의 배열 필요)
•
보편성: 범위가 큰 경우 메모리 낭비가 큼
3. 기수 정렬
3.1. 개념
•
데이터 분포 기반의 정렬 알고리즘
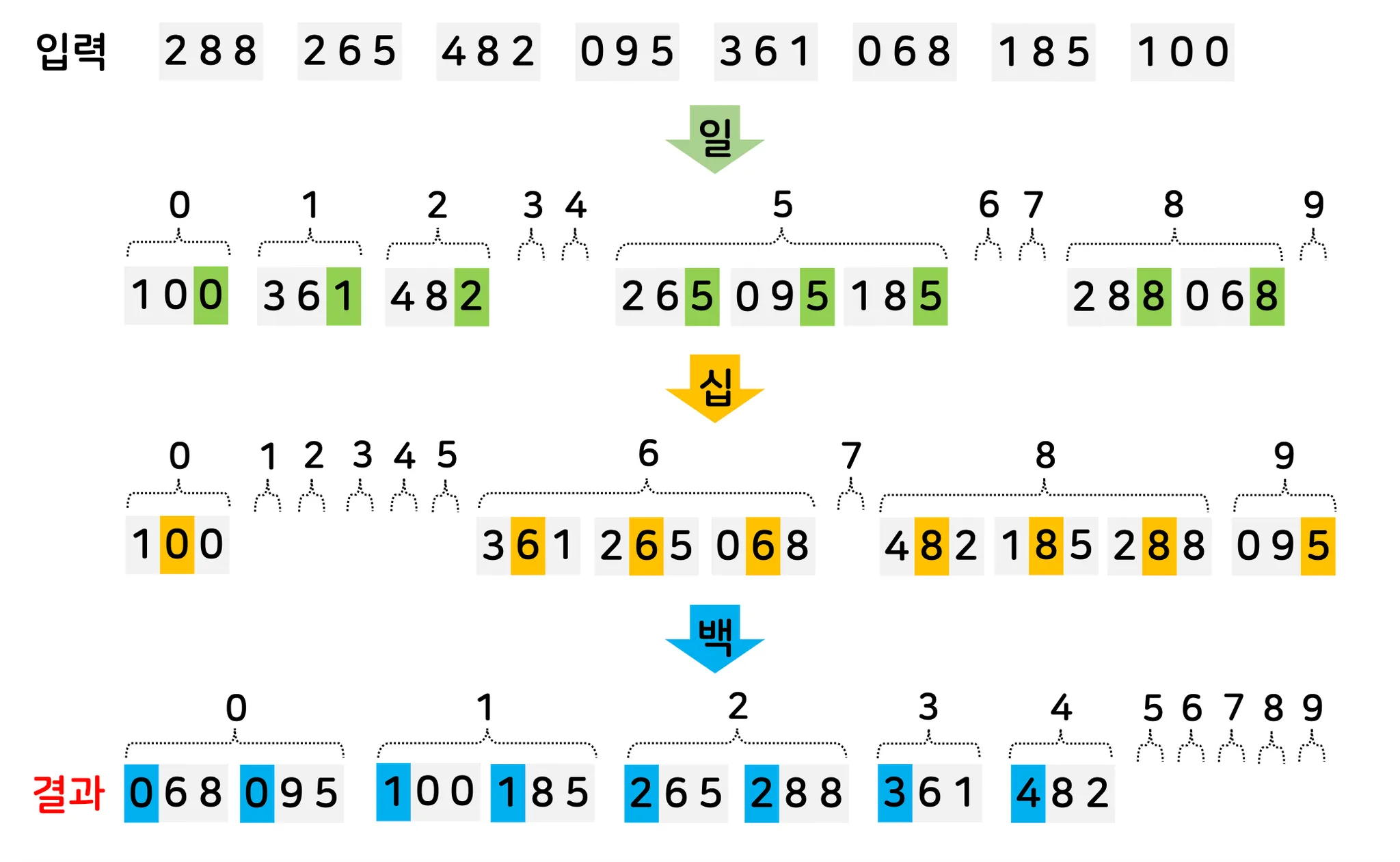
3.2. 정렬 원리
1.
주어진 데이터의 값을 자릿수(또는 특정 기준) 로 나눔
2.
각 자릿수에 대해 계수 정렬(또는 안정적인 정렬 알고리즘)을 적용
3.
자릿수를 낮은 자리수부터 높은 자리수까지 진행하며 정렬
3.3. 시간 복잡도 및 특성
•
전제 조건: 입력 데이터 자릿수가 상수일 때 → O(n)
•
안정성: 안정적 정렬
•
추가 공간 필요 여부: 제자리 정렬이 아님
3.4. 예시 코드
def counting_sort_by_digit(arr, exp):
"""
arr : 정렬할 리스트
exp : 현재 정렬하려는 자릿수를 나타내는 10^k (k=0,1,2,...)
"""
n = len(arr)
output = [0] * n # 현재 자릿수를 기준으로 정렬된 결과를 임시 보관할 리스트
count = [0] * 10 # 0~9까지 카운팅(계수) 배열
# 1) 각 원소의 해당 자릿수( (arr[i]//exp) % 10 )를 세어서 count에 기록
for i in range(n):
digit = (arr[i] // exp) % 10
count[digit] += 1
# 2) 누적 합을 구해서, 각 숫자가 output에서 차지할 인덱스 구간을 알아낸다
for i in range(1, 10):
count[i] += count[i-1]
# 3) arr를 뒤에서부터 순회하며(안정 정렬 유지), output에 올바른 위치로 삽입
for i in reversed(range(n)):
digit = (arr[i] // exp) % 10
output[count[digit] - 1] = arr[i]
count[digit] -= 1
# 4) output 배열을 다시 arr에 복사
for i in range(n):
arr[i] = output[i]
def radix_sort(arr):
"""
LSD 기수 정렬 함수
"""
# arr 내 최댓값을 찾아서, 그 자릿수만큼 반복
max_val = max(arr)
# exp: 1 -> 10 -> 100 -> ... 식으로 올라가며 각 자릿수를 정렬
exp = 1
while max_val // exp > 0:
counting_sort_by_digit(arr, exp)
exp *= 10
# 테스트 코드
if __name__ == "__main__":
arr = [170, 45, 75, 90, 802, 24, 2, 66]
print("정렬 전:", arr)
radix_sort(arr)
print("정렬 후:", arr)
Python
복사
4. 버킷 정렬
4.1. 개념
•
데이터 분포 기반의 정렬 알고리즘
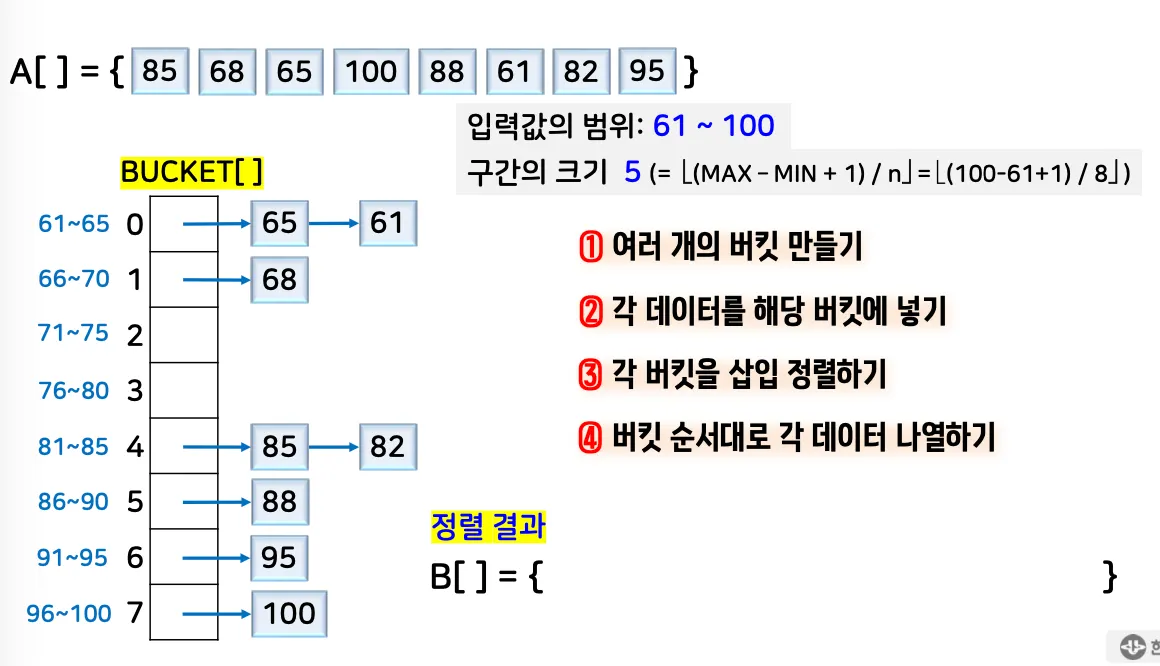
•
예시)
4.2. 정렬 원리
1.
데이터 값의 범위를 균등하게 n개의 버킷으로 분할
2.
각 데이터를 해당 버킷에 분류(Distribute)
3.
각 버킷 안에서 삽입 정렬(또는 다른 안정 정렬)을 수행
4.
버킷 순서대로 나열하여 결과 배열을 얻음
4.3. 시간 복잡도 및 특성
•
전제 조건: 데이터가 균등 분포이고, 버킷의 개수가 입력의 개수에 비례 → O(n)
•
안정성: 안정적 정렬
•
추가 공간 필요 여부: 제자리 정렬이 아님
4.4. 예시 코드
BucketSort(A[ ], n)
{
MIN = MAX = A[0];
for (i = 1; i < n; i++) { // 입력값 범위 MIN ~ MAX 계산
if (A[i] < MIN) MIN = A[i];
if (A[i] > MAX) MAX = A[i];
}
INTERVAL = ⌊(MAX - MIN + 1) / n⌋; // 버킷 구간의 크기 계산
for (i = 0; i < n; i++) { // 각 데이터를 해당 버킷에 넣기
A[i]를 BUCKET[ (A[i] - MIN) / INTERVAL ]에 삽입;
}
for (i = 0; i < n; i++) { // 버킷별로 정렬
삽입 정렬에 의해 BUCKET[i]를 정렬;
BUCKET[0], BUCKET[1], … 의 순서대로 데이터를 배열 B[ ]에 삽입;
}
return (B);
}
C
복사
def insertion_sort(bucket):
"""
버킷 안에 있는 원소들을 간단한 삽입 정렬로 정렬
"""
for i in range(1, len(bucket)):
key = bucket[i]
j = i - 1
while j >= 0 and bucket[j] > key:
bucket[j+1] = bucket[j]
j -= 1
bucket[j+1] = key
def bucket_sort(A):
n = len(A)
if n <= 1:
return A
# 1. MIN, MAX 찾기
MIN_val = min(A)
MAX_val = max(A)
# 2. 버킷 구간의 크기 계산
INTERVAL = (MAX_val - MIN_val + 1) // n
# 간단한 예외처리: INTERVAL이 0이 되지 않도록 조정
if INTERVAL == 0:
INTERVAL = 1
# 3. 버킷 리스트 생성 (필요한 개수만큼 생성)
buckets = [[] for _ in range(n)]
# 4. 각 데이터를 해당 버킷에 할당
for num in A:
# 버킷 인덱스 계산: (num - MIN_val) / INTERVAL
idx = (num - MIN_val) // INTERVAL
# 혹시 인덱스 범위를 벗어날 경우 마지막 버킷에 할당(오버플로 방지)
if idx >= n:
idx = n - 1
buckets[idx].append(num)
# 5. 각 버킷별로 정렬 (삽입 정렬 등)
for i in range(n):
insertion_sort(buckets[i])
# 6. 버킷들을 순서대로 합쳐서 결과 배열 B를 구성
B = []
for i in range(n):
B.extend(buckets[i])
return B
# 테스트 코드
if __name__ == "__main__":
arr = [34, 2, 121, 57, 18, 95, 77, 46, 3, 89]
print("정렬 전:", arr)
sorted_arr = bucket_sort(arr)
print("정렬 후:", sorted_arr)
Python
복사