Total
Search
1. 퀵 정렬(Quick Sort)
1.1. 개념
•
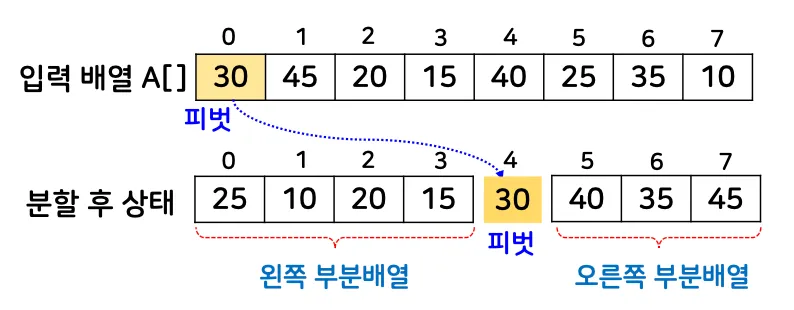
피벗을 기준으로 주어진 배열을 2개의 부분배열로 분할하고, 각 부분배열에 대해 퀵 정렬을 재귀적으로 수행하는 정렬 방식
•
분할 단계에서 피벗이 자신의 정렬된 위치(제자리)를 찾도록 하여 정렬을 진행
◦
왼쪽 부분 배열의 모든 값 < 피벗 < 오른쪽 부분 배열의 모든 값
•
피벗 (pviot: 분할 원소)
◦
주어진 배열을 두 부분배열로 분할하는 기준이 되는 특정 데이터
◦
보통 주어진 배열의 첫번째 데이터로 지정
1.2. 알고리즘
•
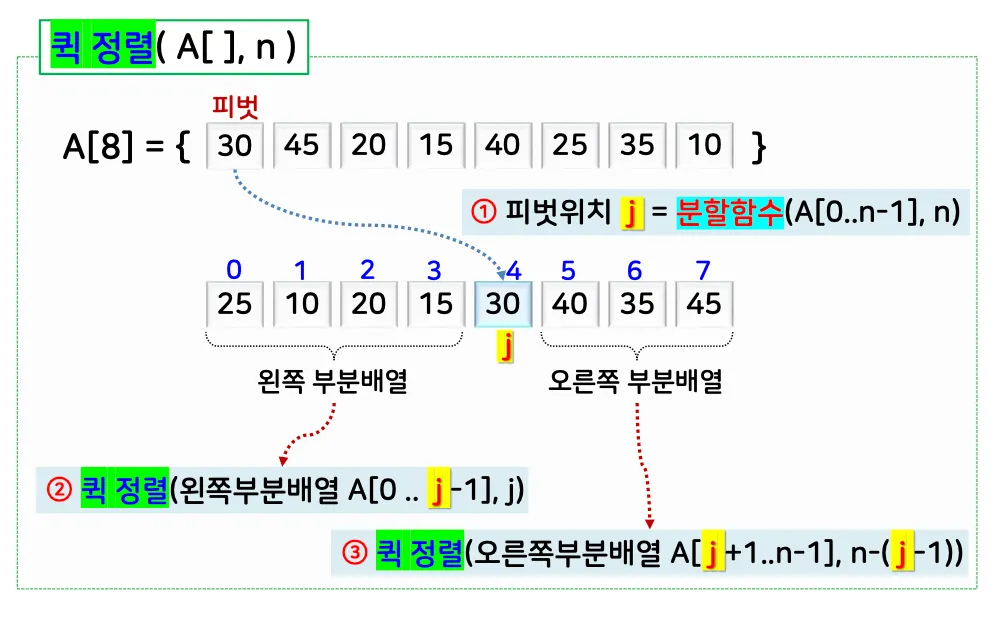
전체적인 처리 과정
•
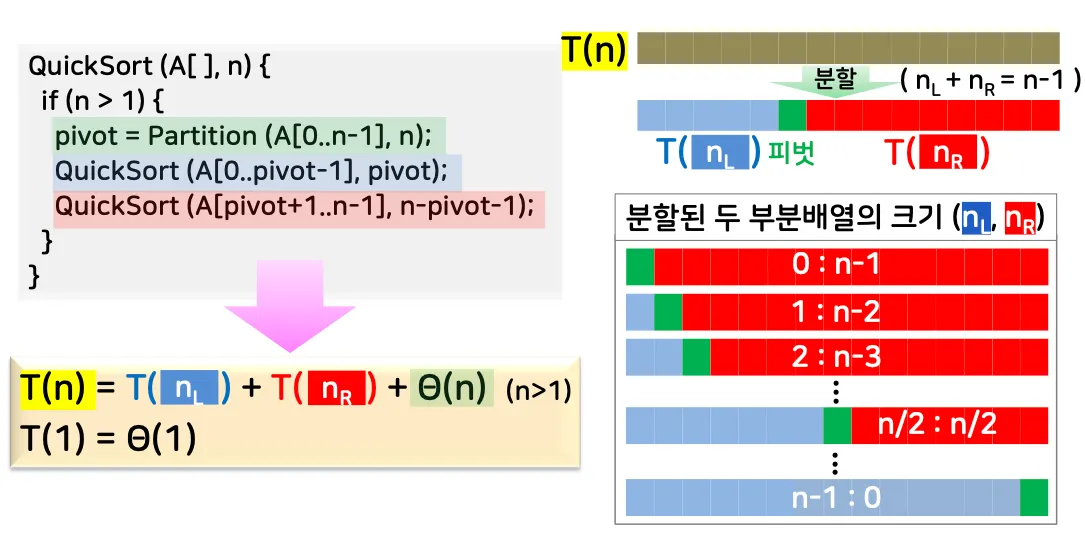
알고리즘
•
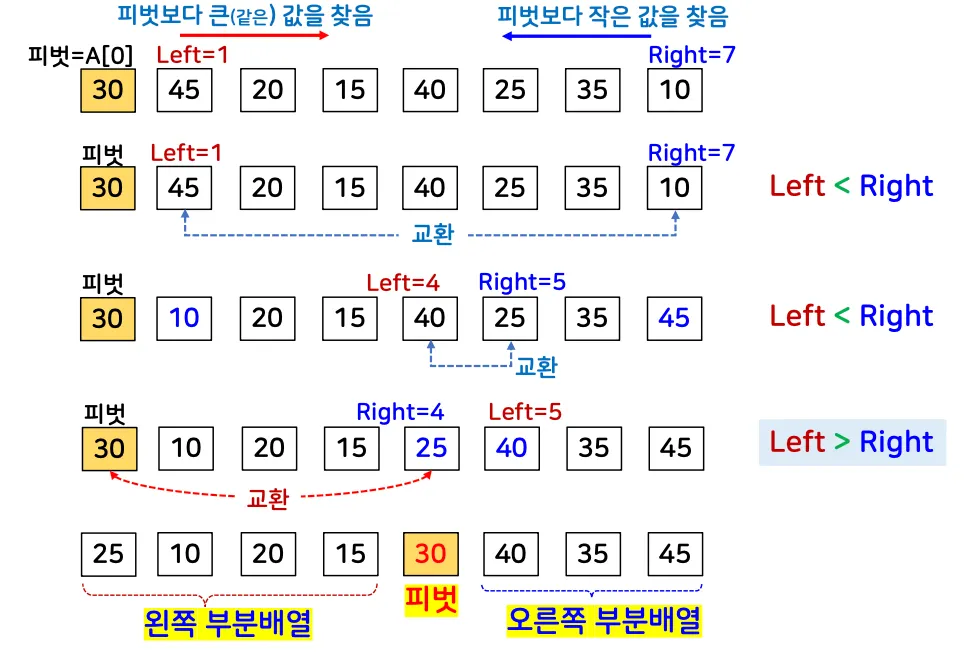
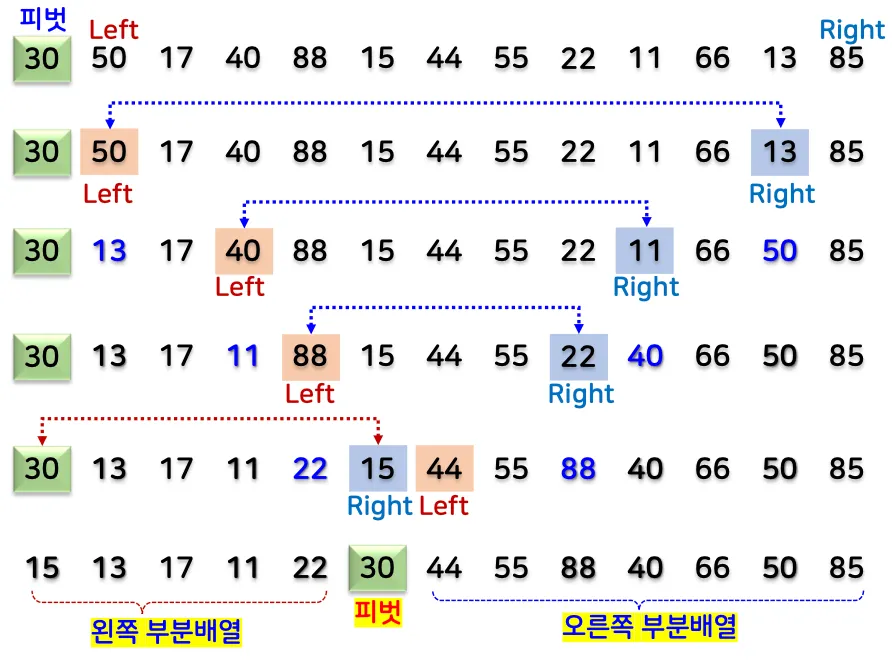
분할 과정
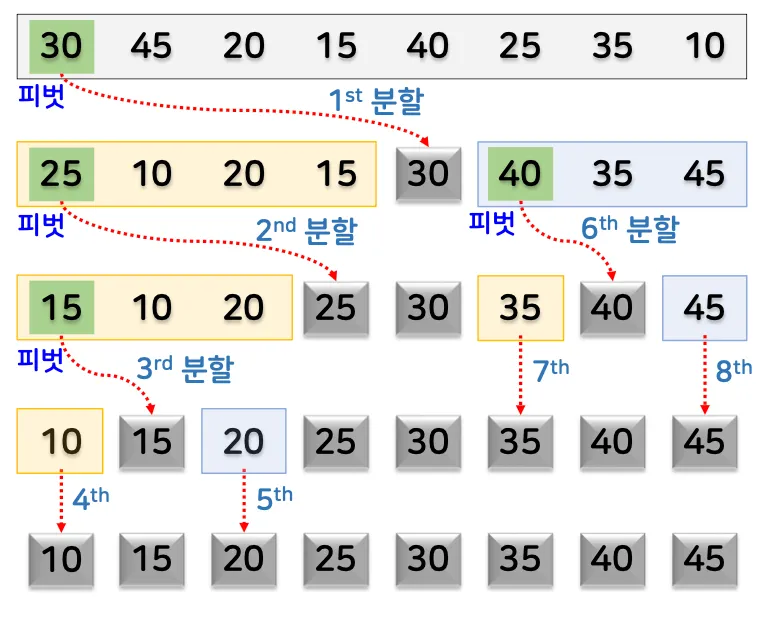
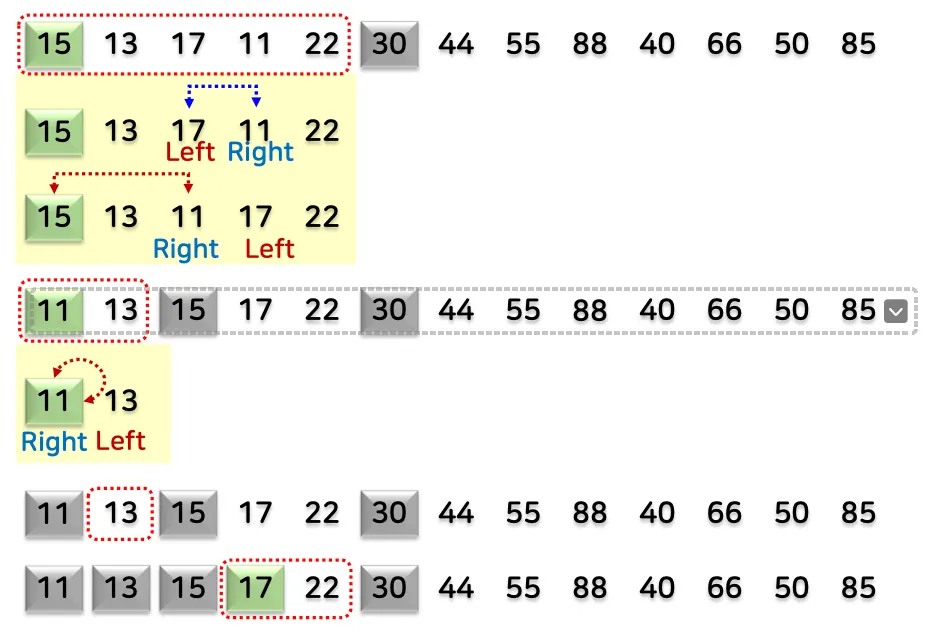
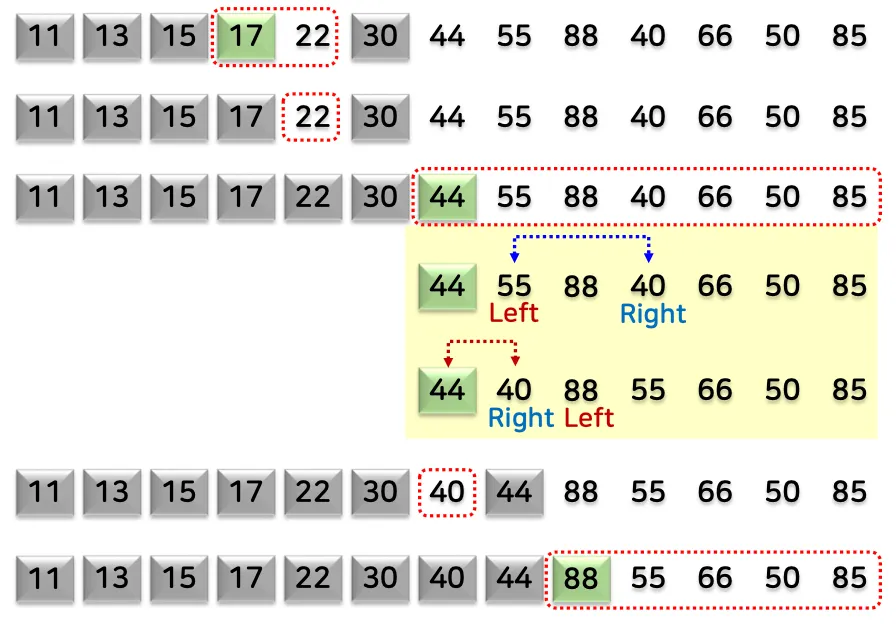
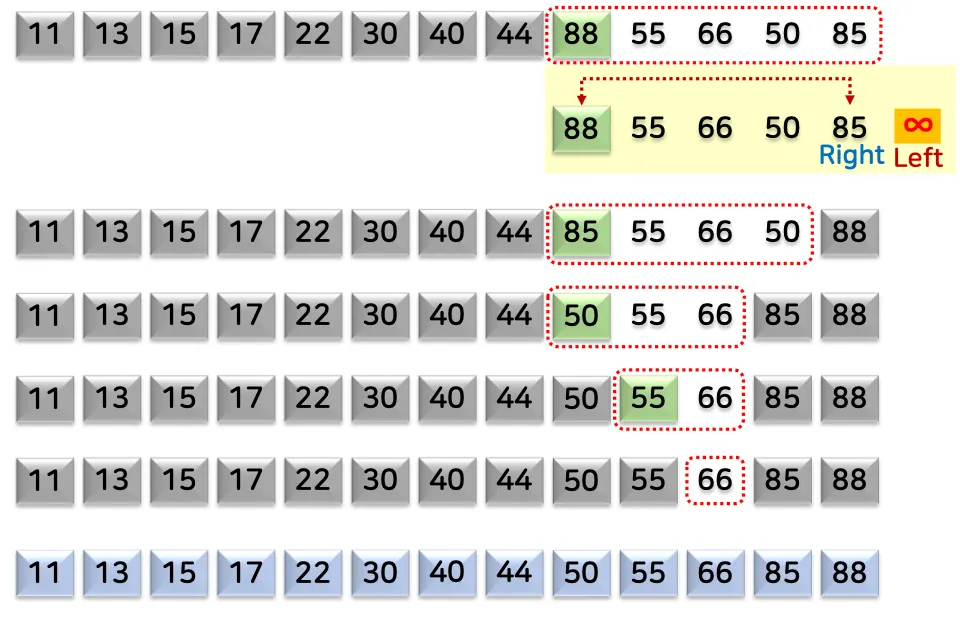
1.3. 예시
1.4. 성능 및 시간복잡도
•
분할 함수 Partition()의 성능 Θ(n)
◦
피벗과의 비교 횟수
◦
각 데이터는 피벗과 1회 또는 많아야 2회씩 비교
•
퀵 정렬 함수의 수행시간은 분할되는 두 부분 배열의 크기에 따라 달라짐
•
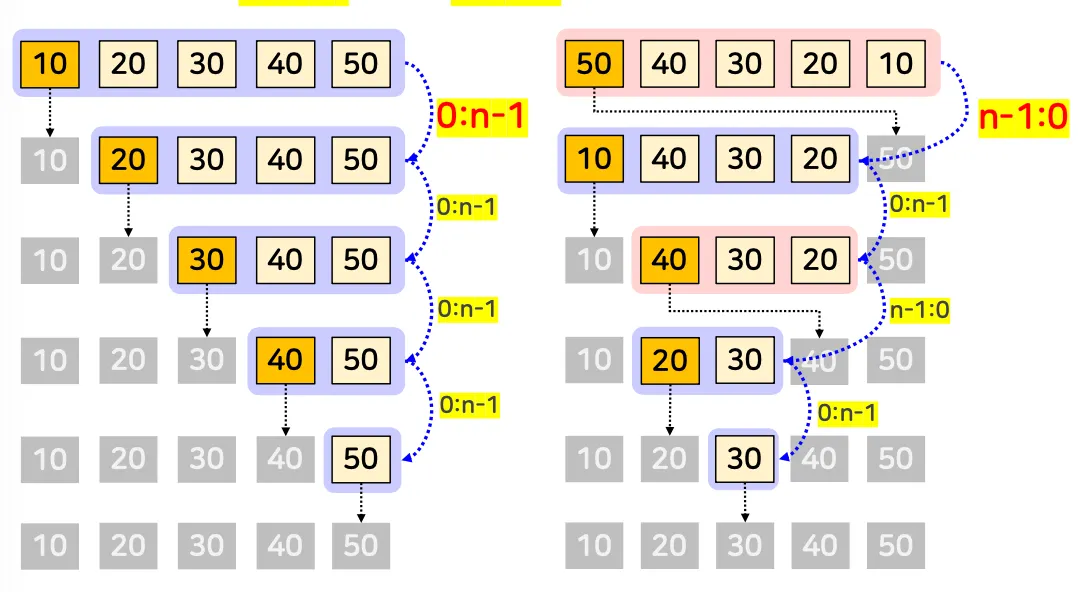
배열이 항상 0:n-1 또는 n-1:0으로 분할되는 경우 O(n²)
◦
극심한 불균형적 분할 (최악의 경우)
•
배열이 항상 n/2 : n/2으로 분할 되는 경우 O(nlogn)
◦
가장 균형적인 분할 (최선의 경우)
•
퀵 정렬의 평균 수행시간 O(nlogn)
1.5. 특징
•
피벗 선택의 임의성만 보장되면 평균 수행 시간 보장
◦
최선/평균 수행시간 O(nlogn)
◦
최악 수행시간 O(n²)
▪
조건
•
피벗을 배열의 첫번째 원소로 뽑고 배열이 정렬된 경우
▪
배열이 정렬되는지는 알 수 없음. 따라서 피벗을 배열의 첫번째 원소가 아닌 랜덤된 원소로 뽑으면 평균 수행시간을 보장할 수 있음
▪
배열에서 임의의 값을 선택한 후, 첫번째 원소와 서로 교환한 후 정렬 수행
•
불안정적 정렬
•
제자리 정렬
◦
분할 과정에서 주로 입력 배열 자체를 사용하고, 추가 메모리를 많이 사용하지 않음
•
분할정복 알고리즘이지만 결합(merge) 단계 없음
◦
분할 단계에서 이미 피벗이 제자리를 잡음
1.6. 예시 코드
QuickSort(A[], n) {
if (n > 1) {
// ① Partition 함수를 통해 피벗의 정렬 위치(pivotIndex) 찾기
int pivotIndex = Partition(A, n);
// ② 왼쪽 부분배열(피벗 기준 왼쪽)에 대한 퀵 정렬 재귀 호출
QuickSort(A, pivotIndex);
// ③ 오른쪽 부분배열(피벗 기준 오른쪽)에 대한 퀵 정렬 재귀 호출
QuickSort(A + pivotIndex + 1, n - pivotIndex - 1);
}
return;
}
// Partition 함수 (예시 구현)
Partition(A[], n) {
// 일반적으로 A[0] 또는 A[n-1], 혹은 임의 위치를 피벗으로 선택
int pivotValue = A[0];
int left = 1;
int right = n - 1;
while (left <= right) {
// pivotValue보다 큰 값이 나오기 전까지 left 이동
while (left <= right && A[left] <= pivotValue)
left++;
// pivotValue보다 작은 값이 나오기 전까지 right 이동
while (left <= right && A[right] > pivotValue)
right--;
if (left < right) {
// A[left]와 A[right] 교환
Swap(A[left], A[right]);
}
}
// pivotValue(맨 앞)와 A[right] 교환해 피벗의 위치 확정
Swap(A[0], A[right]);
return right; // 확정된 피벗 인덱스 반환
}
C
복사
def quick_sort(A, left, right):
if left < right:
# 분할(Partition) 후 피벗이 위치해야 할 인덱스 받기
pivotIndex = partition(A, left, right)
# 왼쪽 부분배열 퀵 정렬
quick_sort(A, left, pivotIndex - 1)
# 오른쪽 부분배열 퀵 정렬
quick_sort(A, pivotIndex + 1, right)
def partition(A, left, right):
pivotValue = A[left] # 맨 왼쪽 원소를 피벗으로 선택
l = left + 1
r = right
# l과 r이 교차하기 전까지 반복
while l <= r:
# pivotValue보다 작거나 같은 데이터를 찾을 때까지 l 증가
while l <= r and A[l] <= pivotValue:
l += 1
# pivotValue보다 큰 데이터를 찾을 때까지 r 감소
while l <= r and A[r] > pivotValue:
r -= 1
if l < r:
# 교차하지 않았다면 교환
A[l], A[r] = A[r], A[l]
# 교차 시점에서 피벗(A[left])을 A[r]과 교환 → 피벗 최종 위치 확정
A[left], A[r] = A[r], A[left]
return r # 확정된 피벗 인덱스 반환
# 사용 예시
if __name__ == "__main__":
A = [3, 6, 8, 10, 1, 2, 1]
quick_sort(A, 0, len(A) - 1)
print(A) # 정렬된 결과 출력
Python
복사
2. 합병 정렬(Merge Sort)
2.1. 개념
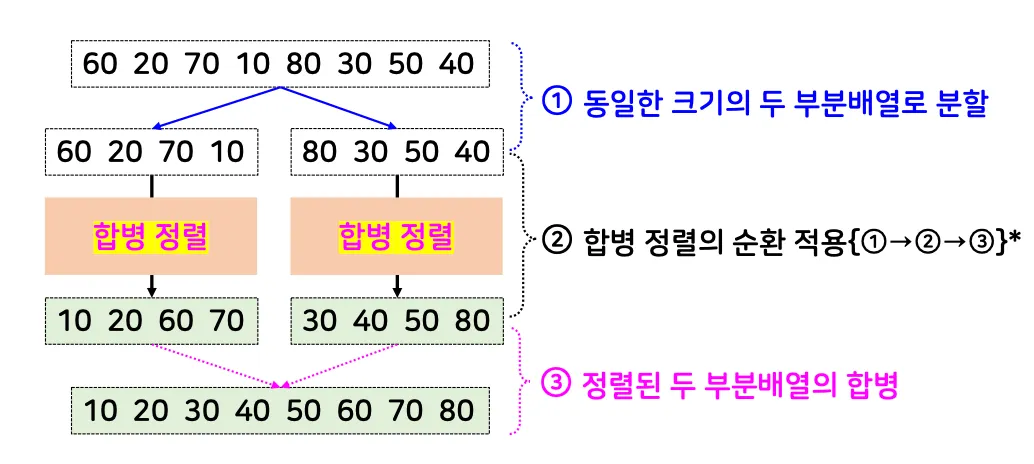
1.
주어진 배열을 동일한 크기의 2개 부분배열로 분할
2.
각 부분배열을 재귀적으로 합병 정렬 수행
3.
정렬된 두 부분배열을 합병(merge)하여 하나의 정렬된 배열로 만듦
2.2. 알고리즘
•
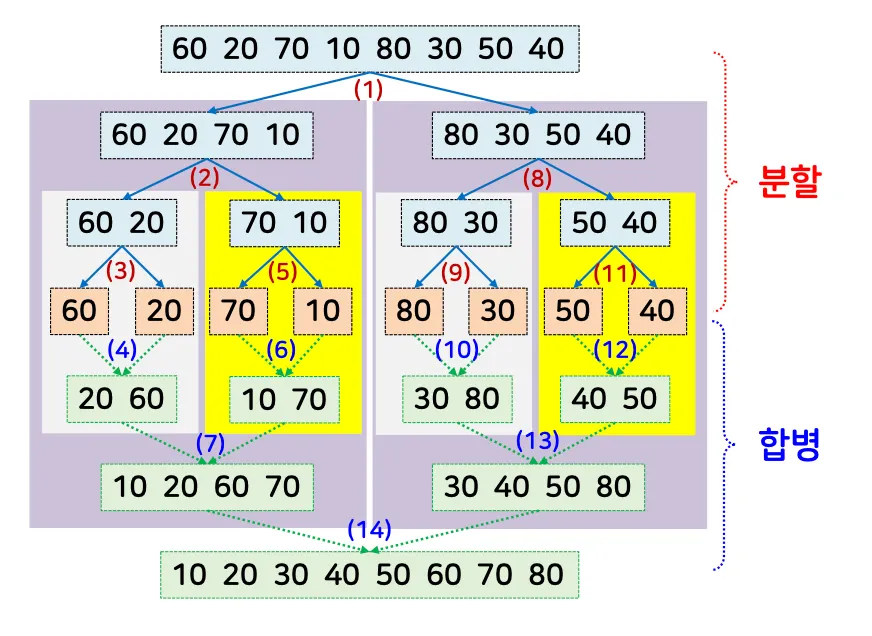
전체적인 수행 과정
•
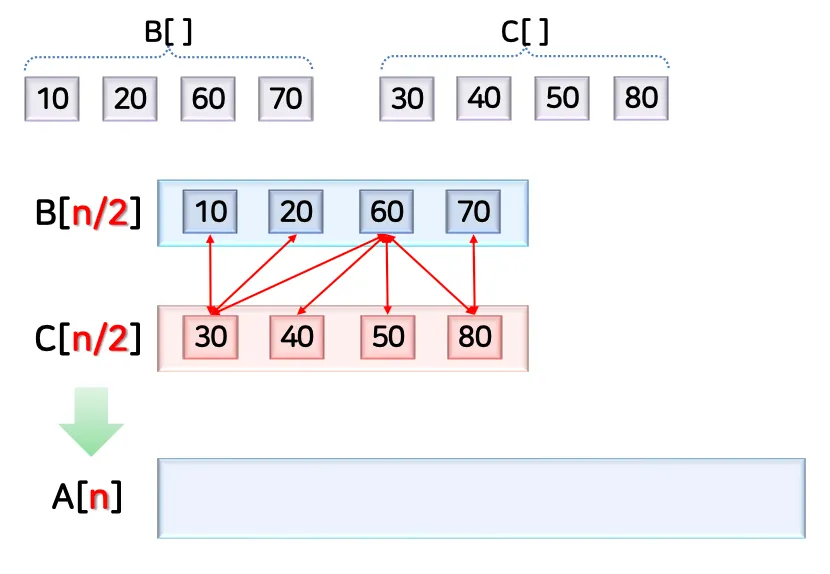
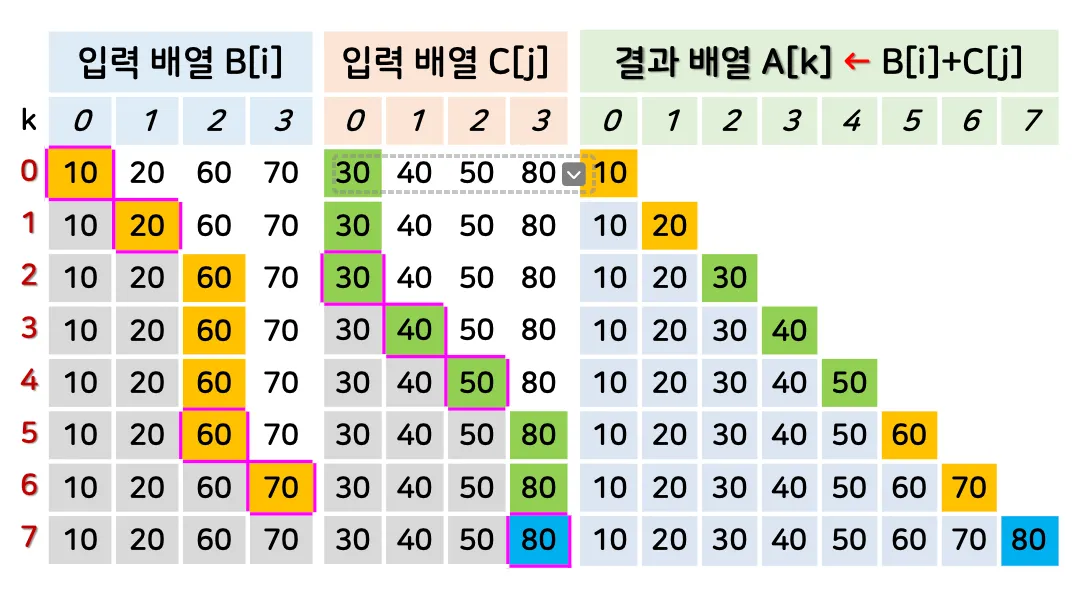
합병 변수 Merge()의 동작
2.3. 성능 및 시간 복잡도
•
합병 함수 Merge() 의 수행시간
◦
두 부분 배열의 비교 횟수 Θ(n)
•
합병 정렬 MergeSort()의 수행시간
•
최악 / 최선 평균: O(nlogn)
2.4. 특징
•
안정적인 정렬
◦
합병 과정에서 동일한 두 뎅터에 대해서 항상 왼쪽 데이터를 먼저 선택
•
제자리 정렬이 아님
◦
정렬된 두 부분배열을 결합하기 위해 전체 크기 n만큼의 추가 메모리가 필요
•
전형적인 분할정복 알고리즘
◦
분할 + 정복(재귀 정렬) + 합병 단계로 진행
2.5. 예시 코드
// Merge 함수를 통해 이미 정렬된 두 배열을 합쳐서 하나의 정렬된 배열을 만든다.
void Merge(int A[], int B[], int sizeB, int C[], int sizeC) {
int i = 0; // B 배열의 인덱스
int j = 0; // C 배열의 인덱스
int k = 0; // A 배열(결과)의 인덱스
// 두 배열(B, C)의 원소를 비교하며 작은 순으로 A에 복사
while (i < sizeB && j < sizeC) {
if (B[i] <= C[j]) {
A[k++] = B[i++];
} else {
A[k++] = C[j++];
}
}
// B 배열에 남은 원소가 있으면 A에 복사
while (i < sizeB) {
A[k++] = B[i++];
}
// C 배열에 남은 원소가 있으면 A에 복사
while (j < sizeC) {
A[k++] = C[j++];
}
}
void MergeSort(int A[], int n) {
if (n > 1) {
int Mid = n / 2;
// 왼쪽 부분배열 크기: Mid
// 오른쪽 부분배열 크기: n - Mid
// 임시 배열 B, C를 선언(혹은 동적 할당)하여 부분배열 복사
int *B = (int *)malloc(sizeof(int) * Mid);
int *C = (int *)malloc(sizeof(int) * (n - Mid));
// A의 앞부분[0..Mid-1]을 B로 복사
for (int i = 0; i < Mid; i++) {
B[i] = A[i];
}
// A의 뒷부분[Mid..n-1]을 C로 복사
for (int i = 0; i < (n - Mid); i++) {
C[i] = A[Mid + i];
}
// 재귀 호출: 왼쪽 부분배열 B와 오른쪽 부분배열 C 각각을 정렬
MergeSort(B, Mid);
MergeSort(C, n - Mid);
// 정렬된 B, C를 Merge하여 A[0..n-1]에 다시 저장
Merge(A, B, Mid, C, n - Mid);
// (선택) 동적 할당된 B, C 해제
free(B);
free(C);
}
}
C
복사
def merge_sort(A):
# 리스트 A를 재귀적으로 반씩 쪼개서 정렬 후 병합하여 반환
if len(A) <= 1:
return A
mid = len(A) // 2
left = merge_sort(A[:mid]) # 왼쪽 부분배열 재귀 정렬
right = merge_sort(A[mid:]) # 오른쪽 부분배열 재귀 정렬
return merge(left, right)
def merge(left, right):
# 이미 정렬된 두 리스트(left, right)를 합쳐서 하나의 정렬된 리스트를 반환
merged = []
i, j = 0, 0
while i < len(left) and j < len(right):
if left[i] <= right[j]:
merged.append(left[i])
i += 1
else:
merged.append(right[j])
j += 1
# 남은 원소들 처리
while i < len(left):
merged.append(left[i])
i += 1
while j < len(right):
merged.append(right[j])
j += 1
return merged
# 사용 예시
if __name__ == "__main__":
A = [3, 5, 1, 6, 2, 7, 4]
sorted_A = merge_sort(A)
print(sorted_A) # 정렬 결과 출력
Python
복사