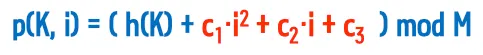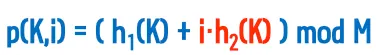Total
Search
1. 레드-블랙 트리
1.1. 개념
•
정의
◦
이진 탐색 트리의 구조를 기반으로 하되,
◦
균형성을 유지하기 위한 추가적인 성질을 만족하는 균형 탐색 트리
•
성질
1.
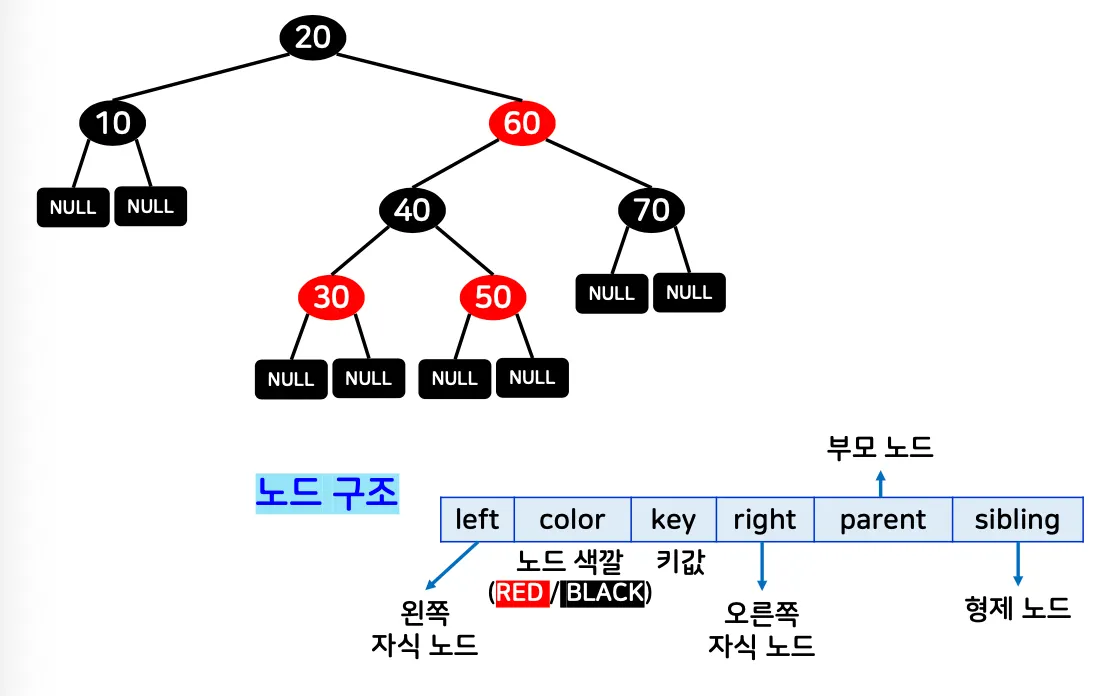
모든 노드는 검정 또는 빨강으로 표시
2.
루트 노드와 리프 노드는 항상 검정
•
모든 리프 노드는 NULL 노드로 간주
3.
빨강 노드의 부모는 항상 검정
•
빨강 노드가 연속으로 나타나지 않음
4.
임의의 노드에서 리프 노드까지의 경로에는 동일한 수의 검정 노드가 존재
5.
이진 탐색 트리의 성질을 모두 만족
•
예시
1.2. 연산
•
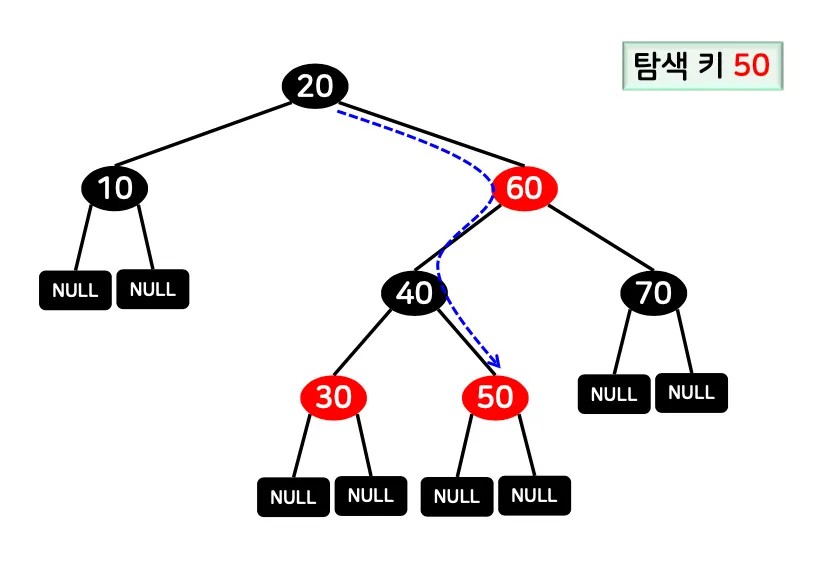
탐색 연산
◦
이진 탐색 트리의 방식과 동일. 루트에서 시작해 값의 크기에 따라 왼쪽/오른쪽으로 이동하며 탐색
•
삽입 연산
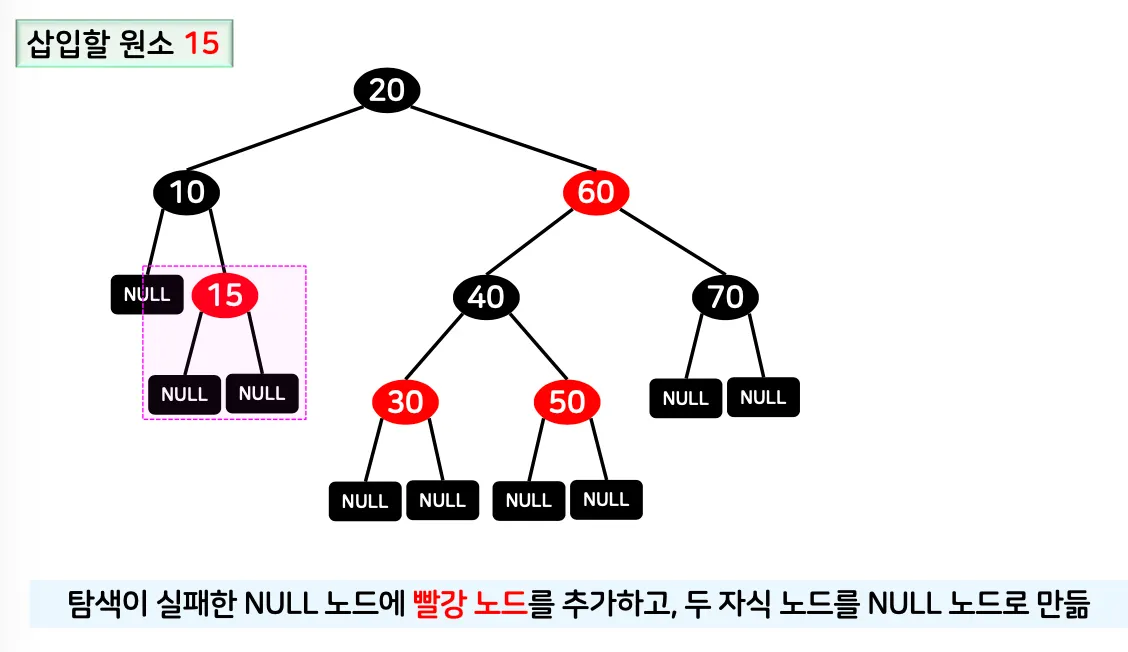
1.
탐색이 실패한 NULL 노드에 새로운 값을 빨강 노드로 추가
•
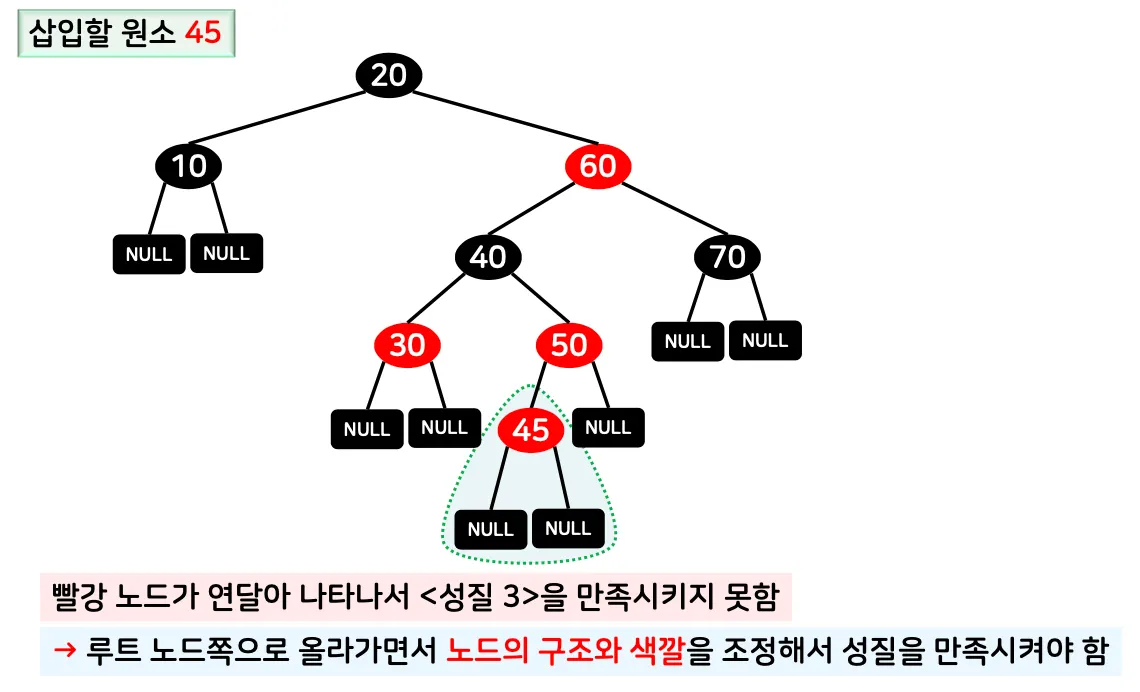
[삽입 연산 엣지]삽입 후 트리의 성질을 만족시키기 위해 추가 조정 필요
◦
빨강 노드가 연달아 나타나는 경우 노드의 구조 및 색깔을 조정
◦
이를 위해 다음 3가지 규칙 적용
▪
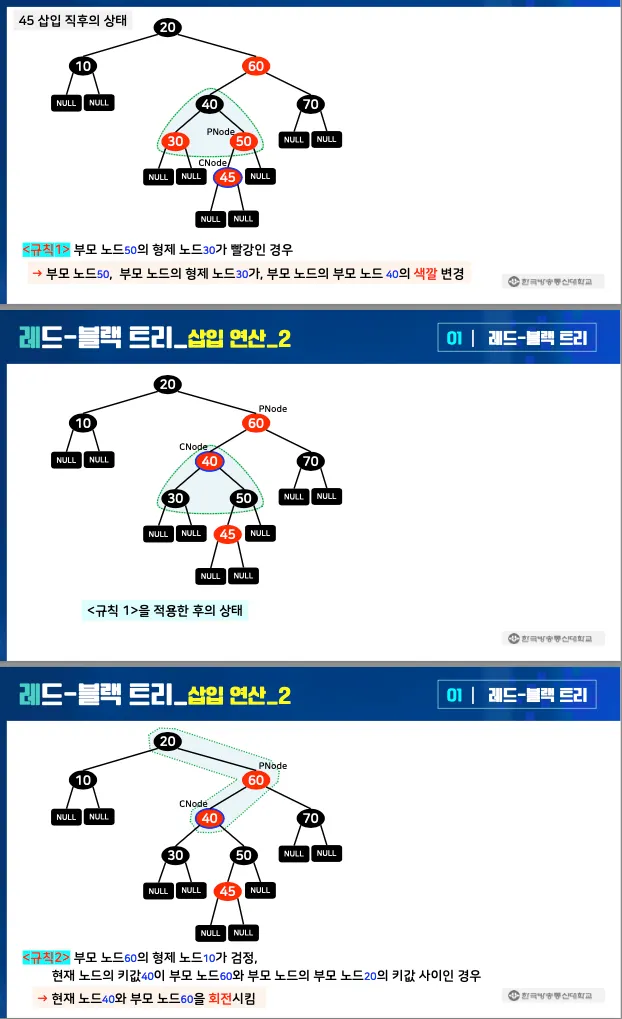
규칙 1: 부모 노드와 부모의 형제 노드가 빨강일 경우
•
부모 노드, 부모 노드의 형제 노드, 부모 노드의 부모 노드의 색깔을 모두 변경
▪
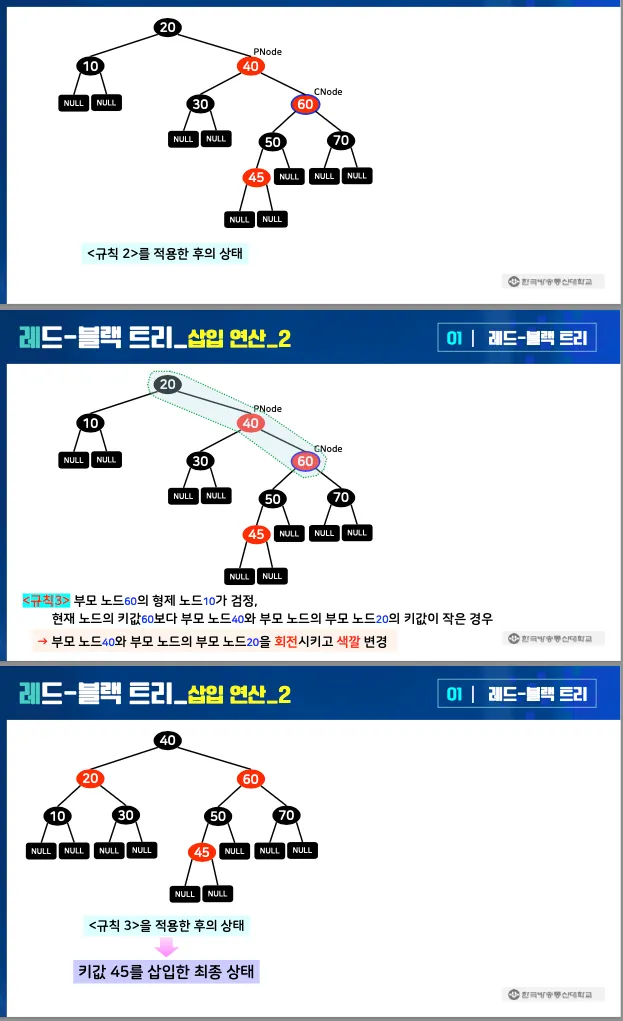
규칙 2: 부모 노드의 형제가 검정이고 현재 노드가 부모 노드와 부모 노드의 부모 노드의 키 값 사이인 경우
•
현재 노드와 부모 노드를 회전시킴
▪
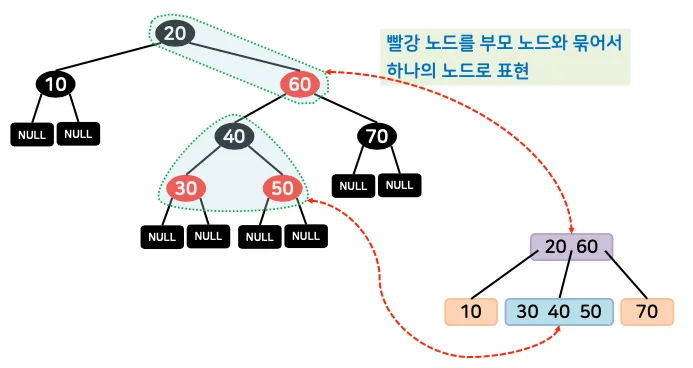
규칙 3: 부모 노드의 형제가 검정이고 현재 노드가 가장 큰(작은) 경우
•
부모 노드와 부모 노드의 부모 노드를 회전시키고 색깔을 변경
1.3. 성능과 특징
•
균형 탐색 트리
◦
어떤 두 리프 노드의 레벨 차이가 2배를 넘지 않는 균형 탐색 트리
▪
루트 노드에서 리프 노드의 경로상에는 빨강 노드 개수 < 검정 노드 개수
▪
루트 노드에서 리프 노드의 경로상에는 동일한 개수의 검정 노드가 존재
•
시간 복잡도: O(logn)
•
사실상 이진 탐색 트리
◦
탐색 연산은 이진 트리와 동일
◦
삽입 연산은 회전과 색깔 변경과 같은 추가 연산이 필요
◦
2-3-4 트리를 이진 탐색 트리로 변환한 형태
2. B-트리
2.1. 개념
•
정의
◦
다중 자식 노드를 허용하는 균형 이진 탐색 트리
◦
트리의 균형성을 보장하며 탐색, 삽입, 삭제의 효율성을 높임
•
성질 (t는 차수를 의미)
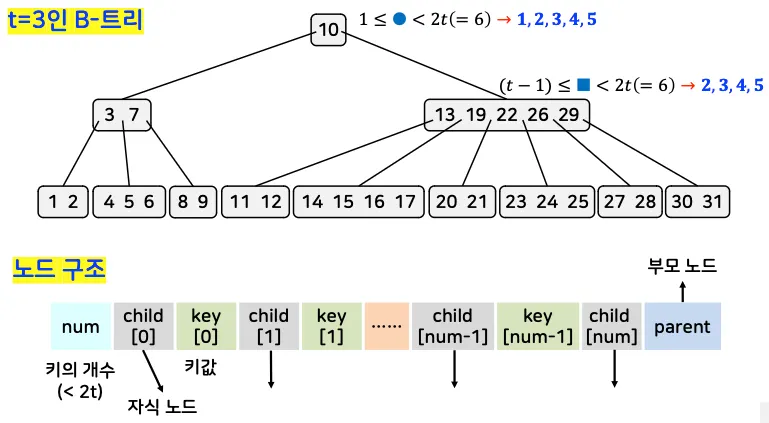
1.
루트 노드는 1개 이상, 2t개 미만의 오름차순으로 정렬된 키를 가짐
2.
루트 이외의 노드는 (t-1)개 이상 2t개 미만의 키를 가짐
3.
내부 노드는 자신이 가진 키의 개수보다 하나 더 많은 자식 노드를 가짐
4.
각 키의 왼쪽 서브트리에는 키보다 작은 값, 오른쪽 서브트리에는 키보다 큰 값이 위치
5.
모든 리프 노드는 동일한 레벨
•
예시
2.2. 연산
•
탐색 연산
◦
각 노드의 키를 확인하며 탐색
◦
키가 없는 경우 자식 노드로 이동
•
삽입 연산
◦
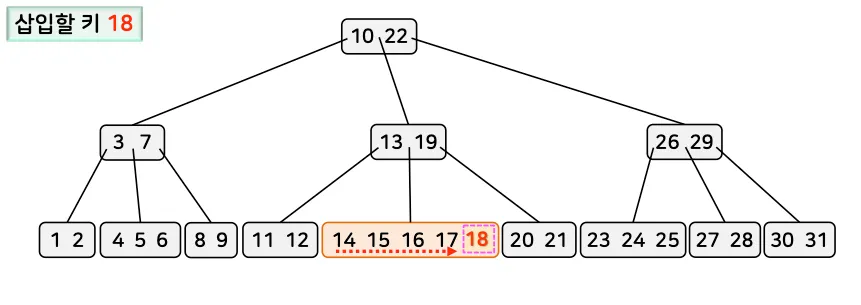
루트 노드에서부터 탐색을 수행하여 리프 노드에도 존재하지 않으면 해당 노드에 추가
◦
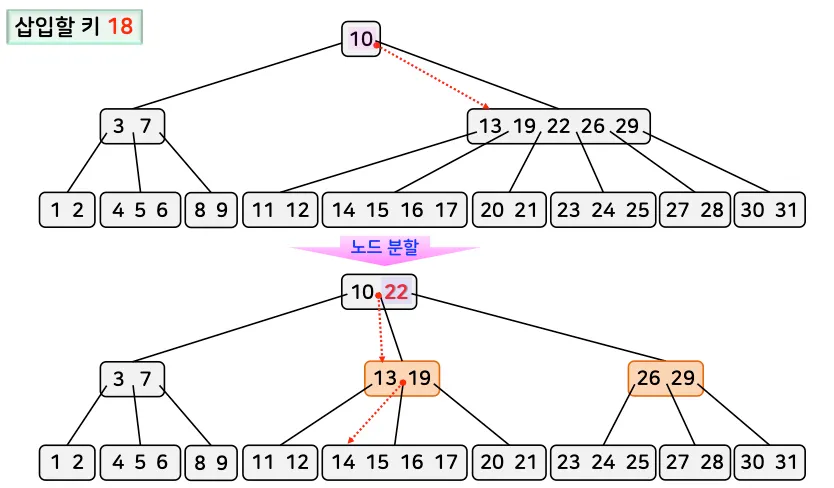
노드 분할
▪
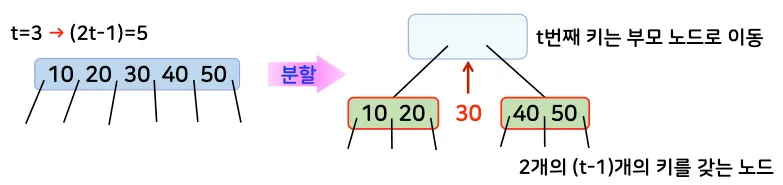
탐색 과정에서 (2t-1)개의 키를 갖는 노드를 만나면, 이 노드를 (t-1)개의 키를 갖는 2개의 노드와 1개의 키를 갖는 갖는 노드로 분할
▪
삽입으로 인해 노드의 키 개수가 2t개가 되는 것을 방지
•
노드 분할 예시
◦
t = 3
◦
2t-1 = 5
2.3. 성능
•
탐색, 삽입, 삭제 연산의 시간 복잡도 O(logn)
•
내부 탐색과 외부 탐색 모두에 활용
◦
내부 탐색
▪
t = 2 또는 t = 3 정도의 작은 값으로 지정
▪
t = 2 → 2-3-4 트리
▪
디스크 접근을 최소화하기 위해 사용
◦
외부 탐색
▪
디스크를 사용하는 경우라면 t를 충분히 크게 지정
•
한 노드의 크기가 디스크의 한 블록에 저장되도록 함
내부 탐색(Internal Search)
•
메인 메모리 안에서 자료구조로 사용되는 경우를 말합니다.
•
예를 들어, C++ STL의 std::set이나 std::map 등이 내부적으로 레드-블랙 트리(2-3-4 트리 변형)를 쓰는 것처럼, B-트리(또는 B+트리)의 변형을 사용하는 라이브러리도 있습니다.
•
내부 탐색에 사용한다면 메인 메모리 접근 속도를 고려하면 되고, 디스크 I/O를 크게 걱정할 필요는 없으니, t값을 작게(예: t=2나 t=3) 설정해도 좋습니다.
◦
예: 2-3-4 트리처럼, 키와 자식 수가 너무 많을 필요가 없습니다.
◦
메인 메모리는 접근 시간(랜덤 액세스)이 빠르므로, 트리 높이가 약간 커도 큰 문제가 되지 않습니다.
외부 탐색(External Search)
•
디스크나 SSD 등 외부 저장장치를 사용하는 경우를 말합니다.
•
데이터가 매우 크거나, 검색해야 할 자료가 많아서 모두 메인 메모리에 두기 어려운 상황에서 B-트리는 대표적인 선택지입니다.
•
이때는 디스크 블록(또는 페이지)의 크기에 맞춰서 한 노드가 가질 수 있는 키의 개수를 크게 잡습니다( t 값을 크게 설정).
◦
예: 디스크 블록 한 개가 4KB라면, 한 노드가 4KB를 꽉 채우도록 키와 자식 포인터를 배치하여 한 번 읽어올 때 최대한 많은 정보를 가져오도록 합니다.
◦
이렇게 하면 디스크 접근 횟수(블록 읽기 횟수)가 최소화되어, 전체 검색 성능이 크게 향상됩니다.
3. 해시 테이블
3.1. 개념
•
정의
◦
데이터를 저장, 삭제, 탐색할 때 키값을 해시 함수로 변환하여 주소 계산을 통해 상수 시간 내에 데이터 접근 가능
•
구성 요소
1.
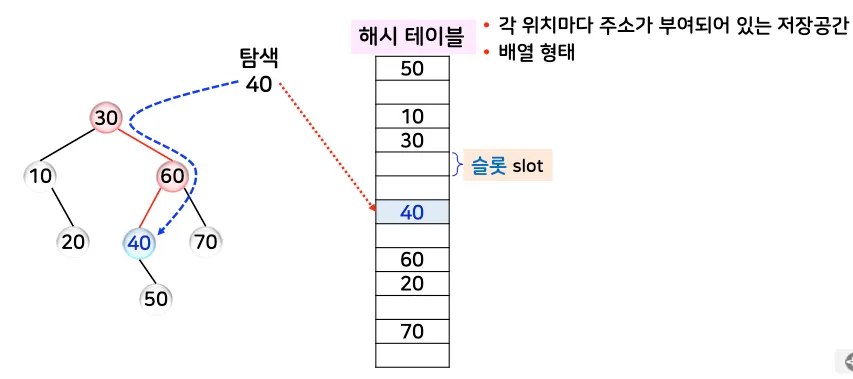
해시 함수: 키값을 테이블의 주소로 변환.
2.
슬롯: 해시 테이블에서 데이터를 저장하는 각 위치
•
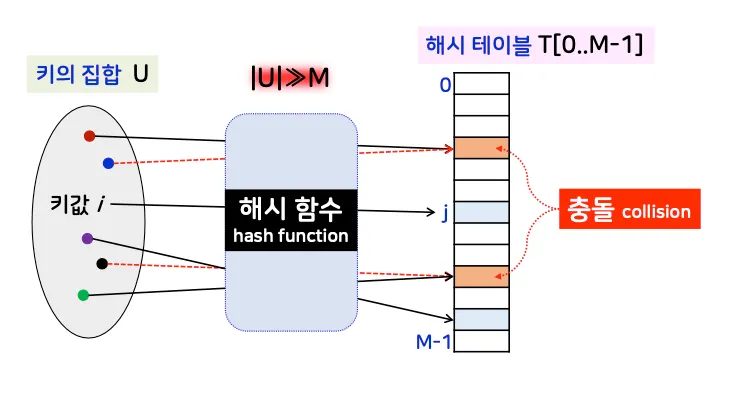
구조
•
해시 함수
◦
정의
▪
키 값을 해시 테이블의 주소로 변환하는 함수
▪
h: U → {0, 1, 2, … M-1 }
◦
종류
▪
제산 잔여법, 비닝, 중간 제곱법, 문자열을 위한 함수 등
◦
바람직한 해시 함수
▪
계산에 용이해야함
▪
적은 충돌 발생 → 균등 분포
3.2. 해시 함수 종류
•
제산 잔여법: 키값을 테이블 크기로 나눈 나머지를 주소로 사용
◦
h(K) = K mod M
▪
K: 키 값, M: 해시 테이블의 크기
▪
M은 소수로 선택하는 것이 바람직
•
비닝: 키값 범위를 나눠 슬롯에 매핑
◦
키 값의 범위를 M 등분하여 각 등분을 각 슬롯으로 해시
◦
상위 비트의 분포가 고르지 못하면 쏠림 현상 발생 가능
•
중간 제곱법: 키값을 제곱 후 비트를 취해 주소 생성
•
문자열 해시
◦
단순 합: 각 문자의 코드값 합 한 후 제산 잔여법 적용
◦
가중 합: 자릿수 가중치 적용 후 제산 잔여법 적용
3.3. 충돌
•
충돌
◦
서로 다른 키 값 x, y에 대하여 h(x) = h(y)인 경우
◦
충돌 해결 방법
▪
개방 해싱
▪
폐쇄 해싱
3.4. 충돌 처리 방법 (1) 개방 해싱
3.4.1. 개념
•
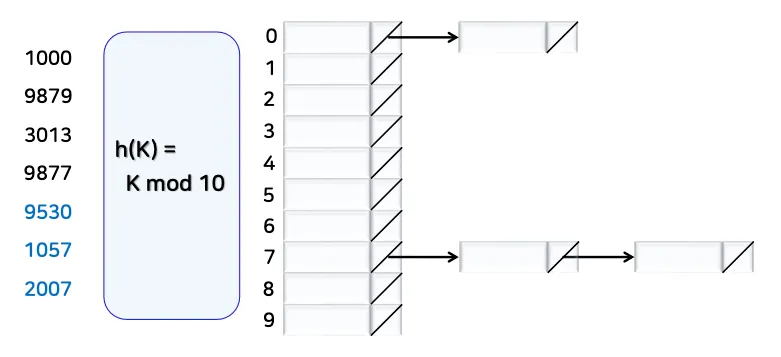
충돌이 발생하면, 해시 테이블 슬롯마다 연결 리스트(Linked List)를 두어 추가로 저장
•
즉, 해시 테이블의 각 슬롯을 연결 리스트의 ‘헤더(head)’처럼 사용하여, 동일한 해시 값을 갖는 모든 키를 연결 리스트로 묶어 보관
•
예시
3.4.2. 특징
•
장점
◦
구현이 직관적이고 간단
◦
해시 테이블 자체가 꽉 차더라도(로드 팩터가 커지더라도) 연결 리스트로 계속 연결할 수 있으므로, 충돌 처리가 비교적 유연
◦
슬롯이 가득 차서 더 이상 자리를 못 찾는 상황이 발생하지 않음
•
단점
◦
연결 리스트가 길어지면, 탐색 시간이 (거의) 연결 리스트 순회 시간이 되므로 평균 탐색 시간이 늘어남
◦
만약 해시 함수를 잘못 설정하여 특정 슬롯에 많은 키가 몰리면 편향(clustering) 문제가 심해짐
◦
링크드 리스트가 메모리를 추가로 사용한다는 점도 고려해야 함
•
기타 특징
◦
보통 주기억장치(메인 메모리) 내에서 해시 테이블을 운영할 때 많이 사용
◦
디스크에서 불러와야 하는 상황(외부 기억장치)에서는, 연결 리스트를 여러 번 접근해야 하므로 디스크 I/O가 증가하여 비효율적이 될 수 있음
3.5. 충돌 처리 방법 (2) 폐쇄 해싱
•
기본 개념
◦
슬롯 자체에 모든 키를 저장하려고 하되, 충돌이 발생하면 테이블 내 다른 슬롯을 찾아가며 저장하는 방식
◦
따라서 테이블 안에 빈 슬롯(empty slot)이 없으면 더 이상 삽입할 수 없음 (오버플로)
•
주요 기법
◦
버킷 해싱(Bucket Hashing)
◦
개방 주소법(Open Addressing)
▪
선형 탐사(Linear Probing)
▪
이차 탐사(Quadratic Probing)
▪
이중 해싱(Double Hashing)
3.6. 폐쇄 해싱 (1) - 버킷 해싱
•
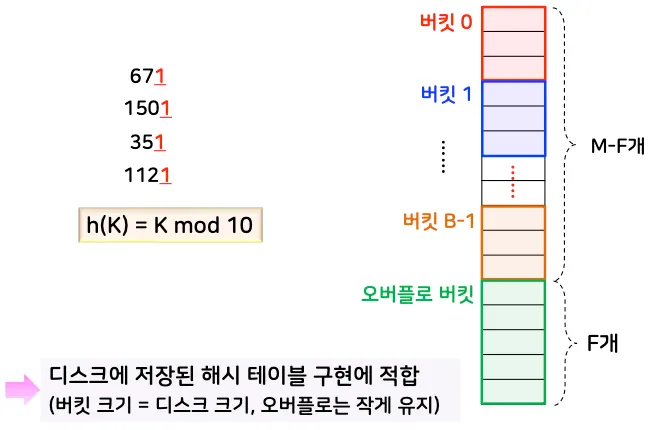
해시 테이블의 슬롯을 하나 이상의 슬롯이 모인 ‘버킷(Bucket)’ 단위로 묶어서 관리하는 기법
◦
예: 해시 테이블의 한 슬롯이 아니라, 한 버킷(Bucket)에 여러 개의 키를 저장할 수 있게 설계
•
디스크를 사용하는 경우에 유리한 방법
◦
버킷 크기를 디스크 블록(페이지) 크기에 맞춤으로써, 한 번 디스크에서 읽어올 때 여러 키를 한꺼번에 가져오는 효과를 얻음
•
오버플로 버킷을 두어, 기본 버킷이 꽉 찼을 때는 오버플로 버킷에 데이터를 저장
◦
연결 리스트처럼, 오버플로 버킷을 계속 연결할 수도 있음
◦
다만, 너무 길어지면 성능 저하가 발생
3.7. 폐쇄 해싱 (2) - 개방 주소법
•
기본 아이디어
◦
충돌이 발생하면, 해시 테이블 내에서 다른 ‘비어 있는 슬롯’을 순차적으로 찾아 키를 삽입하는 기법
◦
즉, 슬롯 한 개당 하나의 키만 저장하고, 슬롯이 이미 차있다면 새로운 슬롯을 탐색(probe)하여 빈 자리를 확보
•
탐사 함수(Probe sequence)의 개념
◦
어떤 키 K를 삽입(또는 검색)하려 할 때, 첫 홈(home) 위치 h(K)가 이미 차있다면, 다음과 같은 식으로 탐사 순서를 결정
◦
M: 해시 테이블의 크기(슬롯 개수)
◦
Δ(i): 충돌 시마다 다음으로 이동할 슬롯의 오프셋(offset)을 결정하는 함수
◦
i=0,1,2,…,M−1
•
Δ(i)를 어떻게 정의하느냐에 따라, 다음 기법으로 세분화
1.
선형 탐사(Linear Probing)
2.
이차 탐사(Quadratic Probing)
3.
이중 해싱(Double Hashing)
3.7.1. 선형 탐사
•
탐사 순서
◦
홈 위치가 사용 중이면 빈 슬롯을 찾을 때까지 테이블의 다음 슬롯으로 순차적으로 이동
◦
가장 간단하지만 최악의 방법
•
예시
•
단점: 1차 클러스터링 문제
◦
특정 영역(slots)에 데이터가 많이 몰려서 클러스터(cluster)가 생기면, 새 데이터 역시 그 클러스터 바로 옆에 붙게 됨
◦
이로 인해 클러스터가 더 커지고, 탐사 횟수도 증가하여 성능 저하가 발생
◦
그리고 모든 키가 같은 탐사 경로를 따라가므로, 한 번 몰리기 시작하면 악화되기 쉬움
3.7.2. 이차 탐사
•
탐사 순서의 계산에 이차식을 이용
◦
충돌이 발생하는 횟수의 제곱 형태로 탐사 순서를 결정
•
서로 다른 홈 위치를 갖는 두 키는 서로 다른 탐사 순서를 가짐
◦
p(K, i) = (h(K) + i^2) mod 10
▪
h(K1) = 1 → 1, 2, 5, 0, …
▪
h(K2) = 4 → 4, 5, 8, 3, …
위 예시 부연설명
•
예시
•
특징
◦
모든 슬롯이 탐사 순서에 사용되지 않음
▪
p(K, i) = (h(K) + i^2) mod 10
•
p(K, 0)=1 → 슬롯 0, 1, 2, 5, 6, 7만 탐사 가능→ 슬롯 3, 4, 8, 9는 사용 불가
▪
탐사 함수와 해시 테이블 크기가 적절히 조합되면 많은 슬롯의 방문이 가능
◦
2차 클러스터링 문제
▪
동일한 홈 위치를 갖는 두 키는 동일한 탐사 순서를 가짐
•
특정한 홈 위치에 대한 클러스터를 만드는 현상
3.7.3. 이중 해싱
•
탐사 순서를 원래의 키값을 이용하여 해싱
◦
1차/2차 클러스터링 문제 해결
◦
서로 다른 두 키의 홈 위치가 동일해도 서로 다른 탐사 순서를 가짐
•
조건
◦
h2(K)가 0이 되면 안 됨
◦
보통 M을 소수(prime)로 설정하고,
▪
h2(K) 가 1 이상 M−1이하의 값이 되도록 하는 방식(서로소가 되도록)
▪
혹은 M=2^m으로 잡고, h2(K)가 홀수만 반환하도록 하는 방식을 씀
◦
이러한 조건을 만족해야 모든 슬롯을 방문(탐사)할 수 있으므로, 탐색 효율이 좋아짐
3.8. 데이터 삭제
•
두 가지 고려 사항
◦
데이터의 삭제가 차후의 탐색을 방해하지 말아야 함
◦
단순히 빈 슬롯으로 두면 탐색이 해당 슬롯에서 종료되므로 그 이후의 데이터는 고립됨
◦
삭제로 생긴 빈 슬롯은 나중에 삽입 과정에서 사용되어야 함
•
비석 tombstone
◦
삭제된 데이터의 위치에 ’비석’이라는 특별한 표시를 하는 방법
▪
탐색 → 탐색하는 동안 비석을 만나면 탐색을 계속 진행
▪
삽입 → 비석이 표시된 위치를 빈 위치로 간주하여 새 데이터를 삽입
◦
비석의 개수가 증가할수록 평균 탐색 거리가 증가