Total
Search
1. 기본 개념
1.1. 그래프의 정의
•
그래프 G → G = (V, E)
◦
V: 정점(Vertex)의 집합
◦
E: 간선(Edge)의 집합
•
그래프의 종류
1.
무방향 그래프 (Undirected Graph): 간선의 방향이 없음
2.
방향 그래프 (Directed Graph): 간선의 방향이 있음
3.
가중 그래프 (Weighted Graph): 간선에 가중치가 부여됨
1.2. 주요 용어
•
인접(Adjacent): 두 정점이 간선으로 연결되어 있을 때
•
부수(Incident): 정점과 간선이 연결되어 있을 때
•
부분 그래프(Subgraph): 주어진 그래프의 부분 집합으로 구성된 그래프
•
경로(Path): 정점과 간선의 연속적인 열
•
경로의 길이: 경로에 포함된 간선의 수
•
차수(Degree)
◦
진입 차수(In-degree): 방향 그래프에서 정점으로 들어오는 간선의 수
◦
진출 차수(Out-degree): 방향 그래프에서 정점에서 나가는 간선의 수
•
단순 경로(Simple Path): 중복 간선 없이 정점을 방문하는 경로
•
사이클(Cycle): 시작 정점과 종료 정점이 동일한 경로
•
루프(Loop): 하나의 정점에서 시작하여 다시 자기 자신으로 돌아오는 간선
•
연결성(Connectedness)
◦
강하게 연결(Strongly Connected): 방향 그래프에서 모든 정점 간 양방향 경로 존재
◦
약하게 연결(Weakly Connected): 방향 무시 시 연결된 상태
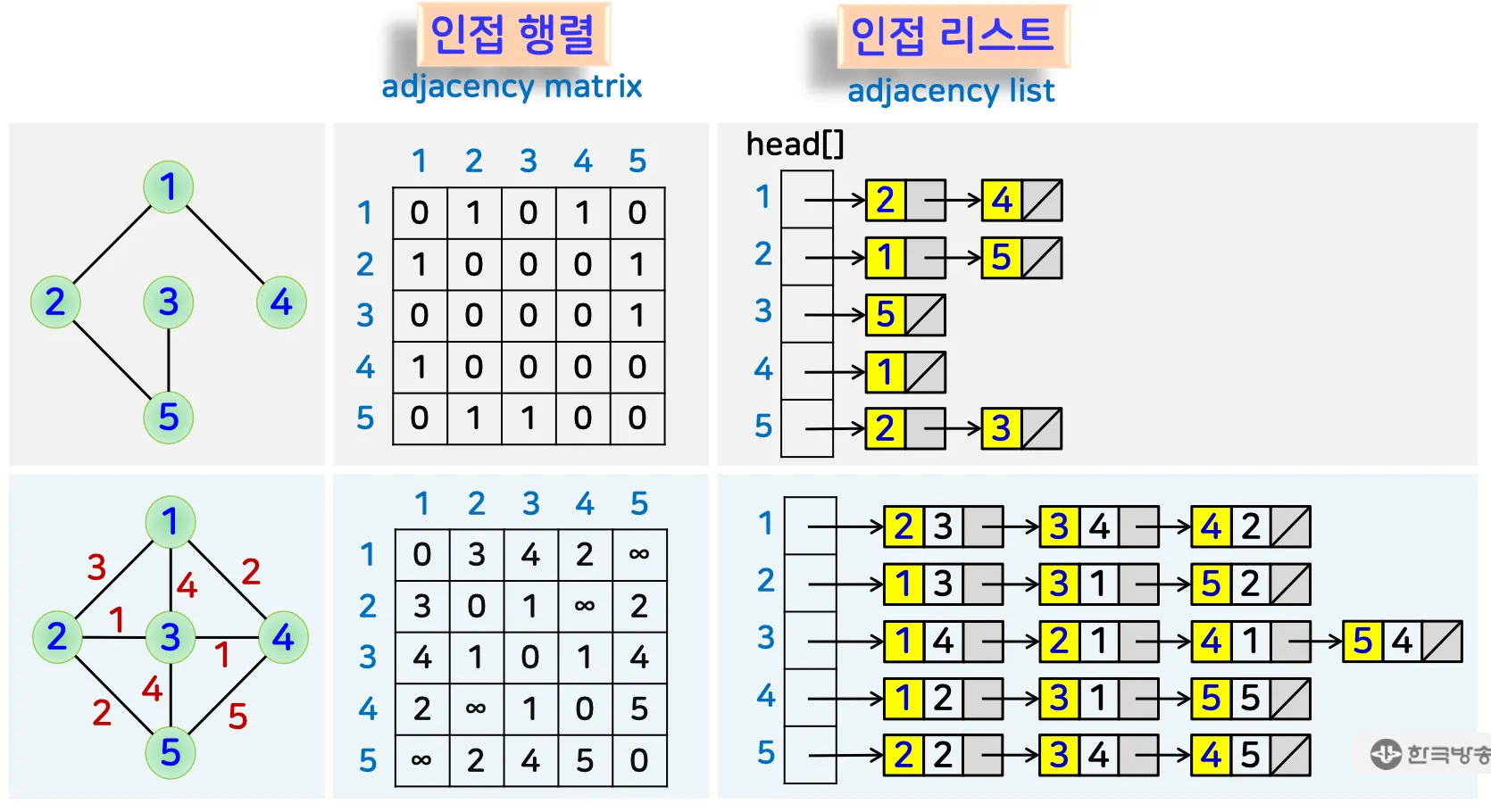
1.3. 그래프의 구현
•
인접 행렬 (Adjacency Matrix)
◦
정점 수 의 제곱 크기 행렬로 표현 |V| * |V|
◦
조밀 그래프 (Dense Graph)에 적합
•
인접 리스트 (Adjacency List)
◦
각 정점마다 연결 리스트로 이웃한 정점을 기록.
◦
성긴 그래프 (Sparse Graph)에 적합
2. 그래프 순회
•
그래프의 모든 정점을 체계적으로 한 번씩 방문하는 방법
2.1. 깊이 우선 탐색 (DFS)
•
동작 방식
◦
정점 하나를 선택 후 가능한 한 깊게 탐색
◦
더 이상 갈 곳이 없으면 뒤로 돌아가 탐색하지 않은 경로를 계속 진행
•
시간 복잡도
◦
인접 리스트 O(|V| + |E|)
◦
인접 행렬 O(|V|^2)
•
스택을 활용한 구현
DepthFirstSearch (G, s) { // G: 입력 그래프, s: 시작 정점
Push(Stack, s);
while (Stack != NULL) {
c = Stack의 top에 있는 정점;
c.visited = TRUE;
정점 c를 방문 정점으로 출력;
do {
for (v ← c의 모든 인접한 정점) {
if (v.visited == FALSE)
Push(Stack, v) 후 while문으로 이동;
}
c = Pop(Stack);
} while (Stack != NULL);
}
}
C
복사
def DepthFirstSearch(G, s): # G: 입력 그래프, s: 시작 정점
Stack = []
Stack.append(s) # 시작 정점을 스택에 삽입
while Stack: # 스택이 비어 있지 않은 동안 반복
c = Stack[-1] # 스택의 top에 있는 정점을 가져옴
c.visited = True # 정점 c를 방문으로 표시
print(f"정점 {c} 방문") # 정점 c를 방문 정점으로 출력
has_unvisited = False # 방문하지 않은 정점 여부를 확인
for v in G.adjacent(c): # c의 모든 인접한 정점을 확인
if not v.visited:
Stack.append(v) # 방문하지 않은 정점을 스택에 삽입
has_unvisited = True
break # 새로운 정점을 방문했으므로 반복 종료
if not has_unvisited:
Stack.pop() # 방문할 정점이 없으면 스택에서 제거
Python
복사
•
재귀를 활용한 구현
DFS_recursion (G, current) {
current.visited = TRUE;
방문 정점으로 current 출력;
for (next ← current의 모든 인접한 정점) {
if (next.visited == FALSE)
DFS_recursion(G, next);
}
}
C
복사
def DFS_recursion(G, current):
current.visited = True # 현재 정점을 방문으로 표시
print(f"방문 정점: {current}") # 방문 정점을 출력
for next_node in G.adjacent(current): # current의 모든 인접한 정점 확인
if not next_node.visited: # 방문하지 않은 정점이 있을 경우
DFS_recursion(G, next_node) # 재귀 호출
Python
복사
2.2. 너비 우선 탐색 (BFS)
•
동작 방식
◦
시작 정점에서 가까운 정점부터 탐색
◦
큐를 사용하여 주변 정점을 순차적으로 관리
•
시간 복잡도
◦
인접 리스트 O(|V| + |E|)
◦
인접 행렬 O(|V|^2)
•
구현
BFS (G, s) {
Enqueue(Queue, s);
s.flag = TRUE;
while (Queue != NULL) {
c = Dequeue(Queue);
정점 c를 방문 정점으로 출력;
for (v ← c의 모든 인접한 정점) {
if (v.flag == FALSE) {
Enqueue(Queue, v);
v.flag = TRUE;
}
}
}
}
C
복사
from collections import deque
def BFS(G, s):
Queue = deque() # 큐 생성
Queue.append(s) # 시작 정점을 큐에 삽입
s.flag = True # 시작 정점을 방문 표시
while Queue: # 큐가 비어있지 않을 동안 반복
c = Queue.popleft() # 큐에서 정점을 꺼냄
print(f"방문 정점: {c}") # 정점 c를 방문 정점으로 출력
for v in G.adjacent(c): # c의 모든 인접한 정점을 확인
if not v.flag: # 방문하지 않은 정점일 경우
Queue.append(v) # 큐에 삽입
v.flag = True # 방문 표시
Python
복사
3. 그래프 순회의 응용
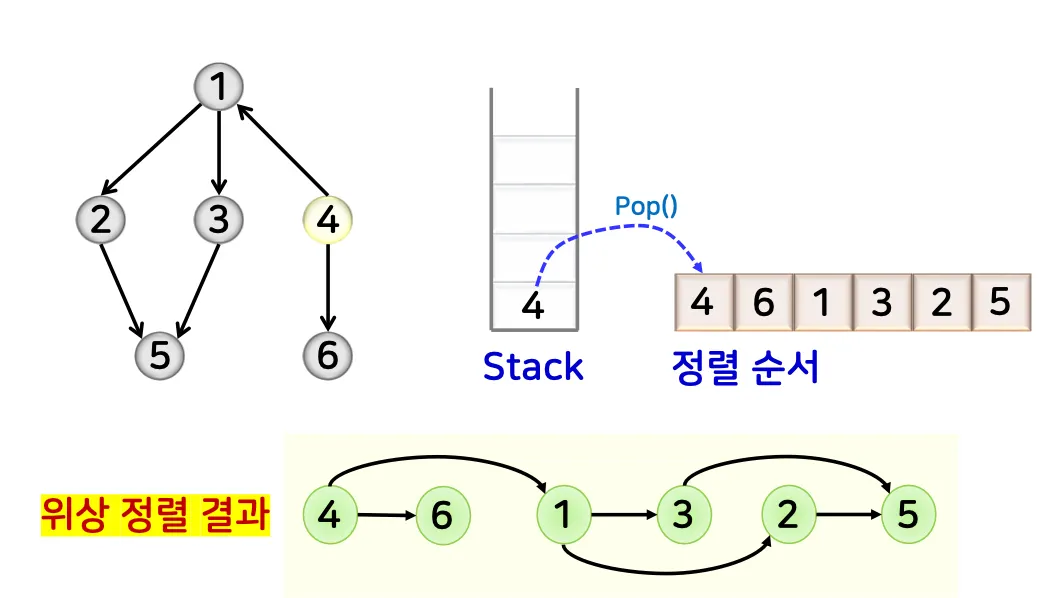
3.1. 위상 정렬
•
정의
◦
방향 비순환 그래프(DAG)에서 모든 정점을 간선의 방향에 맞춰 한 줄로 정렬
◦
무사이클 방향 그래프에서 모든 간선이 한 방향으로만 향하도록 정점을 한줄로 나열하는 것
•
알고리즘
1.
DFS를 수행하며 스택에 정점을 저장
2.
스택에서 꺼낸 순서의 역순으로 정렬
•
예시
•
활용
◦
작업 스케줄링, 의존성 그래프
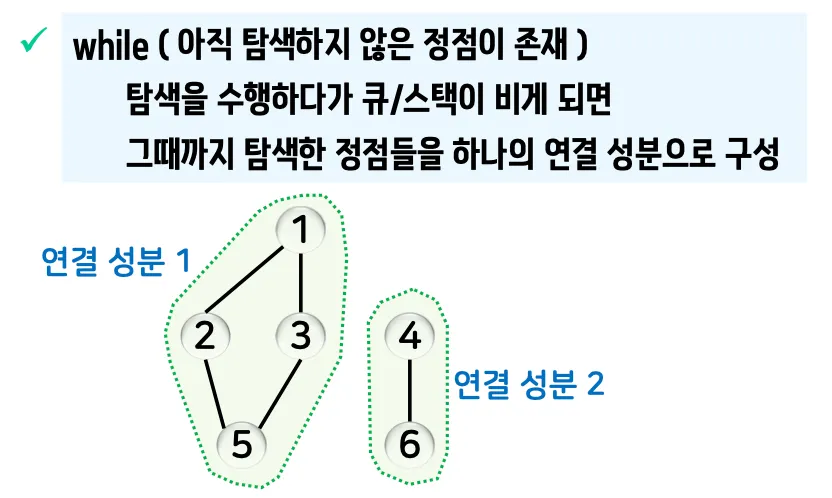
3.2. 그래프의 연결성
•
정의
◦
정점 간의 연결 관계를 다루는 것
•
연결 성분
◦
정의
▪
무방향 그래프에서 연결된 최대 정점 집합
▪
무방향 그래프에서 임의의 두 정점 간의 경로가 존재하는 최대 부분 그래프
◦
알고리즘
▪
DFS 또는 BFS를 수행하며, 연결된 모든 정점을 하나의 성분으로 그룹화
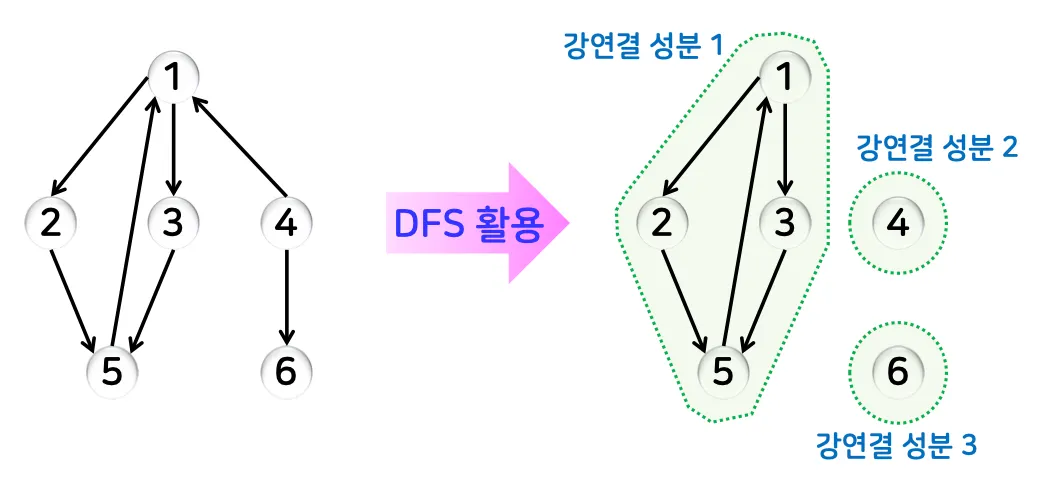
•
강연결 성분
◦
정의
▪
방향 그래프에서 양방향 경로가 존재하는 최대 정점 집합
▪
방향 그래프에서 임의의 두 정점 사이에 양방향의 경로가 존재하는 최대 부분 그래프
◦
알고리즘
1.
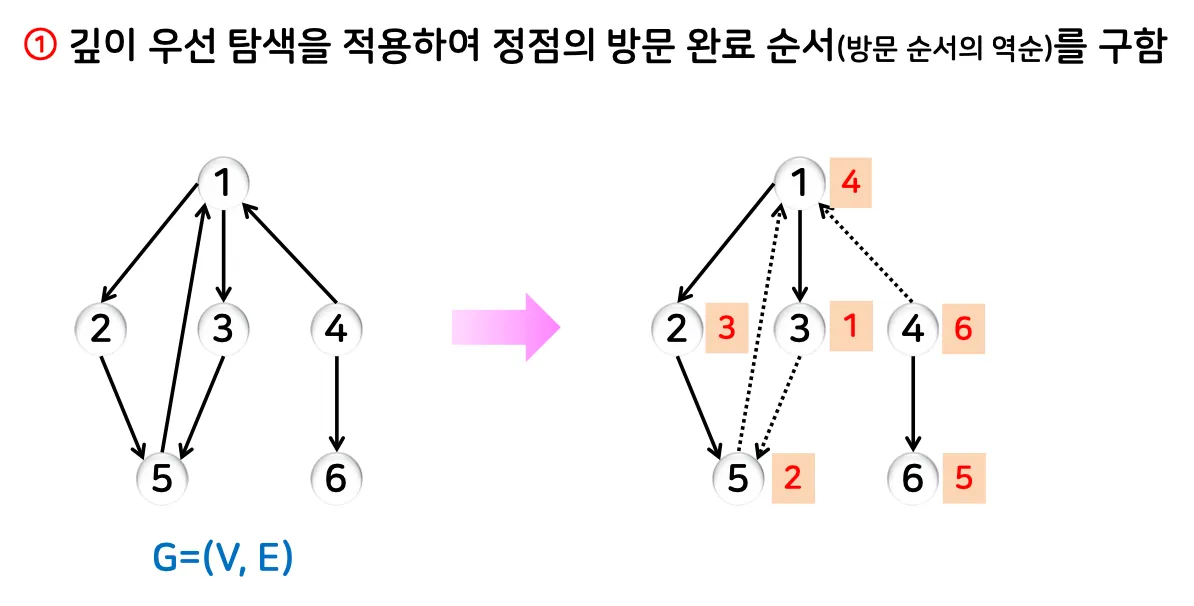
DFS를 수행하여 각 정점의 방문 완료 순서(방문 순서의 역순) 기록
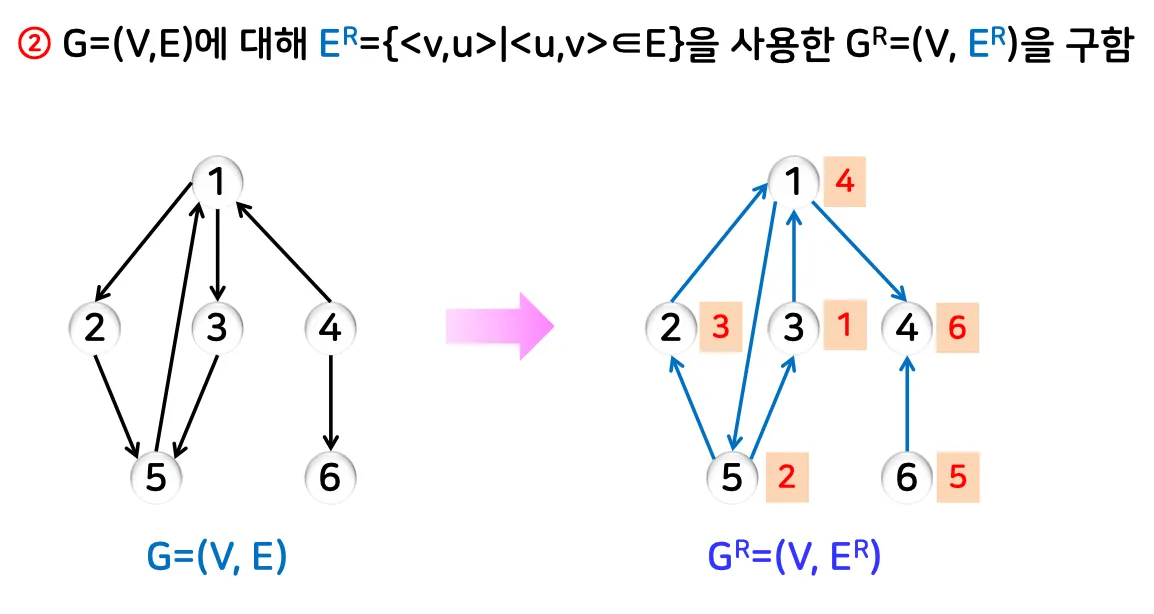
2.
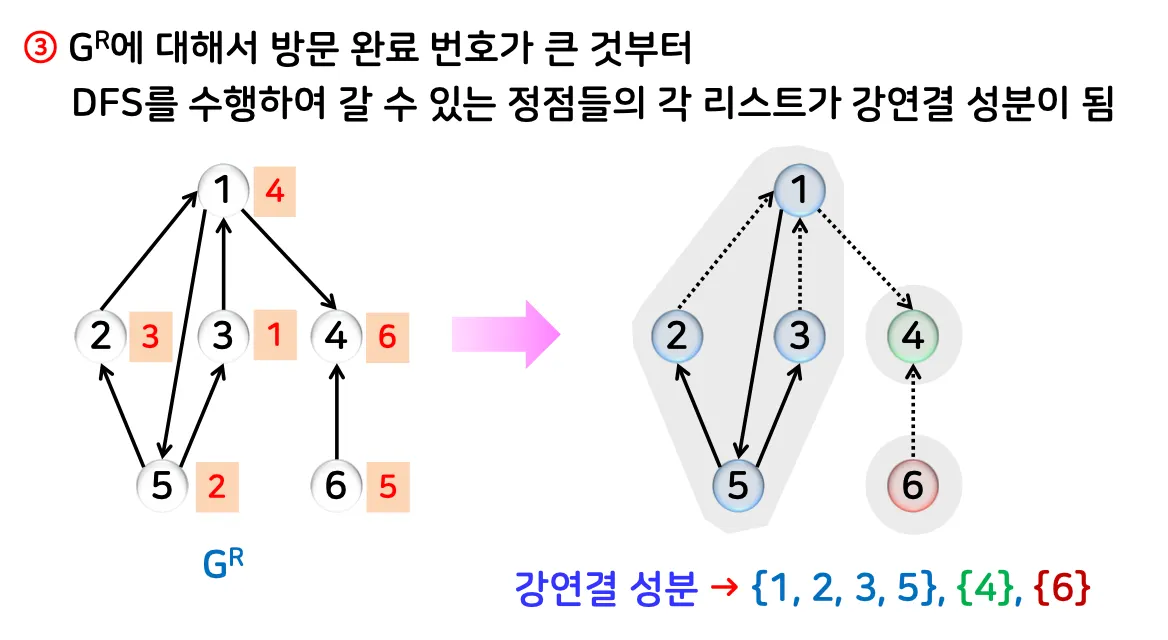
간선의 방향을 뒤집은 그래프에서, 방문 완료 순서의 역순으로 DFS 수행.
3.
각 DFS 결과를 강연결 성분으로 처리.
◦
예시