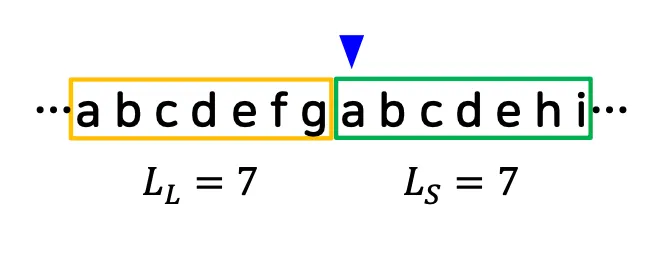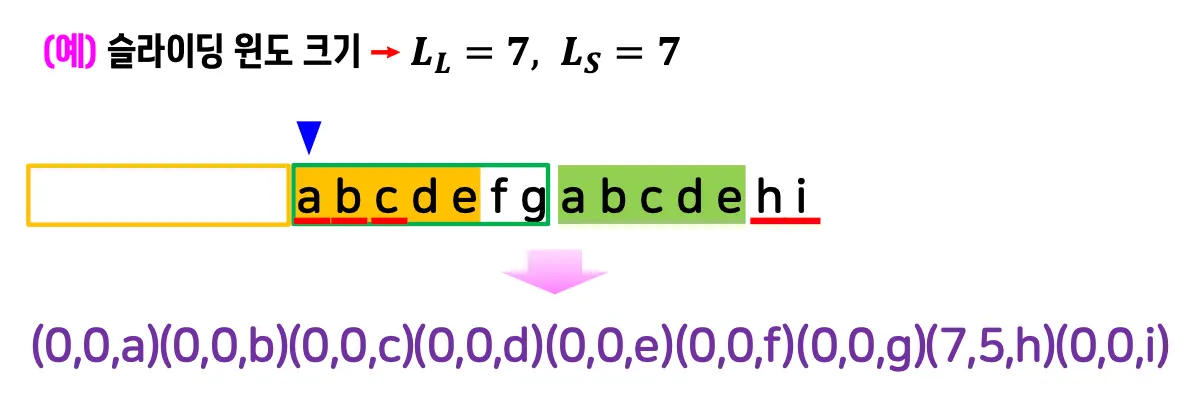Total
Search
1. 데이터 압축 기본 개념
1.1. 개념
•
주어진 데이터를 보다 적은 공간을 사용하여 표현하는 것
•
데이터 → 1차원(스트링), 2차원(이미지), 3차원(동영상) 등
1.2. 데이터 압축 구분
•
무손실 압축
◦
압축된 데이터로부터 원래의 데이터를 완벽하게 복원할 수 있는 압축 방법
◦
데이터의 내용 하나하나가 모두 중요한 경우에 사용
◦
종류 → RLE, 허프만 코딩, LZ77 등
•
손실 압축
◦
압축된 데이터로부터 원래의 데이터를 완벽하게 복원할 수 없는 압축 방법
◦
데이터의 내용이 약간 변형되어도 무방한 경우에 사용
◦
종류 → JPEG 표준, MPEG 표준 등
1.3. 데이터 압축 기본 용어
•
인코딩 encoding
◦
원래의 데이터를 압축된 데이터로 변환하는 것
•
디코딩 decoding
◦
압축된 데이터를 압축되지 않은 데이터로 변환하는 것
◦
손실 압축의 경우 디코딩 결과가 인코딩 이전 데이터와 동일하지 않을 수 있음
2. RLE (Run Length Encoding)
2.1. 개념
•
스트링에서 동일 문자가 연속해서 나타나는 것(Run)을 그 문자와 반복 횟수로 압축하는 방법
•
예)
◦
bbbbb → (b,5)
2.2. 인코딩
•
주어진 스트링을 차례대로 보며 문자가 달라질 때까지 횟수를 샘
•
예) aaabbbbbaaccccbaaaaaaa
→ (a,3)(b,5)(a,2)(c,4)(b,1)(a,7)
RLE_enc(n, S[])
{
int idx = 0;
for (i = 0; i < n; i++) {
count = 1;
while (i + 1 < n && S[i] == S[i + 1]) {
count++;
i++;
}
C[idx++] = (S[i], count);
}
return (C[0..idx - 1]);
}
C
복사
2.3. 디코딩
•
압축된 데이터를 차례로 보며 각 문자를 횟수만큼 반복
•
예) (a,3)(b,5)(a,2)(c,4)(b,1)(a,7)
→ aaabbbbbaaccccbaaaaaaa
RLE_dec(m, C[])
{
int i = 0;
for (idx = 0; idx < m; idx++)
for (j = 0; j < C[idx].count; j++, i++)
S[i] = C[idx].ch;
return (S[0..i - 1]);
}
C
복사
2.4. 성능
•
성능 → O(n)
◦
인코딩과 디코딩 모두 이중 루프로 보이지만
◦
실제로는 스트링의 길이(n)만큼 수행
3. 허프만 코딩 (Huffman coding)
3.1. 개념
•
스트링에서 각 문자의 빈도 정보를 이용하는 통계적 압축 방법
◦
빈도수가 큰 문자 → 짧은 코드
◦
빈도수가 작은 문자 → 긴 코드
•
예시)
◦
a b a b a b c d b a b c
▪
a, b → 빈도수가 큰 문자
▪
c, d → 빈도수가 작은 문자
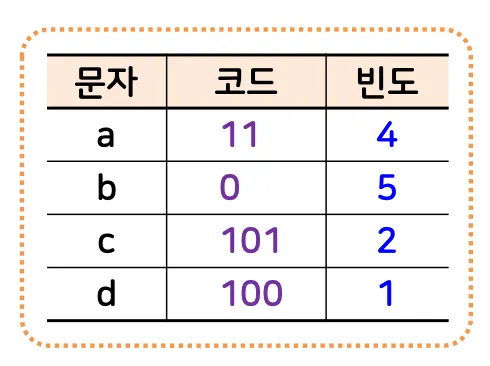
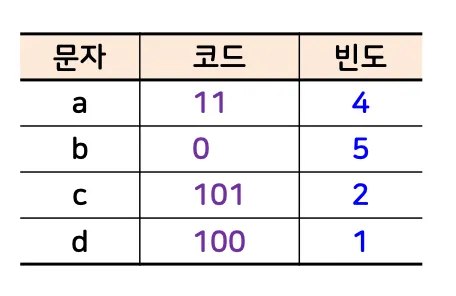
→ 1101101101011000110101
3.2. 허프만 트리
•
각 문자에 이진 코드를 부여하기 위한 전(full) 이진 트리
◦
모든 노드는 자식 노드의 개수가 2개 또는 0개(리프 노드)
◦
각 리프 노드는 각 문자를 표시
•
허프만 트리의 생성 방법: 욕심쟁이 방법, 상향식
◦
욕심쟁이: 선택 중 가장 최선
◦
상향식: 리프노드 → 루트 노드순으로 생성
•
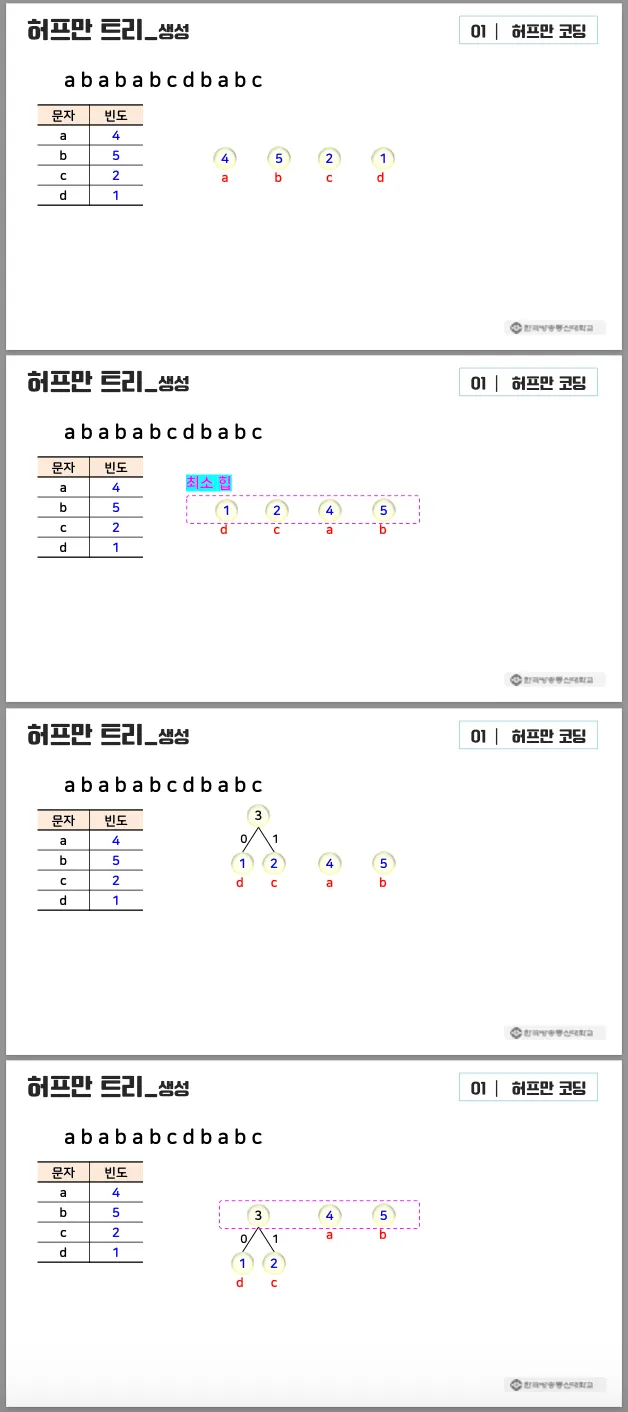
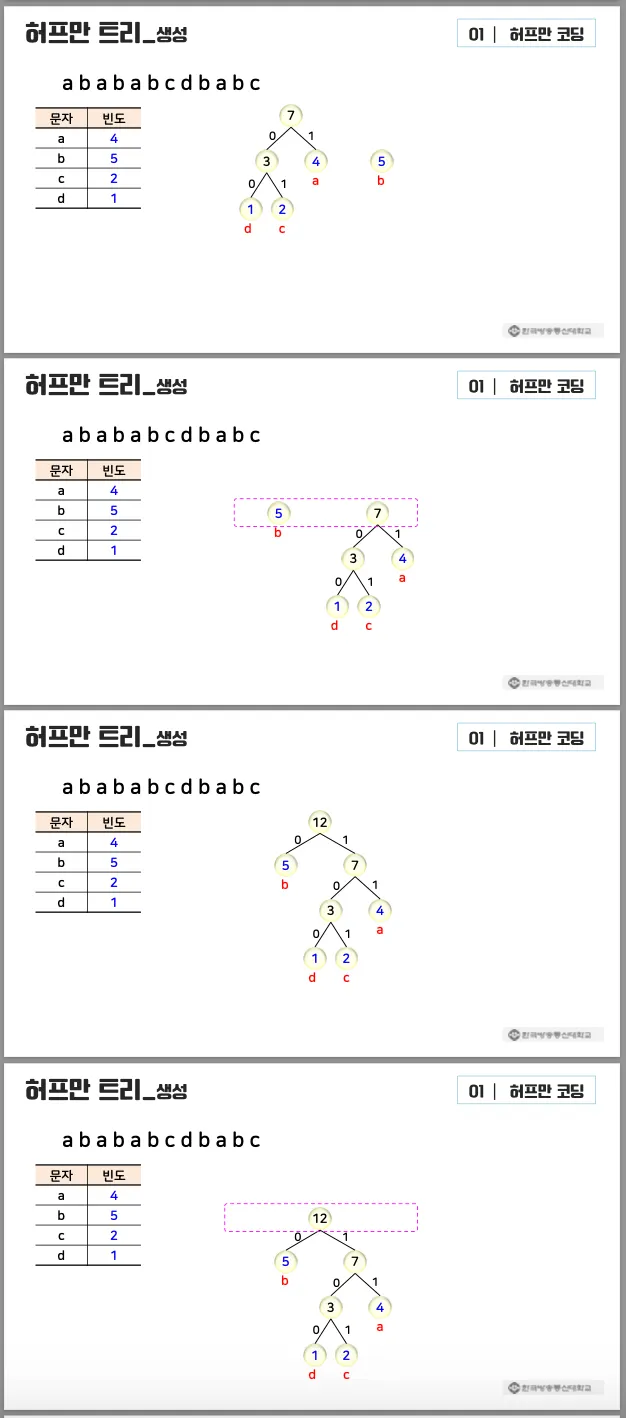
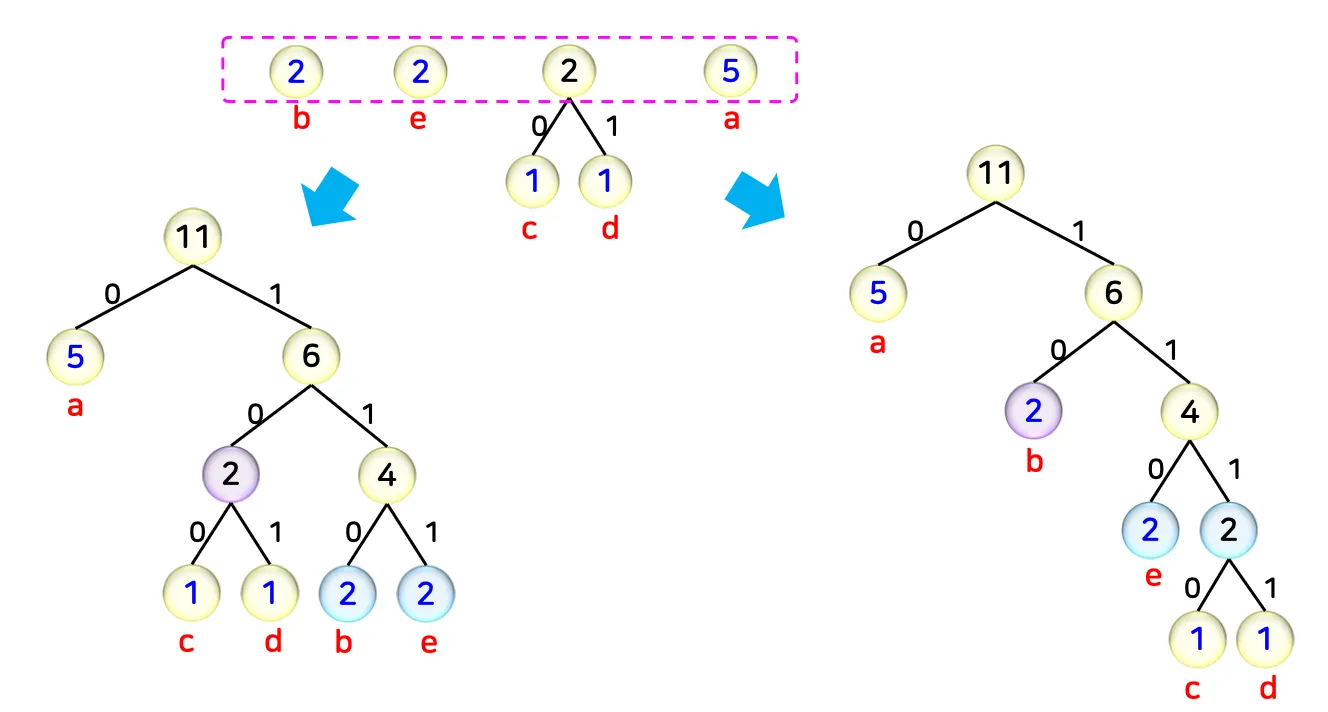
과정
1.
각 문자 → 노드 하나인 트리
a.
노드의 레이블 → 문자의 빈도수
2.
루트 노드의 레이블이 가장 적은 두 트리 선택 → 한 트리로 합침
(빈도수가 가장 적은 문자2를 선택한다는 것을 의미)
a.
두 루트 노드를 자식 노드로 갖는 새로운 노드 생성
b.
새로운 노드의 레이블 → 자식 노드의 레이블의 합
c.
두 간선의 레이블 → 각각 0과 1
3.
남은 트리가 둘 이상 → 2로 이동
•
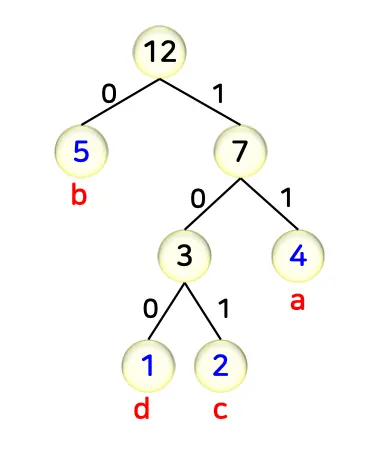
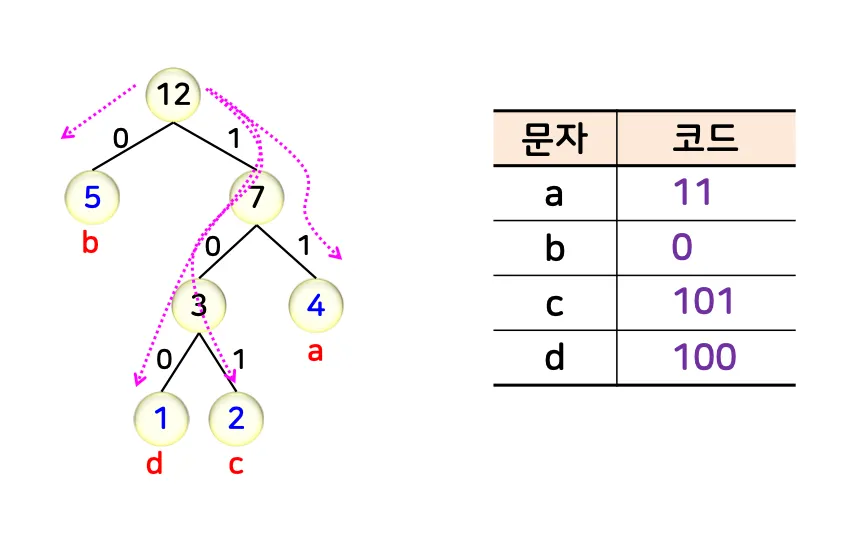
예시
•
루트 노드로부터 리프 노드까지의 간선의 레이블 생성
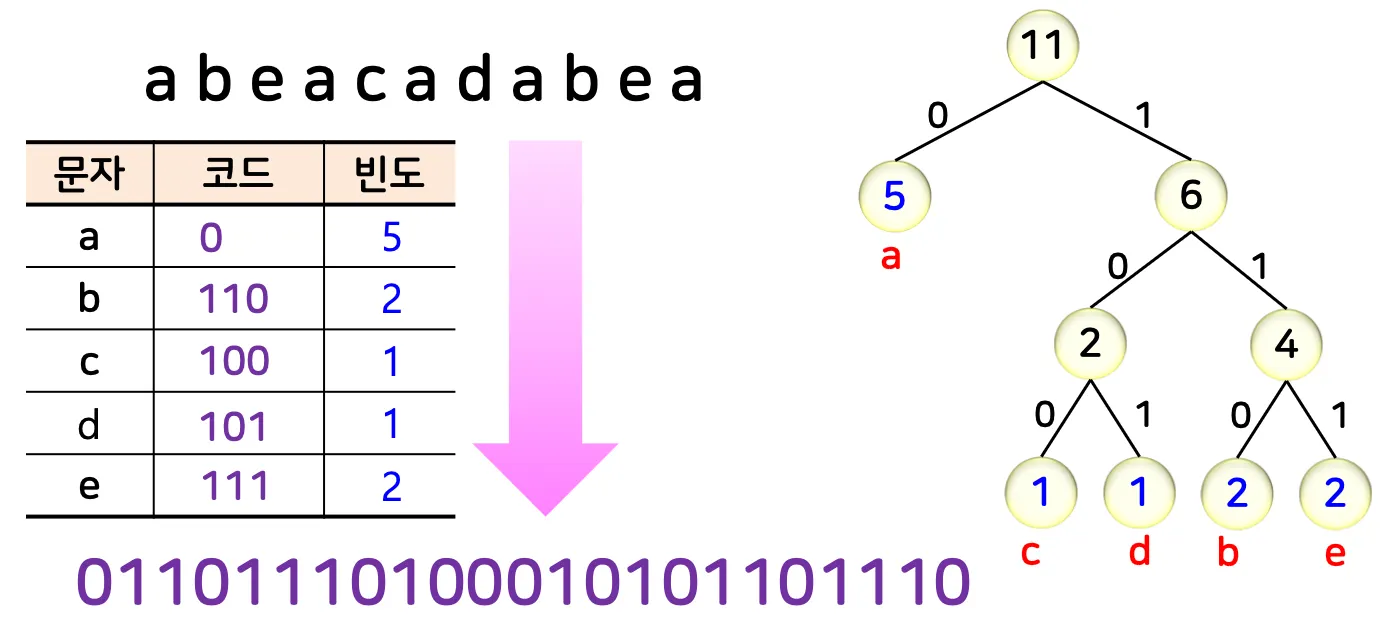
3.3. 인코딩
1.
주어진 스트링에서 각 문자의 출현 빈도수 계산
2.
각 문자의 빈도수를 이용하여 허프만 트리를 만들어 각 문자에 이진 코드 부여
3.
주어진 스트링의 각 문자를 이진 코드로 변환하여 압축된 스트링 생성
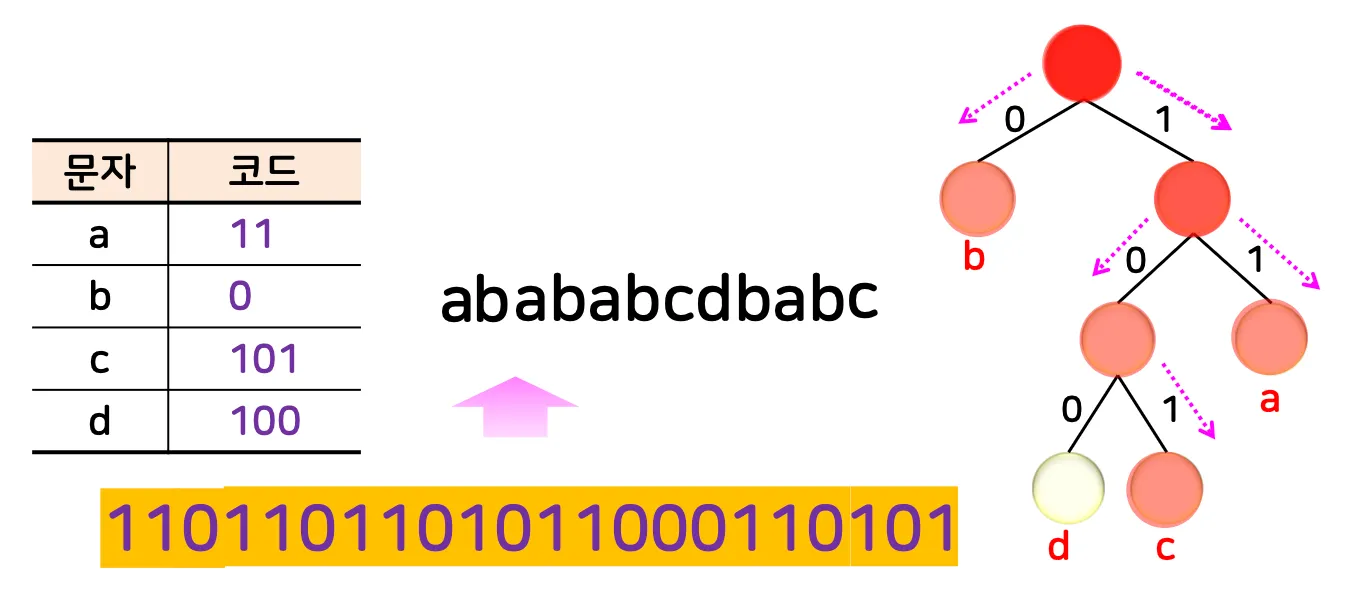
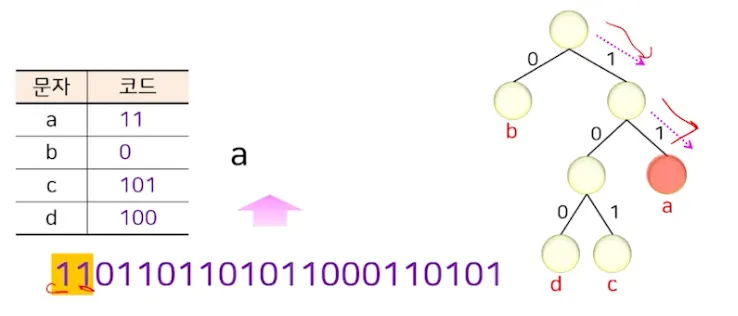
3.4. 디코딩
1.
허프만 트리의 루트 노드에 위치
2.
압축된 스트링을 1비트씩 읽으며 자식 노드로 내려감
3.
리프 노드에 도착하면 그 노드에 해당하는 문자 출력 후 ①로 이동
•
부분 예시
◦
리프노드를 만날때까지 내려감
◦
11 → a
3.5. 성능과 특징
•
인코딩 성능 → O(|∑|log|∑|+n)
◦
각 문자의 빈도수 계산 → O(n)
◦
허프만 트리 생성 및 이진 코드 생성 → O(|∑|log|∑|)
▪
최소 힙 구축 → O(|∑|)
▪
알파벳 크기(|∑|)만큼 힙에서 최솟값 삭제와 삽입(O(log|∑|)) 반복하며 트리 생성
▪
트리 순회하며 각 문자의 이진 코드 추출 → O(|∑|)
◦
스트링의 길이 만큼 수행 → O(n)
•
디코딩 성능 → O(|∑|log|∑|+m)
◦
허프만 트리 생성 → O(|∑|log|∑|)
◦
압축된 비트 스트링의 길이 만큼 수행 → O(m)
•
각 문자에 부여하는 코드는 접두부 코드이며 최적의 코드
◦
접두부 코드
▪
각 문자에 부여된 이진 코드가 다른 문자에 부여된 이진 코드의 접두부가 되지 않는 것
◦
최적의 코드
▪
인코딩된 스트링의 길이가 가장 짧음
•
허프만 트리는 유일하지 않을 수 있음
◦
같은 빈도수를 갖는 노드들이 존재하면 허프만 트리 모양이 달라질 수 있음
4. LZ77
4.1.개념
•
스트링에서 한 번 나왔던 문자열이 다시 나오면 앞서 나온 위치와 길이 그리고 바로 다음 문자로 변환하여 압축하는 방법
4.2. 슬라이딩 윈도우
•
스트링에서 일정 크기의 범위만 참조하도록 제한
•
위치 이동 가능
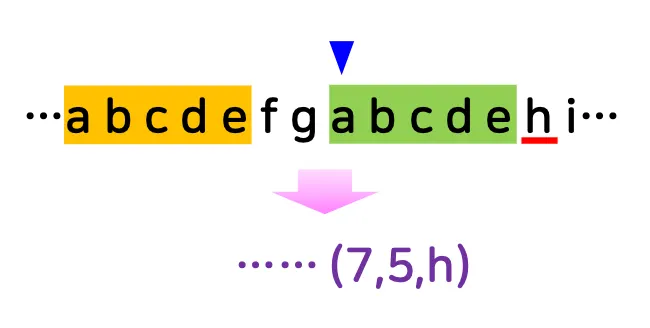
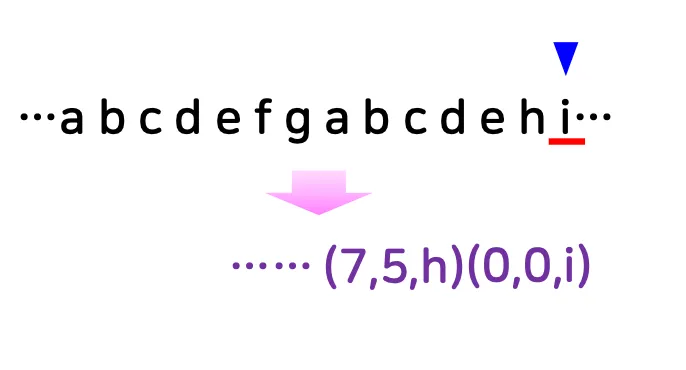
4.3. 인코딩
•
주어진 스트링을 차례로 보며 슬라이딩 윈도 안에서
(매치의 시작 위치 사이의 거리, 매치 길이, 다음 문자)로 변환
4.4. 디코딩
•
압축된 데이터를 차례로 보며 디코딩 중인 스트링에서 거리만큼 앞쪽에서 길이만큼 문자를 출력 후 다음 문자 출력
4.5. 성능 및 특징
•
허프만 코딩 알고리즘과 함께 zip에 사용됨
◦
DEFLATE (RFC 1951) 알고리즘
•
LZ78, LZW 등 다양한 LZ- 계열 알고리즘 존재
5. 영상 압축
•
2차원 이미지나 3차원 동영상이 갖는 특성을 압축에 반영
◦
2차원 이미지 → 인접한 픽셀 정보 유사성
◦
3차원 동영상 → 인접한 시간의 영상들의 유사성
•
2차원 이미지 압축 → JPEG, GIF, TIFF, PNG 등
◦
JPEG 표준은 2차원 데이터를 단위 블록으로 나눈 뒤 블록별로 압축하는 방법
•
3차원 동영상 압축 → MPEG 표준
◦
MPEG 표준은 시간순으로 나열된 2차원 데이터를 연속된 시간의 특성을 이용하여 압축하는 방법