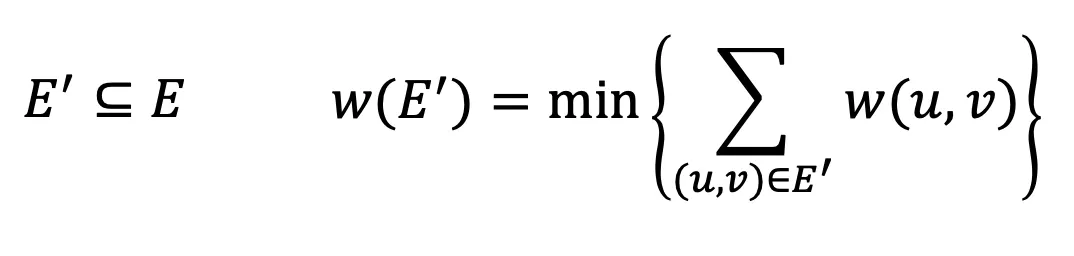Total
Search
1. 최소 신장 트리 (MST)
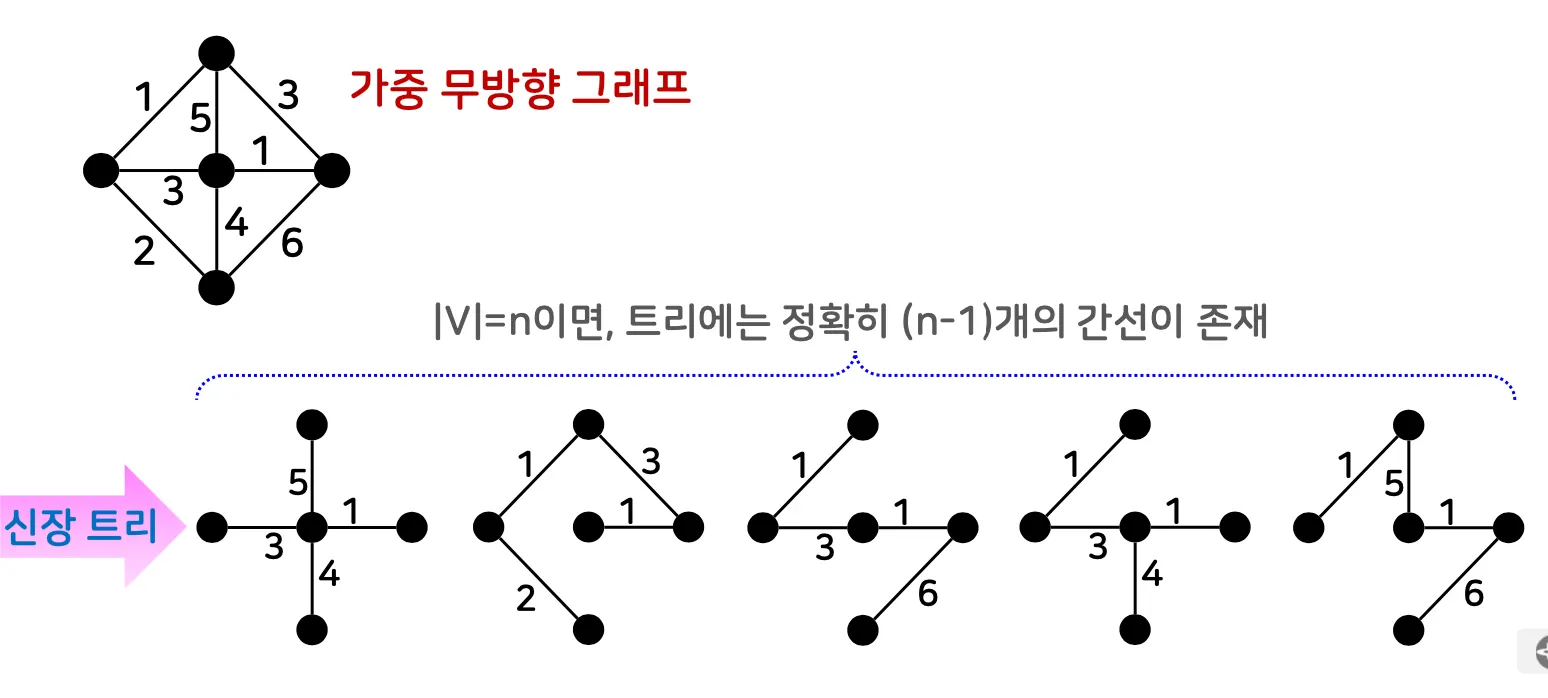
1.1. 신장 트리
•
가중 무방향 그래프에서 모든 정점을 포함하는 트리
1.2. 최소 신장 트리
•
정의
◦
간선 (u, v)마다 가중치 w(u, v)를 가진 연결된 무방향 그래프 G=(V, E)에 대해서 다음을 만족하는 트리 G’=(V, E’)
◦
신장 트리 중에서 가중치의 합이 가장 작은 것
•
최소 신장 트리 알고리즘
◦
모든 간선 중에서 정점을 모두 연결하면서 가중치의 합을 가장 작게 만드는 (n-1)개의 간선을 고르는 과정
Greedy_MST ( G )
{
T ← Ø; // 최소 신장 트리의 간선 집합
while ( T가 신장 트리를 만들지 않았음 ) {
// 최선의 간선: 사이클을 형성하지 않으며 최소한의 가중치를 갖는 간선
최선의 간선 (u, v) 선택;
T ← T ∪ { (u, v) };
}
return (T);
}
C
복사
◦
욕심쟁이 방법 적용
▪
크루스칼, 프림
2. 크루스칼 알고리즘
2.1. 개념
•
정의
◦
최소 신장 트리를 생성하는 알고리즘으로, 가중 무방향 그래프의 간선 중에서 가중치가 가장 작은 간선부터 하나씩 추가.
◦
사이클을 형성하지 않는 선에서 간선을 추가하여, 최소 비용의 신장 트리를 생성
•
사이클 형성 여부의 판단
◦
간선 (u, v)의 두 정점 u, v가 서로 다른 연결 성분에 속하면 사이클이 발생하지 않음
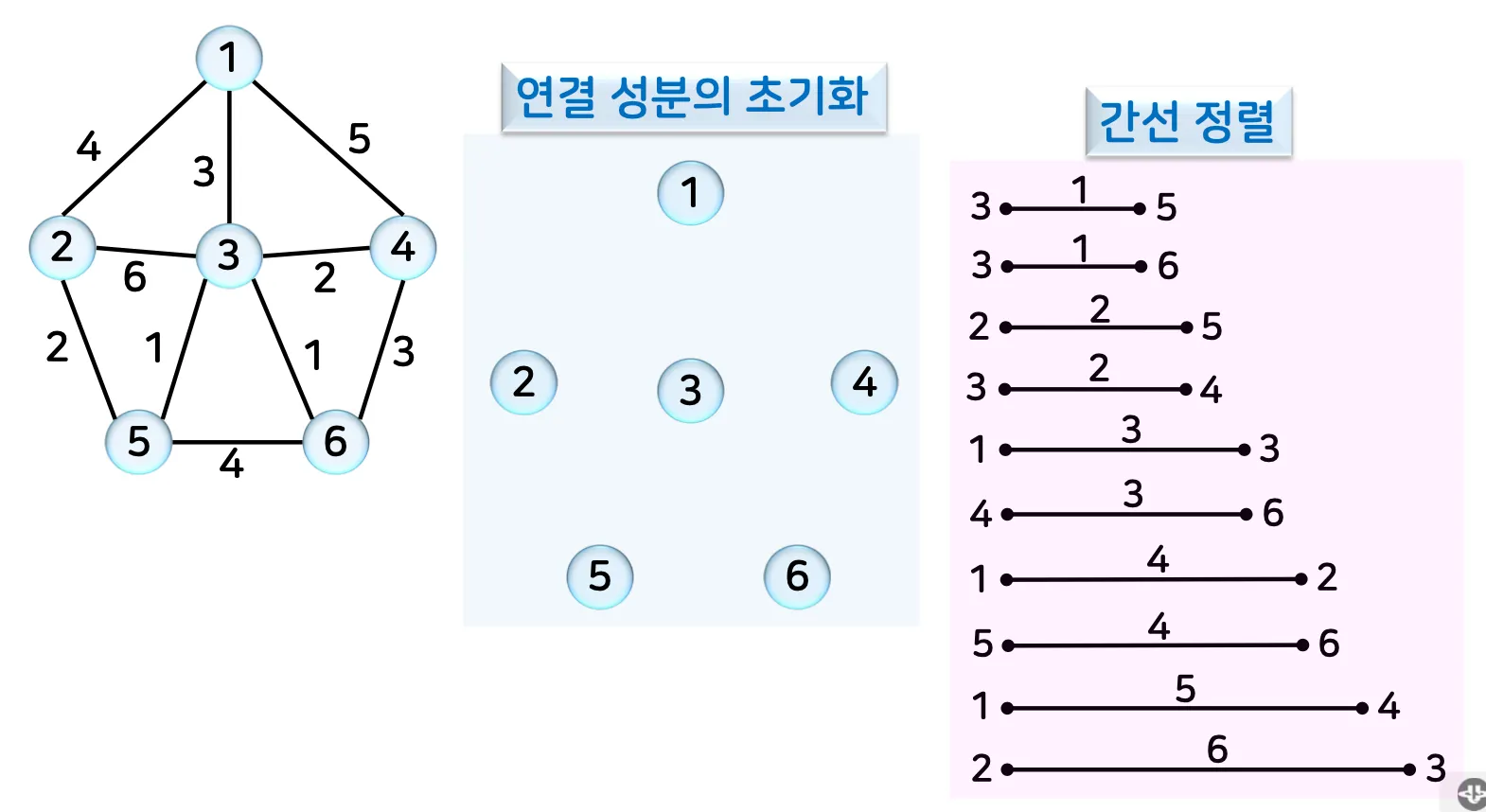
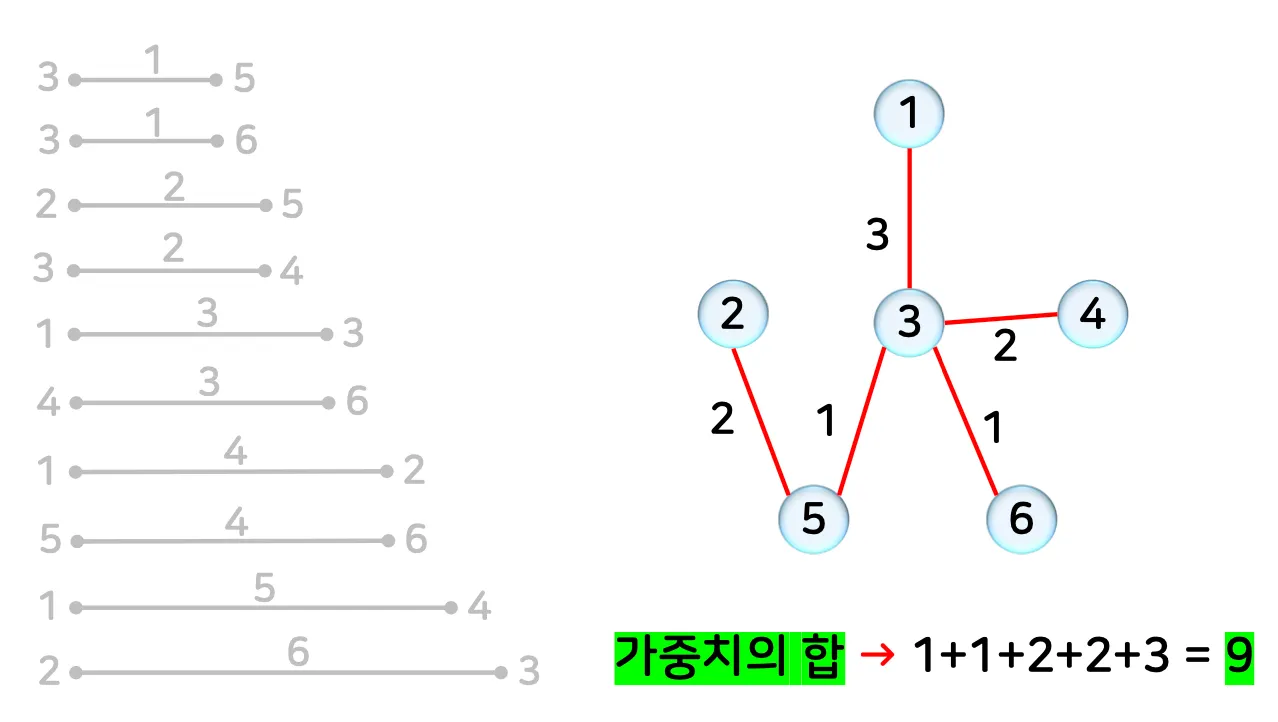
•
동작 원리
1.
그래프의 모든 간선을 가중치 오름차순으로 정렬
2.
가중치가 가장 작은 간선을 선택
3.
선택한 간선이 사이클을 형성하지 않는다면 트리에 추가
4.
트리에 모든 간선이 추가될 때까지 반복
•
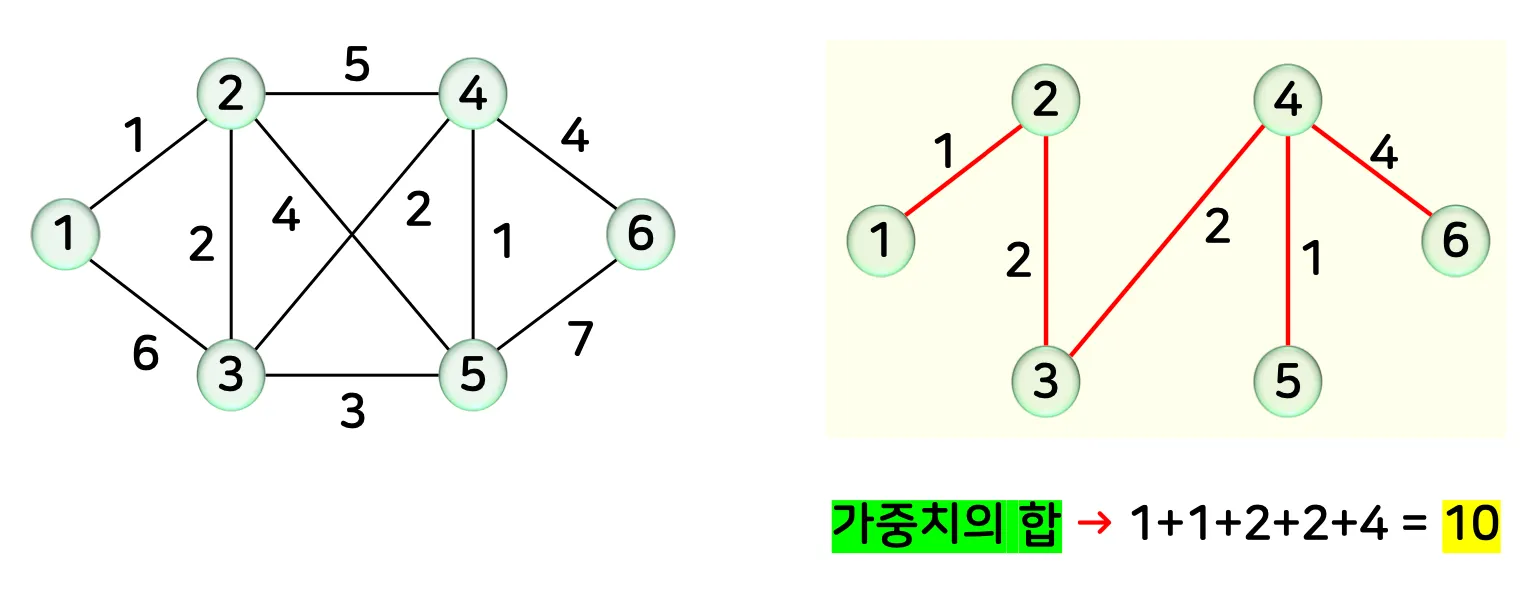
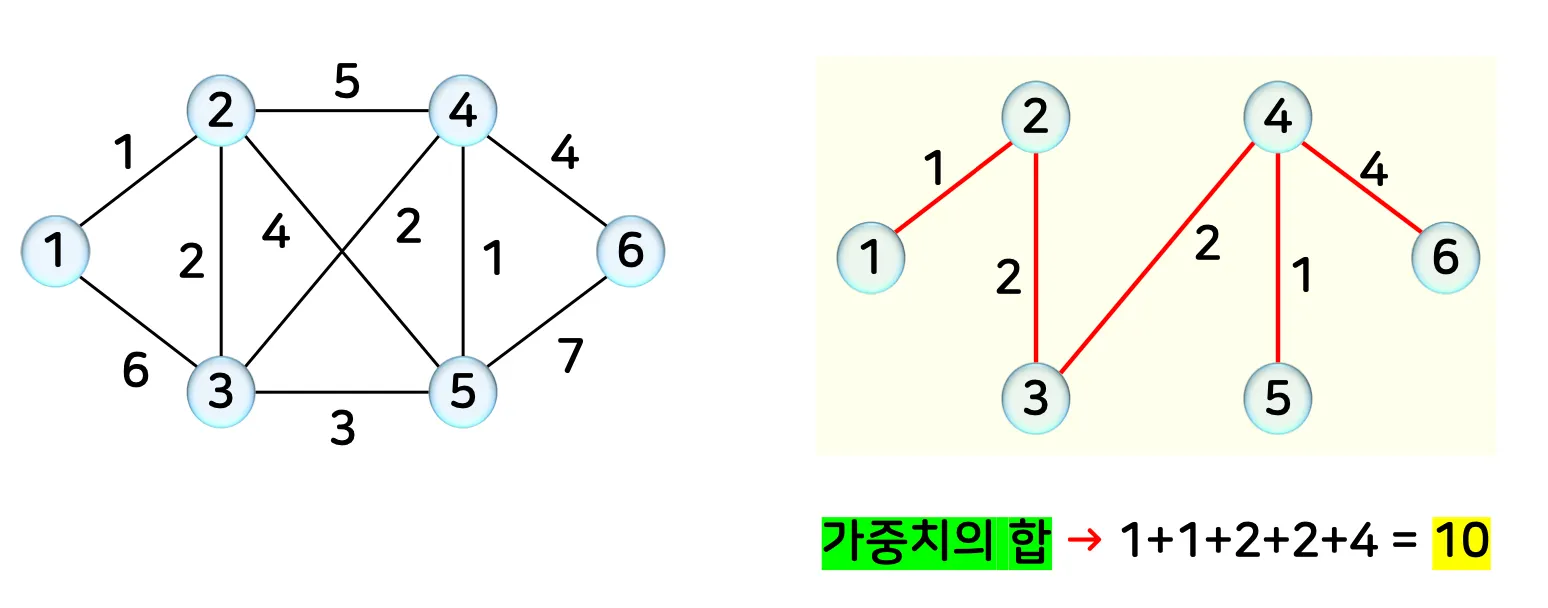
예시 1)
•
예시 2)
2.2. 예시 코드
Kruskal ( G )
{
T = Ø;
for ( G의 각 정점 v에 대해 )
정점 v로 구성된 연결 성분 초기화;
가중치가 증가하는 순으로 모든 간선을 정렬;
for ( 가중치가 가장 작은 간선부터 모든 간선 (u, v)∈E에 대해서 )
if ( u와 v가 서로 다른 연결 성분에 속하면 ) { // 사이클을 형성하지 않으면
T = T ∪ { (u, v) };
u가 속한 연결 성분과 v가 속한 연결 성분을 합침;
}
else 간선 (u, v)를 버림;
return (T);
}
C
복사
# Union-Find (Disjoint Set) 자료구조 구현
class UnionFind:
def __init__(self, n):
# 초기에는 자기 자신이 루트
self.parent = list(range(n))
# (선택사항) 트리 높이를 최소화하기 위한 rank 배열
self.rank = [0] * n
def find(self, x):
# x의 루트를 찾는 함수 (경로 압축(Path Compression) 기법 사용)
if self.parent[x] != x:
self.parent[x] = self.find(self.parent[x])
return self.parent[x]
def union(self, a, b):
# a와 b가 속한 집합을 합치는 함수
rootA = self.find(a)
rootB = self.find(b)
if rootA != rootB:
# rank가 낮은 쪽을 rank가 높은 쪽에 붙인다.
if self.rank[rootA] < self.rank[rootB]:
rootA, rootB = rootB, rootA
self.parent[rootB] = rootA
if self.rank[rootA] == self.rank[rootB]:
self.rank[rootA] += 1
return True
return False
def kruskal(nodes, edges):
"""
nodes: 정점 목록 (예: [0, 1, 2, 3] 또는 range(n))
edges: (u, v, w)의 튜플로 이루어진 리스트 -> u, v는 정점, w는 가중치
return: (mst_edges, total_weight)
"""
# 1. 간선을 가중치 기준으로 오름차순 정렬
edges.sort(key=lambda x: x[2])
# 2. Union-Find 구조 초기화
uf = UnionFind(len(nodes))
mst_edges = []
total_weight = 0
# 3. 가중치가 작은 간선부터 확인하여, 사이클이 생기지 않으면 MST에 추가
for u, v, w in edges:
if uf.union(u, v): # 두 정점이 합쳐지면(= 사이클이 없다면)
mst_edges.append((u, v, w))
total_weight += w
return mst_edges, total_weight
if __name__ == "__main__":
# 예시: 정점이 0~5번, 6개 정점이라 하자
nodes = [0, 1, 2, 3, 4, 5]
# (u, v, w) 형태의 간선들
edges = [
(0, 1, 4), # 정점 0과 1이 가중치 4로 연결
(0, 2, 4),
(1, 2, 2),
(2, 3, 3),
(2, 5, 2),
(2, 4, 4),
(3, 4, 3),
(4, 5, 3),
]
mst, total = kruskal(nodes, edges)
print("MST에 포함된 간선:", mst)
print("MST의 총 가중치:", total)
Python
복사
2.3. 성능
•
시간 복잡도: O(Elog E)
3. 프림 알고리즘
3.1. 개념
•
정의
◦
임의의 한 정점에서 시작해서 연결된 정점을 하나씩 선택해 나가는 방법
•
동작 원리
1.
임의의 정점을 선택하여 시작
2.
어떤 순간에 이미 선택된 정점의 집합 S와 선택되지 않은 정점 집합 V-S 를 잇는 간선 중에서 가중치가 가장 작은 간선을 선택
3.
간선이 연결하는 정점을 S에 추가
4.
S = V가 될 때까지 반복
•
예시
3.2. 예시 코드
Prim ( G )
{
T = ∅;
S = { 1 }; // 임의의 정점(예, 여기서는 1)으로 초기화
while ( S != V ) {
u ∈ S, v ∈ V-S인 것 중 가중치가 최소인 간선 (u, v) 선택;
T = T ∪ {(u, v)};
S = S ∪ { v };
}
return ( T );
}
C
복사
import heapq
def prim(graph, start=1):
"""
graph: 딕셔너리 형태의 인접 리스트
예)
graph = {
1: [(가중치, 2), (가중치, 3), ...],
2: [(가중치, 1), (가중치, 4), ...],
...
}
start: 초기 정점(기본값 1)
return: (mst_edges, total_weight)
mst_edges: MST에 포함된 (u, v, cost) 튜플의 리스트
total_weight: MST 전체 가중치
"""
visited = set([start]) # 집합 S를 나타냄 (초기에는 start만 포함)
edges = [] # (가중치, u, v) 형태로 우선순위 큐에 저장
mst_edges = [] # MST에 포함되는 간선들
total_weight = 0
# 시작 정점(start)와 인접한 모든 간선을 우선순위 큐에 삽입
for cost, nxt in graph[start]:
heapq.heappush(edges, (cost, start, nxt))
# 모든 정점이 방문될 때까지 반복
while len(visited) < len(graph):
# 가장 가중치가 작은 간선을 추출
cost, u, v = heapq.heappop(edges)
# 이미 방문한 정점이라면 스킵(사이클 방지)
if v in visited:
continue
# 새로 방문할 정점 v를 MST에 포함
visited.add(v)
mst_edges.append((u, v, cost))
total_weight += cost
# 새로 방문한 정점 v와 연결된 간선을 우선순위 큐에 추가
for nxt_cost, nxt_node in graph[v]:
if nxt_node not in visited:
heapq.heappush(edges, (nxt_cost, v, nxt_node))
return mst_edges, total_weight
if __name__ == "__main__":
# 예시 그래프 (정점: 1 ~ 5)
# 각 정점에 대해 (간선 가중치, 연결된 정점) 형태의 리스트
graph = {
1: [(4, 2), (3, 3), (2, 4)],
2: [(4, 1), (1, 3), (5, 5)],
3: [(3, 1), (1, 2), (2, 5)],
4: [(2, 1), (7, 5)],
5: [(5, 2), (2, 3), (7, 4)]
}
mst, total = prim(graph, start=1)
print("MST에 포함된 간선:", mst) # (u, v, cost) 형태의 리스트
print("MST 전체 가중치:", total)
Python
복사
3.3. 성능
•
시간 복잡도
◦
인접 행렬의 경우 O(|V|^2)
◦
인접 리스트 + 힙을 사용한 경우 (우선순위 큐 활용) O((|V| + |E|) log |V|)